欧拉公式的适用范围。欧拉公式是根据曲线近似微分方程导出的，应用此微分方程时，材料必须服从胡克定律。因此，欧拉公式的适用范围应当是压杆的临界应力σcr，不超过材料的比例极限σP，即λP为压杆的临界应力达到材料的比例极限时的柔度值，即则欧拉公式的适用范围为式（9-5）表明，当压杆的柔度λ 不小于λP 时，才可以应用欧拉公式计算临界力或临界应力。这类压杆称为大柔度杆或细长杆，欧拉公式只适用于较细长的大柔度杆。......
2025-09-29
结构力学：无剪力分配法的应用及适用条件
【摘要】：无剪力分配法是计算符合某些特定条件的有侧移刚架的一种方法，如前所述，力矩分配法只能用于无侧移结构，也就是说该方法只能应用于计算只有结点转角位移的结构。对于剪力静定的结构，它的侧移可以不作为未知量，因此这种结构足可以用力矩分配法计算的，称为无剪力分配法。图8-12 对无剪力分配法的应用要注意以下两点：要注意适用条件，如对图 8-13 所示的有侧移刚架是不能使用无剪力分配法的。
无剪力分配法是计算符合某些特定条件的有侧移刚架的一种方法，如前所述，力矩分配法只能用于无侧移结构，也就是说该方法只能应用于计算只有结点转角位移的结构。对于剪力静定的结构，它的侧移可以不作为未知量，因此这种结构足可以用力矩分配法计算的，称为无剪力分配法。下面通过一个例题来说明具体的解题方法和过程。
【例题8-5】 试利用对称性用力矩分配法计算图 8-10（a）所示刚架，并绘出弯矩图。
解：此刚架荷载并非对称，为了利用对称性来计算，可将荷载分解为对称的和反对称的两个部分，如图 8-10（b）和（c）所示，现分别计算如下。
（1）在对称荷载作用下的计算［见图 8-10（b）］。
在对称荷载作用下，处于对称轴上梁中点截面，剪力等于零，且无角位移和水平线位移。取出半边刚架来计算，则另一半刚架对其所起的约束作用，可简化为定向支座，如图 8-11（a）所示。
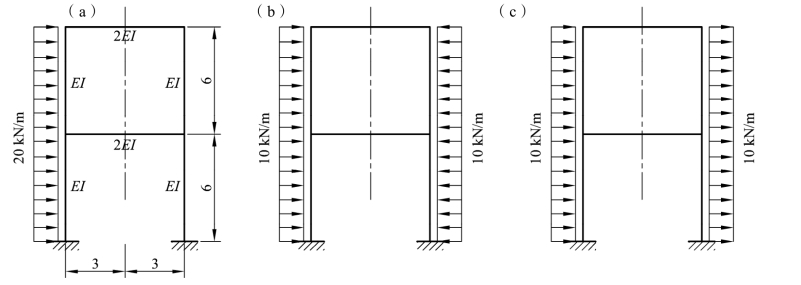
图8-10
① 计算弯矩分配系数。
② 计算固端弯矩，由图 8-11（b）所示的荷载产生的固端弯矩，得
此时，刚结点 B 和刚结点 C，由荷载产生的不平衡力矩分别为：
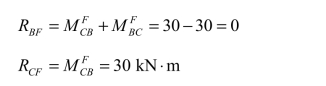
③ 弯矩的分配与传递。
弯矩的分配与传递的过程列表计算如下（见表 8-1）。
表8-1
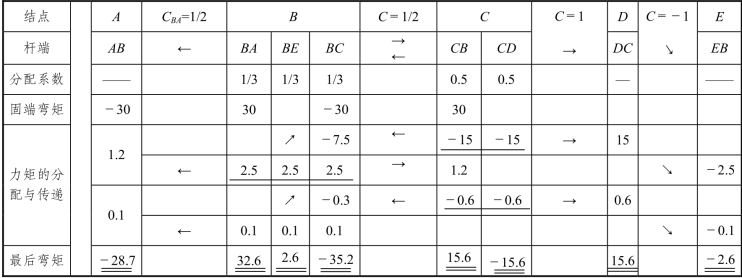
根据表内的计算结果，可作出刚架在对称荷载作用下所产生的弯矩图，如图 8-12（a）所示。
（2）在反对称荷载作用下的计算［见图 8-10（c）］。
在反对称荷载作用下，处于对称轴上的横梁中点截面，弯矩和轴力均等于零，且无竖向位移。如取出半边刚架来计算，则另一半刚架对其所起的约束作用，可简化为铰支座，如图8-11（c）所示。
图8-11(https://www.chuimin.cn)
此时，刚架也有两个刚结点。同时，刚结点 B 和 C 都有水平移动，横梁 CD、BE 虽有水平位移，但两端并无相对线位移，这称为无侧移杆件，竖柱 AB、BC 两端虽有相对侧移，但由于支座 D、E 处无水平反力，故 AB、BC 柱的剪力是静定的，这称为剪力静定杆。因此，柱顶的水平位移不作为未知量，而把每层柱子看成是下端固定、上端为定向支座的单跨超静定梁，如图 8-11（e）所示。因此，这样就只有两个刚结点的角位移未知量，便于用力矩分配法来计算了。
基本结构是在刚结点 B 和刚结点 C 上，分别设置附加刚臂约束，如图 8-11（d）所示。
由于在反对称荷载作用下，半刚架的支承情况与前面对称荷载时不同，所以分配系数要重新计算。各杆的线刚度由前可知为 iAB=iBC= i，iBE=iCD= 4i 。分配系数计算如下：
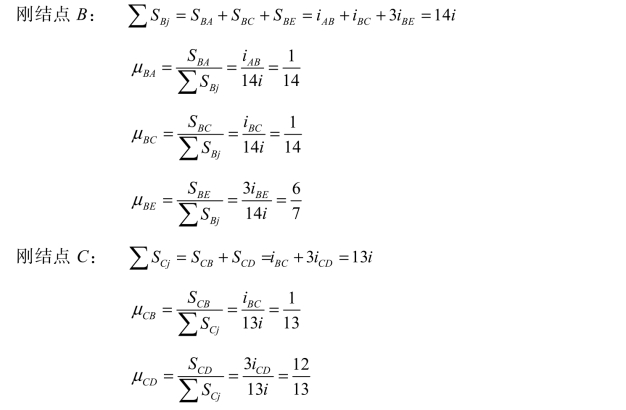
由图 8-11（d）可计算荷载产生的固端弯矩，上层柱 BC，按下端固定、上端为定向支座处理，其固端弯矩可根据表 7-1 中的公式计算。
下层柱 AB，也按下端固定、上端为定向支座处理。其固端弯矩包括两个部分：一部分由直接作用在该柱上的底层横向水平均布荷载所产生的，计算方法与上相同；另一部分是由该层以上所有水平荷载的合力F = ql= 10 × 6 =60 kN所产生的，按表 7-1 中的公式（令a =l ，b=0）计算。故得
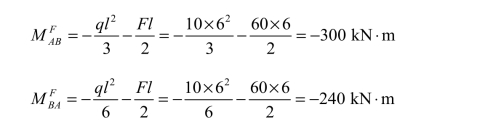
此时，刚结点 B 和刚结点 C，由荷载产生的不平衡力矩分别为：
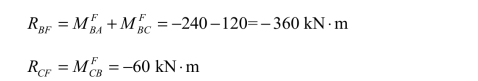
为清楚起见，也将计算过程列成表格的形式，如表 8-2 所示。不过，这时需要注意的是，柱子上、下端之间的传递系数均为Cij=Cji=-1 。
表8-2
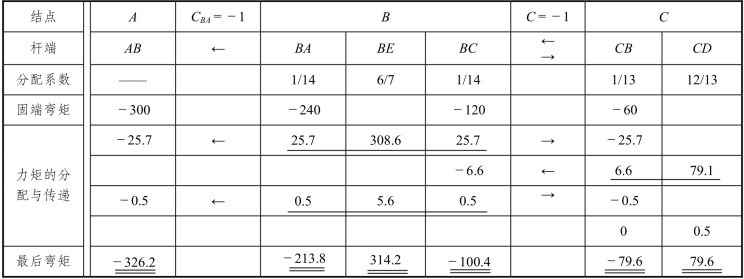
根据表内的计算结果，可作出刚架在反对称荷载作用下所产生的弯矩图，如图8-l2（b）所示。
最后，将对称荷载作用下的弯矩图［见图 8-12（a）］和反对称荷载作用下的弯矩图［见图 8-l2（b）］进行叠加，即得上述刚架在原非对称荷载作用下的弯矩图，如图8-12（c）所示。
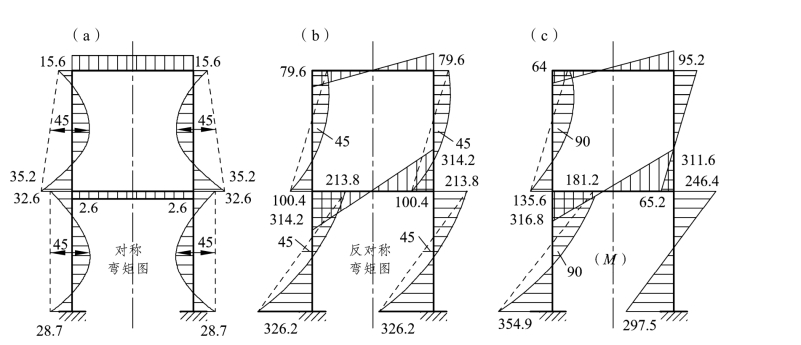
图8-12 （单位kN ·m ）
对无剪力分配法的应用要注意以下两点：
（1）要注意适用条件，如对图 8-13 所示的有侧移刚架是不能使用无剪力分配法的。这是因为，虽然柱子 AB、CD 是有侧移的，但是它们的剪力不是静定的，因此不符合无剪力分配法的应用条件。
（2）对于有侧移杆件的固端弯矩计算，作用在上一层的荷载对下一层是有影响的。
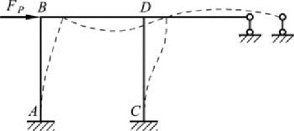
图8-13
相关文章
- 详细阅读
-
合同法：情事变更原则及适用条件详细阅读
凡是某项事态在合同成立时已预见到，则表明当事人愿意承担情事变更的风险，因此不适用情事变更原则。但是，在合同履行期限届满前合同关系已经消灭，则不能适用情事变更原则；如果部分未履行，仅就未履行部分适用情事变更原则。当事人主张适用情事变更原则，应证明情事变更非因自己的主观过错所致。......
2025-09-29
-
单结点结构的弯矩分配法-结构力学技巧详细阅读
以上两种情况叠加即为结构的实际受力状态，将第一步中各杆端的固端弯矩分别和第二步中的各杆端分配弯矩以及传递弯矩叠加，可得该结点各杆的近端或远端的最后弯矩。......
2025-09-30
-
颜色信息的作用及应用条件分析详细阅读
因此，要想利用颜色信息来提高纹理图像的识别精度，必须保持光源的颜色不发生显著变化，只有在这种条件下颜色信息对纹理图像的识别才具有积极作用。......
2025-09-29
- 详细阅读
-
力矩分配法计算无节点线位移的结构详细阅读
力矩分配法适用于计算无节点线位移的刚架和连续梁。这样的状态称为一个力矩分配单元。 用力矩分配法计算图1.8-6所示结构。图1.8-7 图1.假定当L1=6m，L2=8m，L3=5m，该梁弯矩分配系数μBA及B支座的不平衡弯矩ΔM应与下列（ ）组数据相近。C支座左右两端分配系数为0.4，0.6；固端弯矩为150kN·m、-120kN·m，试问该梁进行二次弯矩重分配，B、C支座的弯矩接近（ ）组数据。......
2025-09-30
-
LED光度测量的适用条件与要求详细阅读
参考LED集成在测量装置中，并工作于恒流和恒温状态。应注意参考LED必须与被测LED具有相同的光谱和空间分布。随后在光度测量中，根据测得的VF和上述关系的反关系求得光度测量中的实际温度。事实上，实际应用中LED典型的工作温度通常高于60℃，使光效能降低。......
2025-09-29
-
分磁环的工作原理及应用探析详细阅读
衔铁的振动既会产生噪声，又会使电磁系统以及与之刚性连接的零部件加速损坏，甚至它还有可能导致开关电器的触头发生振动，加重触头的电气磨损，引起触头熔焊，最终破坏开关电器的正常工作。因此，必须采取适当的技术措施防止电磁系统发生这种有害振动。这种导体环起到将磁通分相的作用，故称为分磁环，又由于此环系短接且电阻甚小，故又称为短路环。图4-30磁环及工作气隙的等效磁路图有分磁环时的磁极；气隙部分的等效磁路......
2025-09-29
相关推荐