以上两种情况叠加即为结构的实际受力状态，将第一步中各杆端的固端弯矩分别和第二步中的各杆端分配弯矩以及传递弯矩叠加，可得该结点各杆的近端或远端的最后弯矩。......
2023-08-30
用弯矩分配法迅速计算多结点结构
【摘要】：上面以单结点结构说明了力矩分配法的基本原理。在力矩分配法中则是逐次地将各结点轮流放松来达到同样的目的。在用弯矩分配法计算时，也只需相应设置三个附加刚臂约束。轮流放松各结点进行力矩分配和传递时，为了使计算时收敛较快，分配宜从不平衡力矩数值较大的结点开始，本例先放松结点 B。 用弯矩分配法计算图8-7 所示的超静定刚架，并作弯矩图，EI 为常数。
上面以单结点结构说明了力矩分配法的基本原理。对于具有多个结点转角但无结点线位移（或称无侧移）的结构，只需依次对各结点使用上节所述方法便可求解。做法是：先将所有结点固定，计算各杆固端弯矩；然后将各结点轮流地放松，即每次只放松一个结点，其他结点仍暂时固定，这样把各结点的不平衡力矩轮流地进行分配、传递，直到传递弯矩小到可略去时为止，以这样的逐次渐近方法来计算杆端弯矩。下面结合具体例子来说明。
图 8-5（a）所示连续梁，有两个结点转角而无结点线位移。现将两个刚结点 B、C 都固定起来，可算得各杆的固端弯矩为：
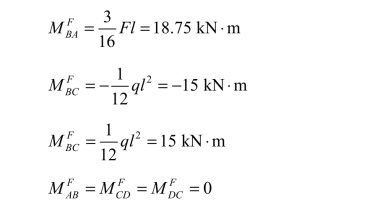
将上述各值填入图 8-5（b）的固端弯矩M F一栏中。此时结点 B、C 上各有不平衡力矩：
为了消除不平衡力矩，在位移法中是令结点 B、C 同时产生与原结构相同的转角，也就是同时放松两个结点，让它们一次转动到实际的平衡位置。如前所述，这需要建立联立方程并求解。在力矩分配法中则是逐次地将各结点轮流放松来达到同样的目的。
首先放松结点 C，此时结点 B 仍固定，故与上节放松单个结点的情况完全相同，因而可按前述力矩分配和传递的方法来消除 C 结点的不平衡力矩。为此，需先求出结点 C 处各杆端的分配系数，由于各跨EI、l 均相同，故线刚度均为i，由公式（8-5）有
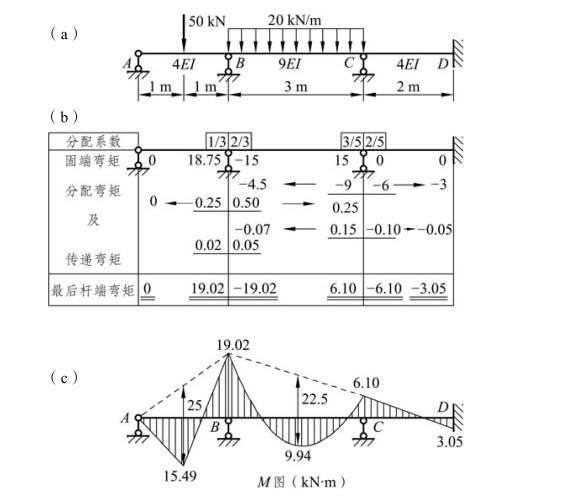
图8-5
将其填入图 8-5（b）的分配系数一栏中。把结点 C 的不平衡力矩15 kN ·m 反号并进行分配，得分配弯矩为：
把它们填入图 8-5（b）表中。这样，结点 C 便暂时获得了平衡，在分配弯矩下面画一条横线来表示平衡。此时，结点 C 也就随之转动了一个角度（但还没有转到最后位置）。同时，分配弯矩应向各自的远端进行传递，传递弯矩为：
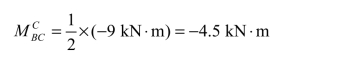
在图中用箭头表示把它们分别传递到各远端。
其次，结点 B 原有不平衡力矩3.75 kN · m，又加上结点 C 传递来的弯矩 -4.5 kN · m ，因此，共有不平衡力矩 -0.75 kN · m 。现在把结点 C 在刚才转动后的位置上重新设置附加刚臂将其固定，然后放松结点 B，于是又与上节放松单个结点的情况相同。结点 B 各杆端的分配系数为：
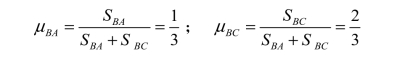
将不平衡力矩 -0.75 kN · m 反号并进行分配：
同时向各远端进行传递：
于是结点 B 亦暂告平衡，同时也转动了一个角度（也未转到最后位置），然后将它也在转动后的位置上重新固定起来。
再看结点 C，它又有了新的不平衡力矩0.25 kN ·m ，于是再又将结点 C 放松，按同样方法进行分配和传递，如此反复地将各结点轮流地固定、放松，不断地进行力矩的分配和传递，则不平衡力矩的数值将愈来愈小（因为分配系数和传递系数均小于1），直到传递弯矩的数值小到按计算精度的要求可以略去时，便可停止计算。这时，各结点经过逐次转动，也就逐渐逼近了其最后的平衡位置。
最后，将各杆端的固端弯矩和屡次所得到的分配弯矩和传递弯矩叠加起来，便得到各杆端的最后弯矩。结果见于图中的双划线之上，由此可作出弯矩图，如图 8-5（c）所示。
【例题8-3】 试用力矩分配法作图 8-6（a）所示连续梁的弯矩图。
解：此连续梁用位移法求解时有三个基本未知量，即 B、C、D 结点的角位移。在用弯矩分配法计算时，也只需相应设置三个附加刚臂约束。右边悬臂部分的内力是静定的，若将其切去，而以相应的弯矩－40 kN·m 和剪力 20 kN 作为外力施加于结点 E 处，则结点 E 便化为铰支端来处理。
（1）计算弯矩分配系数。
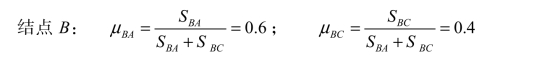
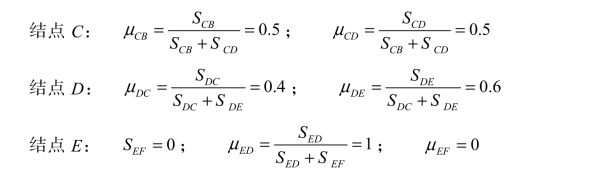
将分配系数分别写于图 8-6（b）中方框内。
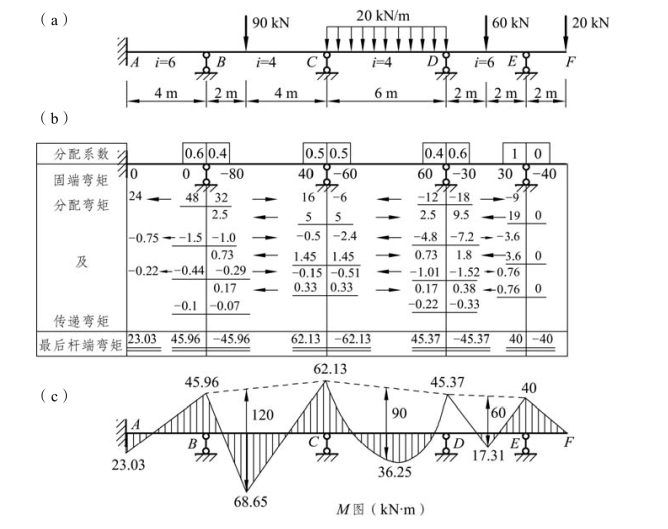
图8-6
（2）计算固端弯矩。
将计算结果填在图 8-6（b）中第一行。
（3）按先 B、D 后 C、E 的顺序，依次在结点处进行力矩分配与传递，并把分配和传递弯矩写于杆端，将历次分配和传递弯矩叠加求得各杆端的最后弯矩，如图 8-6（b）所示。
（4）根据杆端最后弯矩，用叠加法作弯矩图，如图 8-6（c）所示。
轮流放松各结点进行力矩分配和传递时，为了使计算时收敛较快，分配宜从不平衡力矩数值较大的结点开始，本例先放松结点 B。此外，由于放松结点 B 时 C 结点是固定的，故又可同时放松结点 D。由此可知，凡不相邻的各结点每次均可同时放松，这样便可加快收敛的速度。整个计算详见图 8-6（b）。
【例题8-4】 用弯矩分配法计算图8-7 所示的超静定刚架，并作弯矩图，EI 为常数。
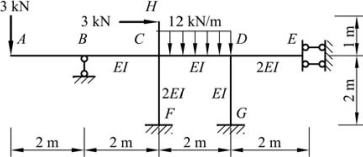
图8-7
解：该结构含有静定部分，因此首先将原结构简化为图 8-8（a）所示结构，然后计算分配系数及固端弯矩，再进行分配和传递。
（1）求分配系数（设EI=1）。
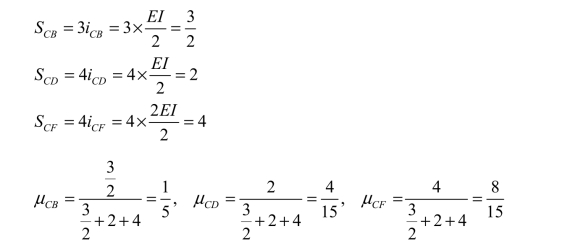
同理
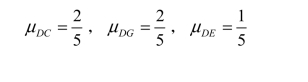
（2）求固端弯矩。
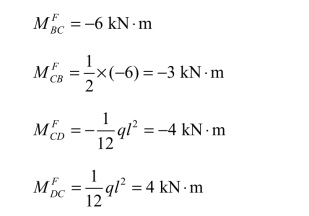
（3）弯矩的分配与传递。
按 C、D 顺序进行分配，RCF＝－3－3－4＝－10 kN·m，RDF＝4 kN·m，为缩短计算过程，应先放松约束力矩较大的结点 C。分配及传递的计算过程详见图 8-8（b）。
（4）绘制最终弯矩图。
根据叠加原理计算各杆端弯矩，绘制出弯矩图，如图 8-8（c）所示。
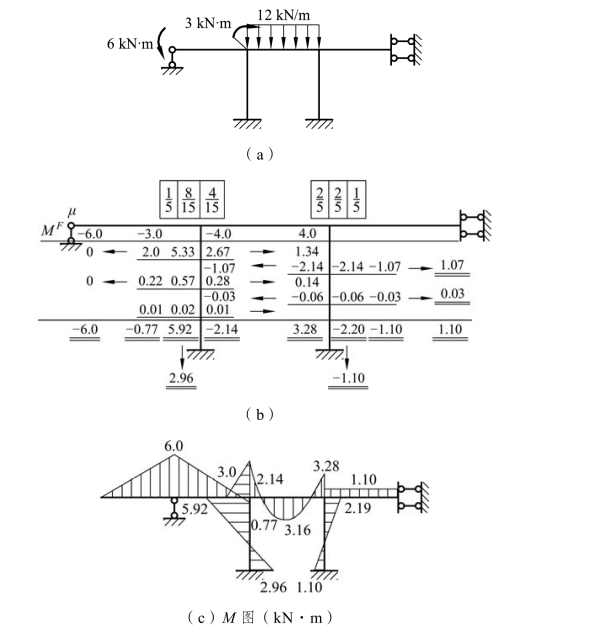
图8-8
【例题8-5】 用力矩分配法作图 8-9（a）所示封闭框架的弯矩图。EI 为常数。
解：图 8-9（a）所示刚架，结构和荷载对两个轴都是对称的。在对称轴 x 上的 C、D 点只有水平位移，而没有竖向位移和转角；在对称轴 y 上的 A、B 点只有竖向位移，而没有水平位移和转角。因此，可取结构的四分之一进行计算，对称轴上的点可取为滑动支座。计算简图如图 8-9（b）所示。作出该部分弯矩图后，其余部分根据对称结构承受对称荷载作用，弯矩图亦应是对称的关系，便可作出结构的弯矩图。
（1）计算分配系数，只有一个结点 C。
转动刚度：
分配系数：
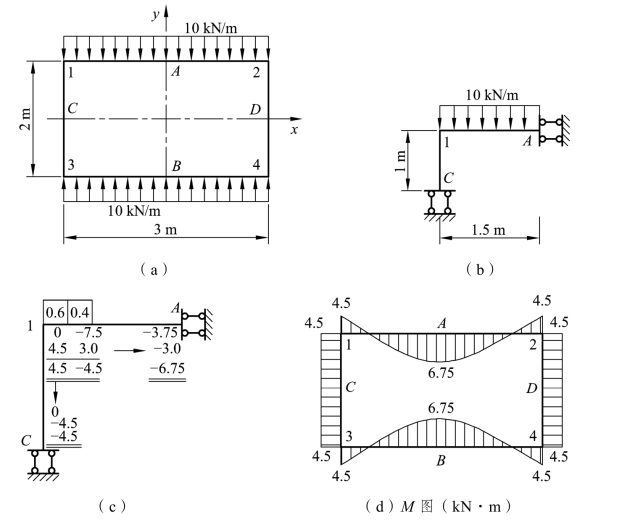
图8-9
（2）计算固端弯矩。
由表 7-1 得各杆的固端弯矩为：
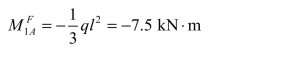
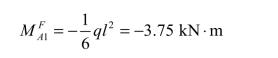
（3）进行力矩的分配和传递，求最后杆端弯矩，计算过程如图 8-9（c）所示。
（4）作弯矩图。根据对称关系作出弯矩图，如图 8-9（d）所示。
有关结构力学的文章
- 详细阅读
- 详细阅读
-
如何计算有结点线位移的结构？详细阅读
如果结构的结点有线位移，则称为有结点线位移结构。用位移法计算有结点线位移结构时，基本步骤与计算无结点线位移结构相同，其区别在于：在基本未知量中，含有结点线位移，故在写转角位移方程时要考虑线位移的影响。此刚架有一个刚结点B，其转角位移记作φB；有一个线位移，记作Δ，如图15-9所示。利用刚性结点的力矩平衡条件和产生线位移层的截面力平衡条件，建立位移法方程。......
2023-06-16
-
结构损伤多尺度模拟与分析领域变分原理详细阅读
子域泛函Π（·）可以表示为：其中，分别为Ω（·）域中的应变能密度、位移场、应变场和损伤场为分布的体力，Sσ为边界面力所作用的边界。在子域Ωnv－macro中没有损伤演化，如果再忽略材料中先天的初始损伤，则可认为该域中材料为线弹性的，因此。......
2023-08-26
-
混凝土结构设计计算-弯矩叠合图详细阅读
设计弯矩图又称弯矩包络图，其线形为二次或高次抛物线。在均布荷载作用下，简支梁的弯矩包络图一般是以支点弯矩Md、跨中弯矩作为控制点，按二次抛物线绘出。图4.11设计弯矩与抵抗弯矩叠合图图4.11中抵抗弯矩图绘制的基本方法如下：①首先在跨中截面将其最大抵抗弯矩Mu ()根据纵向主筋数量改变处的截面实有抵抗力矩分段，可近似地由各组钢筋的截面积按比例进行分段。......
2023-09-19
-
力矩分配法计算无节点线位移的结构详细阅读
力矩分配法适用于计算无节点线位移的刚架和连续梁。这样的状态称为一个力矩分配单元。 用力矩分配法计算图1.8-6所示结构。图1.8-7 图1.假定当L1=6m，L2=8m，L3=5m，该梁弯矩分配系数μBA及B支座的不平衡弯矩ΔM应与下列（ ）组数据相近。C支座左右两端分配系数为0.4，0.6；固端弯矩为150kN·m、-120kN·m，试问该梁进行二次弯矩重分配，B、C支座的弯矩接近（ ）组数据。......
2023-08-28
-
无侧移结构的位移法计算与弯矩图绘制详细阅读
只有结点角位移而无结点线位移的结构称为无侧移结构。因为只有角位移，只需建立刚结点的力矩平衡方程就可以求解出基本未知量，进而计算杆端弯矩绘制内力图。用位移法计算图15-8所示刚架，并作其弯矩图。对于具有多个结点角位移未知量的结构，可利用每个刚性结点列出一个力矩平衡方程，由于刚性结点的数目与结点角位移的数目是相同的，则所列出的位移法方程的个数与基本未知量的个数恰好相等，解联立方程即可求解出所有的基本未知量。......
2023-06-16
-
3.2结构力学：多跨静定梁的内力计算详细阅读
图3-6多跨静定梁是由若干单跨静定梁相互用铰连接起来的，通常有两种基本形式。图3-82.多跨静定梁的内力计算从受力分析来看，由于基本部分直接与地基组成几何不变体系，因此它能独立承受荷载而维持平衡。......
2023-08-30
相关推荐