以上两种情况叠加即为结构的实际受力状态,将第一步中各杆端的固端弯矩分别和第二步中的各杆端分配弯矩以及传递弯矩叠加,可得该结点各杆的近端或远端的最后弯矩。......
2023-08-30
对于结点无线位移的超静定结构,用位移法求解是为了消除基本结构各个刚结点上的附加约束反力矩,表达为联立方程的形式,通过解方程而一次完成的。用弯矩分配法计算多结点的结构时,为消除附加约束反力矩,是对每个附加约束逐次松弛、反复多次进行的,从结点被锁固的状态出发,将各结点逐次恢复转角位移的过程,直接表达为各杆端弯矩的逐次修正的过程;当松弛结束时,变形和内力趋于实际的最终状态。其计算过程的实质是松弛法求解联立代数方程的过程,各杆端弯矩逐次渐近于精确值,所以又称弯矩分配法为渐近法。
1.符号规定
弯矩分配法的理论基础是位移法,弯矩分配法中对杆端转角、杆端弯矩、固端弯矩的正负号规定与位移法相同,即假设对杆端顺时针旋转为正。作用于结点的外力偶荷载和作用于转动约束的约束力矩,也假设对结点或约束顺时针旋转为正。
2.结点力偶的分配与传递
图 8-1(a)所示为无结点线位移的单结点刚架,在 A 结点有力偶 mA作用,用位移法计算时,基本未知量为刚结点 A 的角位移 Z1,位移法方程为:

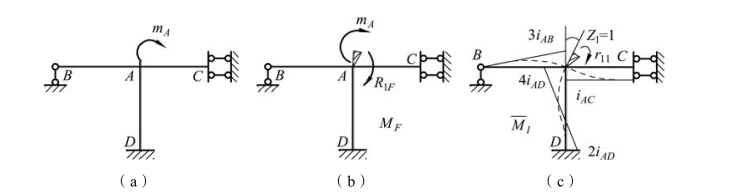
图8-1
(1)转动刚度。
通常把杆件转动的一端称为近端,另一端称为远端。
当刚结点 A 产生单位角位移 Z1=1 时,各杆近端弯矩由图 8-1(c)所示的 图有:
图有:

上式中SAB、SAC和SAD分别称为AB、AC 和AD 的近端转动刚度,它是使杆近端产生单位转角时所需施加的力矩,表示杆端对转动的抵抗能力,此值不仅与杆件的弯曲线刚度i=EI/l 有关,而且与杆件另一端(远端)的支承情况有关。图 8-2(a)、(b)、(c)分别为不同支承情况的等截面杆,相应的近端转动刚度分别为:
远端固定 SAB=4i
远端铰支 SAB=3i
远端滑动 SAB=-i
交于 A 结点各杆在A 端的转动刚度之和,称为A 结点的转动总刚度。
![]()
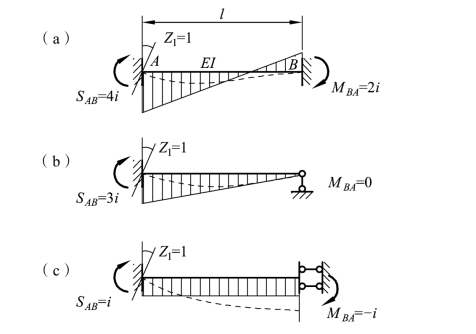
图8-2
(2)分配系数。
由图 8-1(b)所示的MF图有:
![]()
R1F是结点固定时附加刚臂约束上的约束反力矩,亦是使结点A 不平衡的力矩。
将式(c)及(d)带入位移法方程(a)式,解得

根据叠加原理,由M =M1Z1+MF,即可求出由于A 结点转动Z1时各杆端获得的弯矩。
近端弯矩:
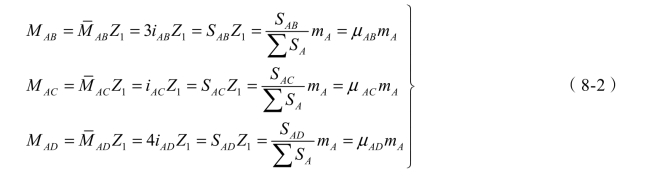
远端弯矩:

另由式(8-2)可得

式(8-5)中,μAj称为弯矩分配系数,表示 A 结点上作用的外力偶荷载mA分配到 A 结点各杆近端弯矩的比例,其中j 可以是 B、C、D 等。分配系数μAj数值上等于杆 Aj 的转动刚度与 A 结点转动总刚度的比值。显然,在同一结点上,各杆弯矩分配系数总和应等于1,即:
![]()
(3)传递系数。
结点转动时,力偶荷载mA在结点各杆近端产生分配弯矩,与此同时,杆远端亦产生弯矩,称为传递弯矩,表示为 ,由式(8-3)可知
,由式(8-3)可知
![]()
在式(8-3)中,CAj称为传递系数,表示当杆件近端转动时,杆件远端传递弯矩与近端分配弯矩的比值。由上式可得:

由上式可见,在等截面杆件中,传递系数C 随远端的支承情况而不同,图 8-2(a)、(b)、(c)所示各杆的传递系数分别为:
远端固定 C=1/2
远端铰支 C=0
远端滑动 C=-l
对于图 8-1(a)所示受结点力偶mA作用的单结点结构,结点力偶 mA将按各杆近端的分配系数进行分配,然后再按传递系数向远端传递,由此得到各杆件的杆端弯矩,不必再一步一步按位移法进行求解。这就是由位移法导出弯矩分配法的基本思想。
有关结构力学的文章

以上两种情况叠加即为结构的实际受力状态,将第一步中各杆端的固端弯矩分别和第二步中的各杆端分配弯矩以及传递弯矩叠加,可得该结点各杆的近端或远端的最后弯矩。......
2023-08-30

剪力分配法是适用于铰接排架和横梁为刚性杆、竖柱为弹性杆的有侧移刚架的计算。这种利用剪力分配系数求柱顶剪力的方法称为剪力分配法。对于图8-15 所示横梁刚度为无限大的刚架,柱顶作用水平荷载,结点角位移为零,只有一个独立结点线位移,故同样可采用剪力分配法进行计算。图8-18解:计算剪力分配系数。......
2023-08-30

上面以单结点结构说明了力矩分配法的基本原理。在力矩分配法中则是逐次地将各结点轮流放松来达到同样的目的。在用弯矩分配法计算时,也只需相应设置三个附加刚臂约束。轮流放松各结点进行力矩分配和传递时,为了使计算时收敛较快,分配宜从不平衡力矩数值较大的结点开始,本例先放松结点 B。 用弯矩分配法计算图8-7 所示的超静定刚架,并作弯矩图,EI 为常数。......
2023-08-30

据此可以判断,在荷载组中部的几个集中荷载作用的截面,发生绝对最大弯矩的可能性最大。经验表明,在通常情况下产生简支梁绝对最大弯矩时的临界荷载 FK就是使跨中截面产生最大弯矩时的临界荷载。试求简支梁的绝对最大弯矩,并与跨中截面 C 的最大弯矩相比较。包络图分为弯矩包络图和剪力包络图。......
2023-08-30

无剪力分配法是计算符合某些特定条件的有侧移刚架的一种方法,如前所述,力矩分配法只能用于无侧移结构,也就是说该方法只能应用于计算只有结点转角位移的结构。对于剪力静定的结构,它的侧移可以不作为未知量,因此这种结构足可以用力矩分配法计算的,称为无剪力分配法。图8-12 对无剪力分配法的应用要注意以下两点:要注意适用条件,如对图 8-13 所示的有侧移刚架是不能使用无剪力分配法的。......
2023-08-30

图15-352.分配系数、分配弯矩图15-36所示的刚架,由于刚结点上力偶矩mA的作用而发生变形,刚结点A发生转角θA而达到平衡。杆件AB在刚结点A的分配系数μAB等于杆体AB的转动刚度与交于A点的各杆转动刚度之和的比值。同一刚结点各杆分配系数之间存在下列关系:以上的计算可简单表述为:将作用在刚结点A上的力偶矩按各杆的分配系数直接分配于各杆的A端。远端为自由端时,近端力矩、远端力矩均等于零。故将远端弯矩称为传递弯矩。......
2023-08-26

DS域与DS区:DS域是一系列相连的DS节点构成的集合,这些节点遵循统一的服务提供策略并实现一致的PHB组。流量分类器的主要功能是依据每个数据包的DS值将其分类,以便根据SLA进行不同的调节和影射到一种或多种服务类型集合DSBA中,以在内部节点中接收不同等级的转发服务。PHB指对于某种DSBA,实际上是DiffServ网络节点给不同DSBA分配资源的方法,不同的PHB对应不同的缓冲区管理和分组调度机制。......
2023-10-18
相关推荐