将φ 乘以Boltzmann方程的两边，对整个颗粒脉动速度空间积分，获得φ 的输运方程。因此，可以通过假设颗粒的速度分布函数获得颗粒流的应力和能量通量等的表达式，或者用统计平均的办法建立各类守恒型方程来描述颗粒流的平均运动。因此，需要通过一定假设，建立泥沙颗粒相的本构关系。......
2025-09-29
直接建立基本方程的平衡条件
【摘要】：前面介绍了利用位移法基本结构来建立位移法方程。位移法典型方程实质上代表了原结构的结点和截面的平衡条件。因此，位移法方程的建立可以不通过附加约束的基本结构，而是利用杆件的物理方程［式（7-1）至式（7-4）］，直接取结点和截面一侧为隔离体的平衡条件，来建立以结点位移为未知量的位移法方程。利用等截面直杆的物理方程式（7-1）、式（7-2）及表 7-1，由跨度 l＝12 m，高 h＝6 m，可得图7-16建立位移法方程。
前面介绍了利用位移法基本结构来建立位移法方程。位移法典型方程实质上代表了原结构的结点和截面的平衡条件。因此，位移法方程的建立可以不通过附加约束的基本结构，而是利用杆件的物理方程［式（7-1）至式（7-4）］，直接取结点和截面一侧为隔离体的平衡条件，来建立以结点位移为未知量的位移法方程。现在举例说明。
【例题7-6】 用直接平衡法计算图 7-16（a）所示刚架的弯矩图。各杆线刚度均为i。
解：（1）确定基本未知量。
图示刚架有刚结点 C 的转角位移 Z1和结点 C、D 的水平线位移 Z2两个基本未知量。设Z1为顺时针方向转动，Z2向右移动。
（2）列出求各杆的物理方程。
利用等截面直杆的物理方程式（7-1）、式（7-2）及表 7-1，由跨度 l＝12 m，高 h＝6 m，可得
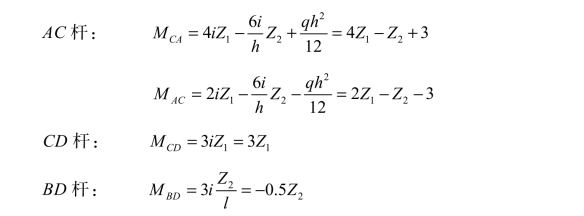
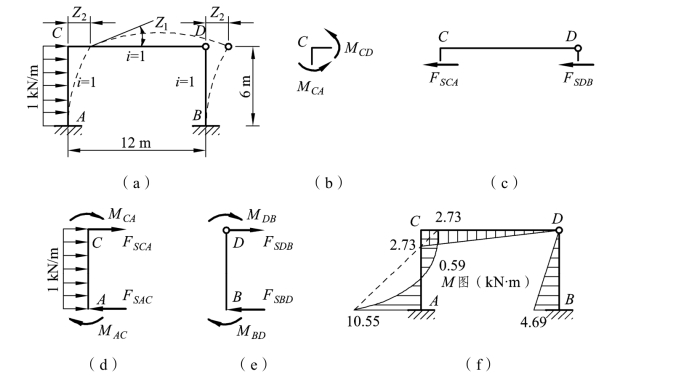
图7-16
（3）建立位移法方程。
有侧移刚架的位移法方程，有下述两种：
① 与结点转角 Z1对应的基本方程为结点 C 的力矩平衡方程，如图 7-16（b）所示，取结点 C 为隔离体，由∑MC=0，得
将 MCA、MCD代上式，经整理后得
(https://www.chuimin.cn)
② 与结点线位移 Z2对应的基本方程为横梁 CD 的截面平衡方程，如图 7-16（c）所示，取横梁 CD 为隔离体，∑Fx=0，得
取立柱 CA 为隔离体［见图 7-16（d）］，由∑MA=0，得
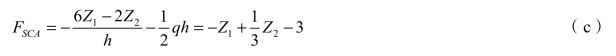
同样，取立柱 DB 为隔离体［见图 7-16（e）］，由∑MB=0，得
将（c）、（d）两式代入横梁 CD 的截面平衡方程（b）整理得
（4）将（a）、（e）两式联立得位移法方程。
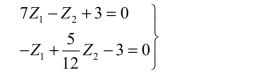
解得：
（5）计算杆端弯矩，绘制弯矩图。
将 Z1、Z2的值代入杆端弯矩表达式，求得杆端弯矩，并作弯矩图，如图 7-16（f）所示。
相关文章
- 详细阅读
-
热力计算基本方程详细阅读
冷却塔中传质和传热同时进行，冷却塔热力计算的方法目前国内外用得较多的是焓差法，这里主要介绍焓差法。a/kX=为Lewis比例系数，利用其上式可进一步简化写成：以容积传质系数kXVkg/代替kXa，填料塔微元体积dV代替Fdz，得和分别为饱和空气与微元内空气的焓，是冷却的推动力，式简称焓差方程，为冷却塔计算的基本方程式。......
2025-09-29
-
同步电机的基本方程解析详细阅读
2）隐极式同步电动机电磁功率。代入式（6.3）得从式（6.3）和式（6.4）可见，同步电机电磁功率都是θ角的正弦函数，因此θ称为功率角。将式（6.3）和式（6.4）代入上式可得：凸极式同步电动机电磁转矩隐极式同步电动机电磁转矩从式（6.5）、式（6.4）可知，同步电机转矩都是θ角的正弦函数，因此θ也称转矩角。......
2025-09-29
-
直接代数解法中的方程病态问题（Stiffne详细阅读
但是实际上，在运用直接代数解法时还需解决其带来的一些技术问题与相应的处理。首先是Stiffness问题即病态、刚性、坏条件或具有差别大的Lipsihitz问题。在液压系统特别是元件仿真中，多数场合会遇到病态问题。因此在模块式建模法的直接代数解法中，为了建立稳定的数值计算方法，着眼点是在保证精度的前提下，尽可能扩大稳定区域，使步长选择尽可能大，以达到仿真时间短，巨稳定、可靠、精度足够高的目的。......
2025-09-29
- 详细阅读
-
平衡方程的基本形式探析详细阅读
平面一般力系平衡的必要和充分条件是：力系的主矢和力系对任一点的主矩等于零。反之，如果主矢和主矩中有一个量或两个量不为零时，原力系可合成为一个合力或一个力偶，力系就不平衡，因此，主矢和主矩都等于零也是力系平衡的必要条件。由于对称性，约束力和主动力都在同一平面内。建立图示坐标系，由平面力系的平衡方程解得FB为负值，说明它的方向与假设的相反。选取恰当的坐标轴和矩心，列平衡方程。解平衡方程，求得未知量。......
2025-09-29
-
负载运行时的基本方程式优化详细阅读
变压器负载运行时，由于I0I1，故可忽略I0，这样一、二次侧的电流关系变为式表明，一、二次侧电流的大小近似与绕组匝数成反比。综前所述，将变压器负载时的基本电磁关系归纳起来，可得以下基本方程式组......
2025-09-29
-
直流电机的模型和基本方程详细阅读
直流电机模型就是由两个互相垂直的线圈组成的。图1.2 直流电机模型直流电机模型的特点如下：1）定子励磁磁动势Fs与转子磁动势Fr互相垂直（正交），从控制意义上而言，定子励磁磁动势Fs和转子磁动势Fr互相独立，可以分别控制。......
2025-09-29
相关推荐