结构力学：线位移法数目确定

2023-08-30 理论教育版权反馈

【摘要】：在确定结点线位移的数目时，由于不计受弯直杆的轴向变形，并且假设弯曲变形是微小的，即认为直杆在受弯前后其投影长度保持不变。由于在确定结点线位移数目时，不计及杆件的轴向变形和弯曲变形，因此，可以先把所有的刚性结点和固定支座全部改成铰接，使结构变成一个铰接体系。结构基本未知量的总数等于结点的角位移数和线位移数之和。

在确定结点线位移的数目时，由于不计受弯直杆的轴向变形，并且假设弯曲变形是微小的，即认为直杆在受弯前后其投影长度保持不变。在图 7-6（a）所示结构中的四个结点（结点 B、D、E、H）只有水平线位移，而且是相等的，因此，只有一个独立的线位移。

由于在确定结点线位移数目时，不计及杆件的轴向变形和弯曲变形，因此，可以先把所有的刚性结点和固定支座全部改成铰接，使结构变成一个铰接体系。用增加链杆的方法使该体系成为几何不变且无多余约束的体系，所增加的最少链杆数目，就是结点独立线位移的数目。如图 7-6（a）所示的结构，把其所有的刚性结点和固定支座改成铰接后，则变为 7-6（b）所示的铰接体系。由几何组成分析可知，该体系是几何可变的，至少需要在铰结点 H 处加一水平支杆，就能使体系成为几何不变，由此判定原结构只有一个独立的结点线位移。结构基本未知量的总数等于结点的角位移数和线位移数之和。如图 7-6（a）所示结构有三个结点角位移和一个结点线位移，共有四个位移基本未知量。

图 7-5（a）所示的刚架有 A、B、C、D 四个刚结点，即有四个角位移；图 7-5（b）为原刚架相应的铰接体系，按几何组成分析，至少要在结点 B 和 F 处加上两根水平支杆后，方可使该体系成为几何不变（杆 EF 拉压刚度 EA＝∞），所以，原结构有两个线位移，共有六个位移基本未知量。

如图 7-7（a）所示刚架，横梁 EH 的弯曲刚度 EI＝∞，在外力作用下只能平移而无转动，所以结点 E 和 H 只做水平移动而转角为零。注意，因高柱的上段和下段的刚度不同，因而把D、G 视为刚结点，因此，刚架具有结点 D 和 G 两个未知角位移。刚架的铰接体系如图 7-6（b）所示，在结点 D、G 和 H 处各加上一水平支杆，即可成为几何不变体系，所以原刚架有三个线位移，共有五个位移基本未知量。

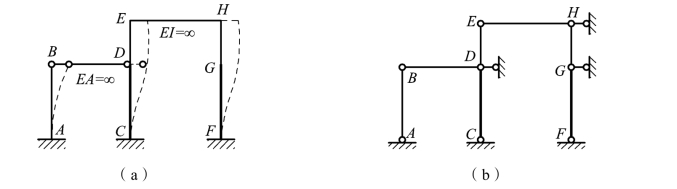
pagenumber_ebook=181,pagenumber_book=174

图7-7

需要注意的是，上述确定结点线位移数目的方法，是以不考虑受弯直杆的轴向变形为前提的。对于两力杆则必须考虑轴向变形，因此，当确定图 7-5（a）所示刚架的线位移数目时，在图 7-5（b）所示与其相应的铰接体系中，若两力杆 EF 刚度为有限值时，则还要在 C（或D 或 E）结点加上一根支杆后，才能使每个结点均不产生线位移，所以原刚架具有三个线位移，共有七个位移未知量。

结构力学：线位移法数目确定

相关推荐