确定计算简图的原则是：计算简图应尽可能反映实际结构的主要受力、变形等特性；保留主要因素，忽略次要因素，使计算简图便于分析计算。实际结构均为三维空间结构。这样，便得到如图 1-10所示的计算简图。即用图 1-12或图 1-12来计算排架结构中屋架的内力和位移，用图 1-12来计算排架结构中柱子的内力和位移。......
2023-08-30
结构力学：取半边结构的计算成果
【摘要】：对于奇数跨刚架，均可以按照上述原则取半边结构分析，以简化计算。在取半边结构计算时，全结构即刚架的中柱所承受的弯矩和剪力应为按半边结构计算时所得结果的 2 倍，而中柱的轴力因属于对称内力，两半结构叠加的结果是中柱轴力必定为零。此外，采用半边结构简化计算时，荷载必须是对称荷载或反对称荷载。
通过以上分析可知，对称结构在对称荷载作用下，内力和变形是对称的；在反对称荷载作用下，其内力和变形是反对称的。利用对称结构的这一特性，可以按照变形和内力与原结构等价的原则，先截取半边结构分析计算，然后再根据对称性得到整个结构的内力。一般来说，半边结构的超静定次数低于原结构，这样就可以使计算得到简化。以下分别以奇数跨和偶数跨的对称刚架为例，说明取半边结构的分析方法。
如图 6-26（a）所示为一单跨对称刚架，受对称荷载作用。刚架的变形和内力应是对称的，故位于对称轴上的K 截面处无水平位移和转角发生，仅可发生竖向位移；同理，K 截面处只能有弯矩和轴力而无剪力发生。因此，在取半边结构计算时，在该截面处应采用滑动支座代替原有的约束，得到如图 6-26（b）所示的计算简图，其变形和内力与原结构中的情况是相同的。
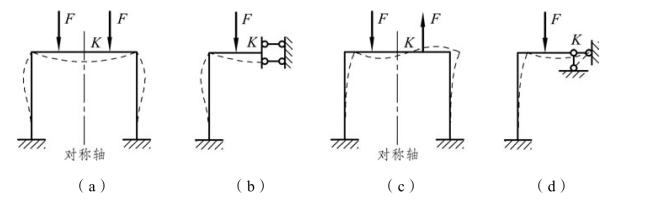
图6-26
若上述刚架受如图 6-26（c）所示的反对称荷载作用，则变形和内力应是反对称的，此时位于对称轴上的K 截面处无竖向位移发生，但可以有水平位移和转角；同理，K 截面处只能有剪力而无弯矩和轴力。因此，在取半边结构计算时，在该截面处应采用竖向链杆代替原有的约束，得到的计算简图如图 6-26（d）所示。
对于奇数跨刚架，均可以按照上述原则取半边结构分析，以简化计算。以下再讨论偶数跨的刚架。
图 6-27（a）所示为两跨对称刚架，受对称荷载作用。位于对称轴上的C 结点应无水平位移和转角发生，在忽略杆件的轴向变形后也没有竖向位移，但在C 结点两侧有弯矩、剪力和轴力存在；在取半边结构计算时，可将该处用固定支座代替，得到如图 6-27（b）所示的计算简图。此时，刚架的中柱仅受轴力作用，其数值应等于 K 处固定支座竖向反力的 2 倍。
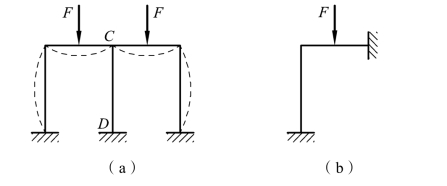
图6-27
若上述刚架受反对称荷载作用，如图 6-28（a）所示，内力和变形都是反对称的，取半刚架时，可将其中间立柱设想为由两根各具有 I/2 的立柱组成，它们分别在对称轴的两侧与横梁刚接，如图 6-28（b）所示。将其沿对称轴切开，由于荷载是反对称的，故C 截面上只有反对称的一对剪力 FSC，如图 6-28（c）所示。当忽略杆件的轴向变形时，这一对剪力 FSC对其他杆件均不产生内力，而仅在对称轴两侧的两根立柱中产生大小相等而性质相反的轴力，由于原有中间柱的内力是这两根立柱的内力之和，故剪力 FSC对原结构的内力和变形都无影响，于是可将其略去而取一半刚架的计算简图，如图 6-28（d）所示。在取半边结构计算时，全结构即刚架的中柱所承受的弯矩和剪力应为按半边结构计算时所得结果的 2 倍，而中柱的轴力因属于对称内力，两半结构叠加的结果是中柱轴力必定为零。
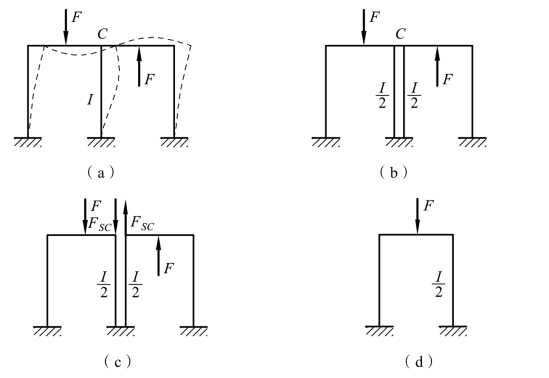
图6-28
现将对称结构的简化计算小结如下：
（1）采用对称的基本体系，将基本未知量分为对称未知力和反对称未知力两组，则在力法方程中将有 δij＝0（这里，i 为对称未知力方向，j 为反对称未知力方向）。这样，多元方程组将分解为两组低元方程。对于不同类型的荷载，又可分为三种情形：
① 对称荷载作用。则只需计算对称未知力（反对称未知力为零）。
② 反对称荷载作用。则只需计算反对称未知力（对称未知力为零）。
③ 任意荷载作用。可将其分解为对称和反对称两种情形分别计算，然后进行叠加得最后结果。也可不分解，直接用非对称荷载计算，但要采用对称的基本体系和基本未知力，力法方程自然分为两组。
（2）采用半边结构计算。对称结构可分为奇数跨和偶数跨两种情形，它们在对称荷载和反对称荷载作用时在对称轴上的变形和内力是不同的。此外，采用半边结构简化计算时，荷载必须是对称荷载或反对称荷载。 如果是非对称荷载，则须分解为对称荷载和反对称荷载两种情形，分别采用半边结构计算简图进行计算，然后叠加得最后结果。
下面举例说明半刚架法的应用。
【例题 6-9】 作图 6-29（a）所示刚架的弯矩图。
解：这是一个四次超静定的两跨对称刚架，在对称荷载作用下，其半结构的计算简图如图6-29（b）所示，此为二次超静定刚架，将刚结点 D 变为铰结点，并将固定支座E 改为铰支座，得到基本结构，如图 6-29（c）所示。其中 X1为一对大小相等的力偶，X2为支座处的反力偶。根据基本结构在多余未知力和荷载共同作用下，铰结点 D 的两侧相对转角和铰支座 E的转角应为零的变形条件，建立力法方程。
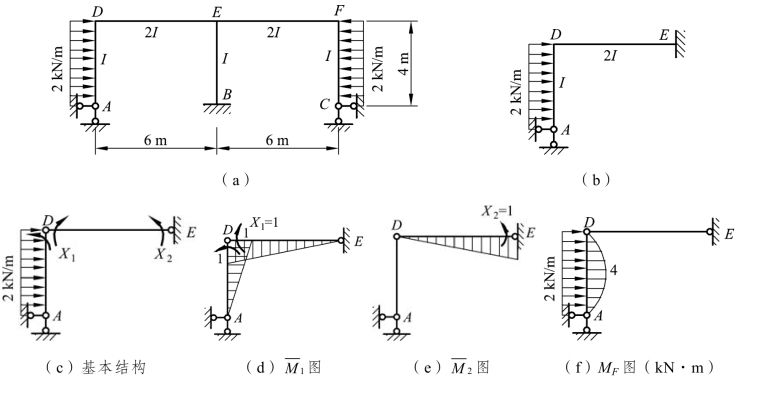
图6-29
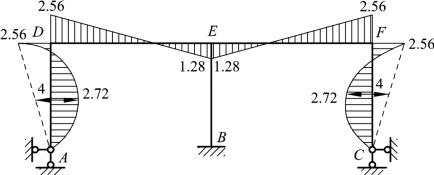
图6-30
代入力法方程解得
利用叠加公式
及M 图的对称性质, 绘制最后M 图，如图6-30 所示。
【例题6-10】 利用对称性作图 6-31（a）所示刚架的弯矩图。所有杆件的 EI 均为常数。
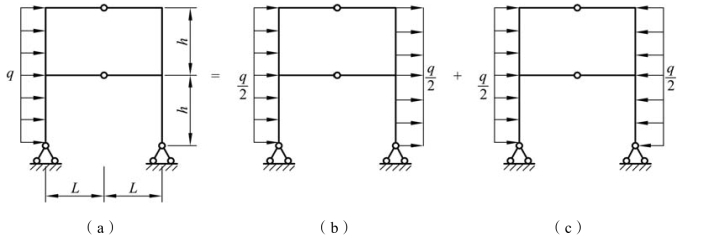
图6-31
解：该结构为对称结构，所受荷载可分解为反对称荷载与正对称荷载，如图 6-31（b）、（c）所示。
（1）反对称荷载作用下取半刚架［见图 6-32（a）］进行计算。
图6-32
① 选取基本体系。
图 6-32（a）中的半刚架为一次超静定结构，去掉一层的竖直方向支撑链杆，作用以未知反力 X1，得到图 6-32（b）所示的基本体系。
② 列出力法方程。
基本体系在多余未知力和荷载共同作用下，应满足未知力X1处竖直方向位移为零（即与原结构相同）的变形协调条件，则力法方程为：
③ 求解系数和自由项。
分别绘出基本结构在单位力X1= 1单独作用下的单位弯矩图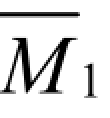
图和荷载单独作用下的弯矩图M1F图，如图 6-32（c）、（d）所示。
利用图乘法求力法方程的系数和自由项如下：
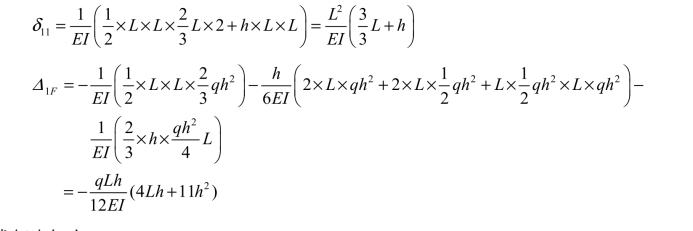
④ 求解未知力。
将上述求得的系数和自由项代入力法方程中，解得
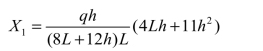
假设L＝0.8h，并代入上式化简得
⑤ 作弯矩图。
根据叠加原理：
，作出反对称荷载作用下结构的弯矩图 M ′，如图 6-34（a）所示。
（2）正对称荷载作用下，取半刚架进行计算，如图 6-33（a）所示。
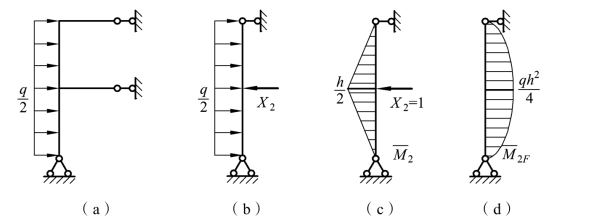
图6-33
① 选取基本体系。
图 6-33（a）中的半结构为一次超静定结构，显然两根梁的弯矩为零，去掉后得到图 6-33（b）所示的基本体系。
② 列出力法方程。
基本体系在多余未知力和荷载共同作用下，应满足未知力X2处水平方向位移为零（即与原结构相同）的变形协调条件。则力法方程为
③ 求解系数和自由项。
分别绘出基本结构在单位力X2=1单独作用下的单位弯矩图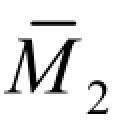
图和荷载单独作用下的弯矩图M2F图，如图 6-33（c）、（d）所示。
利用图乘法求力法方程的系数和自由项如下：
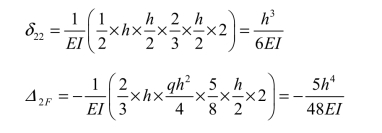
④ 求解未知力。
将上述求得的系数和自由项代入力法方程中，解得
⑤ 作弯矩图。根据叠加原理：
，作出正对称荷载作用下结构的弯矩图M′，如图 6-34（b）所示。
最后将两种情况下得到的弯矩图，即 M ′图和 M ′图叠加，得到结构的弯矩图即 M，如图6-34（c）所示。
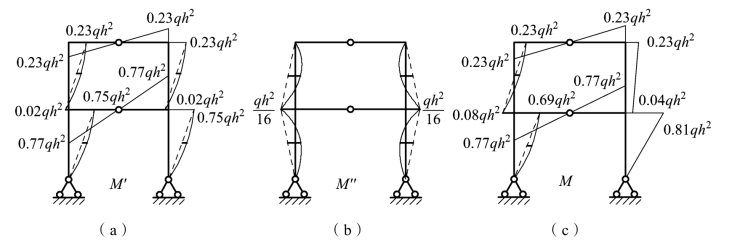
图6-34
有关结构力学的文章
- 详细阅读
-
结构力学：高效刚架计算方法详细阅读
先处理的直接刚度法计算刚架的步骤可概括如下：划分单元并对结点和单元进行编号，选取整体坐标系和单元坐标系，同时对未知结点位移和相应的结点荷载进行编码。对式（9-5)单元坐标系下的单元刚度矩阵进行坐标变换或按式直接列出各单元在整体坐标系下的单元刚度矩阵，根据变形协调条件和位移边界条件写出各单元的定位向量，进行换码。将各单元刚度矩阵中有关元素按定位向量所示非“0”的行码和列码送到结构刚度矩阵中的相应位置。......
2023-08-30
-
结构力学：组合结构与拱位移计算详细阅读
计算结果为正，表示ΔCx的方向与所设单位力的方向相同，即 ΔCx方向向右。 求图 5-17所示半圆弧三铰拱顶铰 C 两旁截面的相对转角。图5-17解：计算拱的位移，仅考虑弯矩对弯曲变形的影响，按公式计算。计算三铰拱受荷载及单位力偶作用时［见图 5-17、］的弯矩方程，应先求出支座反力，然后列出弯矩方程。此题由于三铰拱为对称结构，可只对拱的一半列出方程。......
2023-08-30
-
支座移动引起的位移计算-结构力学详细阅读
静定结构在支座移动时，只发生刚体位移，不产生内力和变形。这种位移可通过几何关系求得，也可应用单位力法进行计算。在式中，乘积的正负号规定为：当虚拟状态的支座反力与实际支座位移的方向一致时取正号，相反时取负号。 刚架的支座位移如图 5-19所示，试求 A 点的水平位移 ΔAx和 C 点左右截面的相对转角位移 θCC。......
2023-08-30
-
结构力学：温度作用下的位移计算详细阅读
在使用时，这些结构所处的环境温度相对于建造时的温度一般要发生变化，这种温度的改变将会引起构件的变形，从而使结构产生位移。对于静定结构，温度改变只会引起材料的自由膨胀、收缩，在结构中不会引起内力，但将产生变形和位移。静定结构由于温度改变引起的位移计算公式，仍可由位移计算的一般公式导出。因此，点 C 的竖向位移为计算结果为负，表示 ΔCy的方向与所设单位力的方向相反，即 ΔCy向上。......
2023-08-30
-
3.2结构力学：多跨静定梁的内力计算详细阅读
图3-6多跨静定梁是由若干单跨静定梁相互用铰连接起来的，通常有两种基本形式。图3-82.多跨静定梁的内力计算从受力分析来看，由于基本部分直接与地基组成几何不变体系，因此它能独立承受荷载而维持平衡。......
2023-08-30
-
荷载性质与分类：结构力学成果详细阅读
荷载通常是指主动作用于结构上的外力。根据荷载的分布、荷载作用时间的久暂及荷载作用的性质，可将荷载做如下分类：1.按荷载的分布划分面荷载。动力荷载是随时间迅速变化的荷载，在动力荷载作用下，结构上的质量会引起加速度和惯性力，因而引起结构显著的冲击或振动，如动力机械运转时产生的振动荷载、地震荷载、风荷载等。另外，按荷载在结构上的作用位置是否可变更来区分，又可划分为固定荷载和移动荷载。......
2023-08-30
-
结构力学：桁架多点应力应变测试及计算详细阅读
通过实验测试与理论计算结果的对比分析，验证“理想桁架”假设。根据理想桁架计算所得的内力是“主内力”，而由节点刚性等因素而引起的内力是“次内力”，在节点荷载作用下杆件内力以轴力为主，将节点简化为理想的铰接点是合理的。要求小组分工协作。考核报告质量、答辩及回答问题情况。......
2023-08-30
相关推荐