选取对称基本结构的方法

2023-08-30 理论教育版权反馈

【摘要】：我们将中间铰去掉，代之以两对多余未知力X1和X2，得到对称的基本结构，如图 6-23所示。选取对称的基本结构，切开横梁对称轴处截面，由对称性质可知，截面上对称的多余未知力为零，只需计算反对称的未知力X1，如图 6-24所示。

用力法计算对称结构时，若选取对称的基本结构，可使计算大为简化。如图 6-20（a）所示为一单跨超静定对称刚架，它有一根竖向对称轴，若在横梁上沿对称轴的截面切开，便得到一个对称的基本结构，如图 6-20（b）所示，具有三个多余未知力，基本结构在荷载及 X1、X2、X3作用下，切口两侧截面的相对转角、相对水平线位移和相对竖向线位移等于零，据此变形条件建立力法方程：

pagenumber_ebook=149,pagenumber_book=142

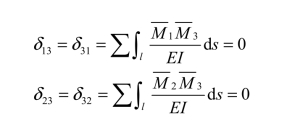
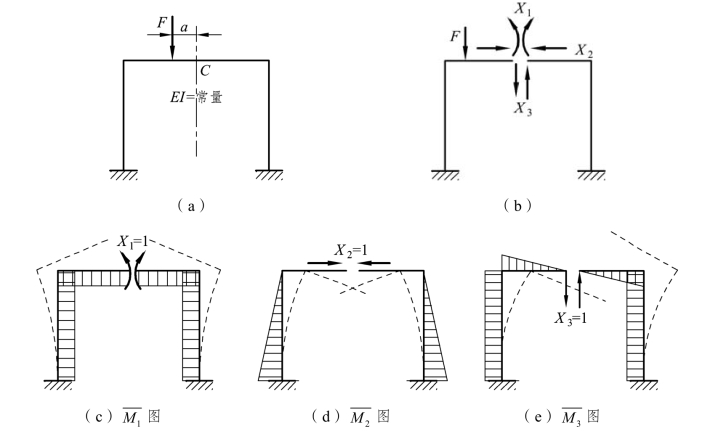
pagenumber_ebook=150,pagenumber_book=143

图6-20

于是，力法典型方程就简化为：

pagenumber_ebook=150,pagenumber_book=143

由此可见，选取对称的基本结构可将力法方程分解为两组：一组只包含正对称未知力（X1、X2），另一组只包含反对称未知力（X3），方程组降阶从而使计算大为简化。

与此同时，还可将原结构上的外荷载分组。当对称结构上作用有任意荷载时［见图6-21（a）］，可将它分解成正对称荷载［见图 6-21（b）］和反对称荷载［见图 6-21（c）］两种情况。

（1）对称荷载作用于对称结构。

在对称荷载作用下，基本结构的荷载弯矩图MF图是对称的，如图 6-22（a）所示。而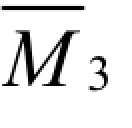 pagenumber_ebook=150,pagenumber_book=143 图是反对称的，如图 6-20（e）所示，因此

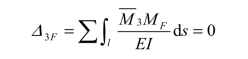
pagenumber_ebook=150,pagenumber_book=143

将上式代入力法方程式（a），可得反对称未知力X3＝0，此时力法方程简化为

pagenumber_ebook=151,pagenumber_book=144

这时只需按式（b）计算对称未知力X1和X2，如图 6-22（c）所示。

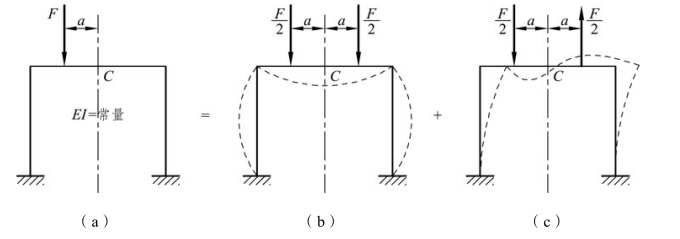
pagenumber_ebook=151,pagenumber_book=144

图6-21

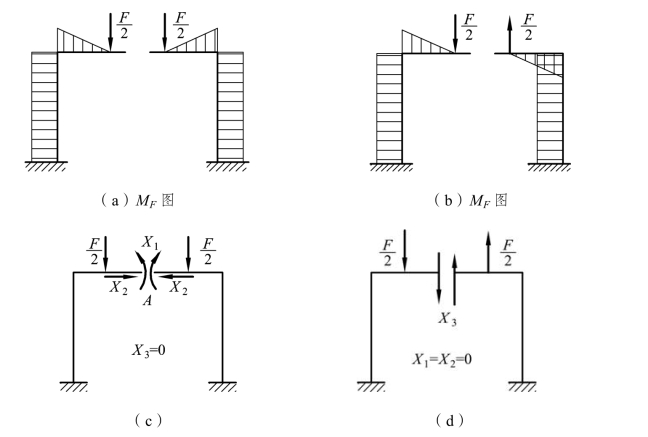
pagenumber_ebook=151,pagenumber_book=144

图6-22

（2）反对称荷载作用于对称结构。

pagenumber_ebook=151,pagenumber_book=144

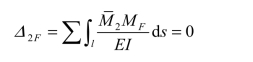
pagenumber_ebook=152,pagenumber_book=145

将上式代入力法方程中（a）式，可得对称未知力X1＝0，X2＝0。此时力法方程简化为

这时只需按（c）式计算反对称未知力 X3，如图 6-22（d）所示。

由此可得出如下结论：对称结构在对称荷载作用下，结构的内力（以及变形）是对称的，反对称的多余未知力为零；对称结构在反对称荷载作用下，结构的内力（以及变形）是反对称的，对称的多余未知力为零。利用这一性质可以简化计算，并可以用来检查内力图是否正确。

对称结构在非对称荷载作用下，可以分解成正对称荷载和反对称荷载两部分，对两部分分别进行计算，然后将两者所得内力叠加，即得原结构的最终内力。

【例题 6-7】绘制图 6-23（a）所示刚架在对称荷载作用下的M 图，EI 为常数。

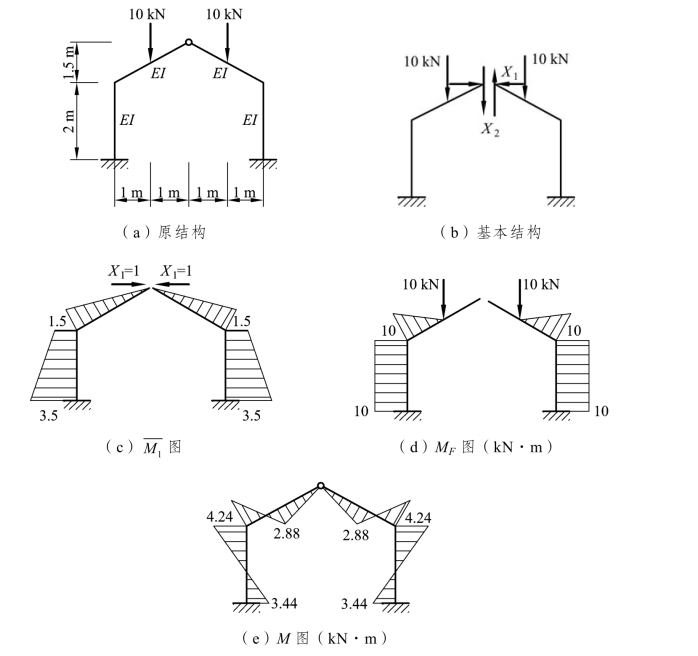
pagenumber_ebook=152,pagenumber_book=145

图6-23

解：此刚架是对称结构，且荷载也是对称的。我们将中间铰去掉，代之以两对多余未知力X1和X2，得到对称的基本结构，如图 6-23（b）所示。其中多余未知力X1是对称的，X2是一对反对称未知力，由于对称结构在对称荷载作用下，反对称的未知力为零。因此，X2＝0，只需计算对称的未知力X1，建立力法方程

绘制单位弯矩图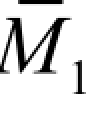 pagenumber_ebook=153,pagenumber_book=146 图和荷载弯矩图 MF图，分别如图 6-23（c）、（d）所示，求得系数和自由项为

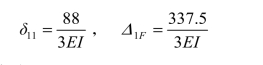
pagenumber_ebook=153,pagenumber_book=146

代入力法方程，解得

最后弯矩按式计算，据此绘出弯矩图，如图 6-23（e）所示。

【例题6-8】利用结构的对称性绘制图 6-24（a）所示刚架的弯矩图。

pagenumber_ebook=153,pagenumber_book=146

图6-24

解：这是一个三次超静定对称刚架，荷载是非对称的。将荷载分解成对称荷载和反对称荷载，如图 6-24（b）、（c）所示。在对称荷载作用下，如果忽略横梁的轴向变形，则只有横梁承受压力 F/2，其他杆件无内力。因此，为了求图 6-24（a）所示刚架的弯矩图，只需求图6-24（c）在反对称荷载作用下的弯矩图即可。

选取对称的基本结构，切开横梁对称轴处截面，由对称性质可知，截面上对称的多余未知力（轴力和弯矩）为零，只需计算反对称的未知力X1，如图 6-24（d）所示。据切口两侧截面相对位移为零的条件，建立力法方程

pagenumber_ebook=153,pagenumber_book=146

绘制荷载弯矩图MF图和单位弯矩图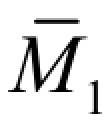 pagenumber_ebook=154,pagenumber_book=147 图，如图 6-24（e）、（f）所示，计算系数和自由项如下：

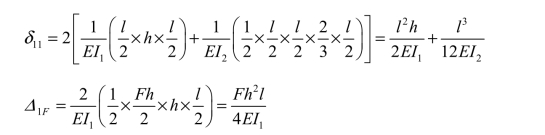
pagenumber_ebook=154,pagenumber_book=147

代入力法方程，令

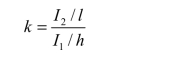
pagenumber_ebook=154,pagenumber_book=147

得

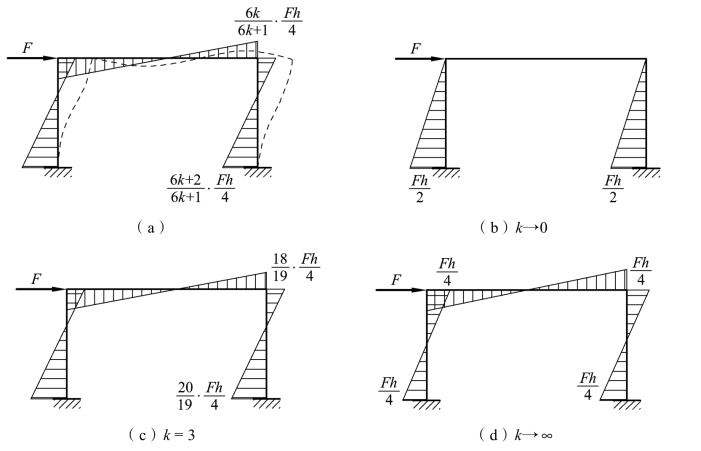
pagenumber_ebook=154,pagenumber_book=147

图6-25　M 图

现在进一步讨论刚架弯矩图随横梁与立柱相对刚度比值 k 的变化规律，当横梁的I2远小于立柱的I1时，即k →0 时，弯矩图如图 6-25（b）所示，柱中弯矩的零点在柱顶；当横梁的I2远大于立柱的I1时，即k→∞，弯矩图如图 6-25（d）所示，此时，柱的弯矩零点趋于柱中点；在一般情况下，柱的弯矩图有零点，且零点在柱的中点以上的半柱范围内变动，当k＝3 时，柱弯矩的零点位置与柱中点很接近，如图 6-25（c）所示。

选取对称基本结构的方法

相关推荐