位移法方程可写为式（7-5）即为位移法方程的一般形式，不论结构是什么形式，位移法方程的形式是不变的，故式（7-5）称为位移法典型方程。由以上的分析可知，位移法方程的实质是一组平衡方程。在位移法计算中，只需做平衡条件校核。......
2023-08-30
结构力学：快速学会力法计算步骤及算例
【摘要】：根据力法的基本原理，力法计算超静定结构的方法和步骤可归纳如下：确定超静定次数，并选取适当的基本结构。应当注意的是，在选取基本结构时，若解除多余约束的方案不同，则将会得到不同形式的基本结构，虽然其力法典型方程的基本形式相同，超静定结构的求解步骤和最终结果亦相同，但计算工作量可能会有很大的差异。以下分别举例说明用力法计算各类超静定结构的具体计算方法。
根据力法的基本原理，力法计算超静定结构的方法和步骤可归纳如下：
（1）确定超静定次数，并选取适当的基本结构。
（2）根据原结构中各个被解除约束方向的已知位移条件，建立力法典型方程式。
（3）分别作出基本结构的各单位内力图及已知外荷载所产生的内力图，并应用公式（6-3）求出所有的系数和自由项。
（4）将求得的系数和自由项代入力法典型方程式，并解出各基本未知力。
（5）按分析静定结构的方法，利用静力平衡条件或叠加原理（按公式6-4）作出结构的最后内力图。梁、刚架：
，再由平衡条件求得其轴力和剪力；桁架：
。
（6）校核（后面详述）。
应当注意的是，在选取基本结构时，若解除多余约束的方案不同，则将会得到不同形式的基本结构，虽然其力法典型方程的基本形式相同，超静定结构的求解步骤和最终结果亦相同，但计算工作量可能会有很大的差异。因此，基本结构的合理选取在力法中常具有重要意义。合理选取基本结构总的原则是使计算简单。例如，对于梁和刚架结构来说，应该使单位荷载弯矩图和荷载弯矩图的图形比较简单，甚至仅发生于局部，以便于图乘法的运用，或是使方程的某些副系数或自由项等于零：若是对称结构，一般宜取对称的基本结构；对于有弹性支座的情况，去除多余约束时通常可将弹性支座切断，运算较为简单。
以下分别举例说明用力法计算各类超静定结构的具体计算方法。
【例题6-1】 试计算图 6-11 所示连续梁，并绘制其最终弯矩图，各跨EI 为常数。
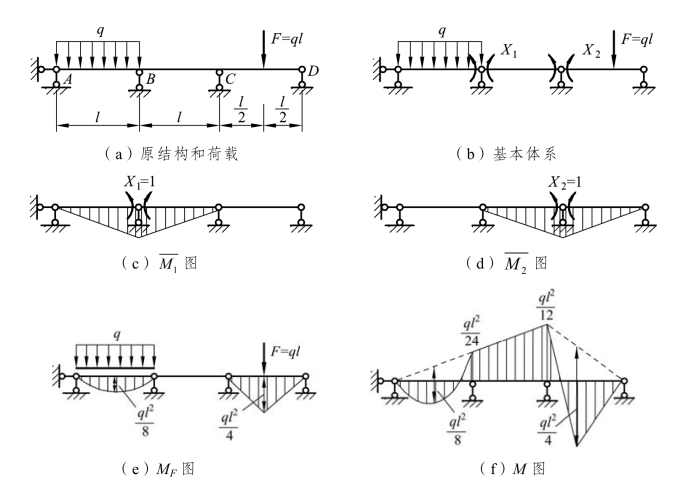
图6-11
解：（1）确定超静定次数，选取基本体系。
此梁是两次超静定结构，在基本体系的诸多方案中，以图 6-11（b）所示简支梁式基本体系最便于计算，即去除支点 B、C 两截面的相对转动约束而成铰结点，X1和X2分别表示截面 B 和 C 的未知弯矩。
（2）根据原结构已知变形条件建立力法典型方程。
原连续梁受力变形后是连续的，结点 B 和 C 的左、右截面不会产生相对转角，故力法典型方程为：
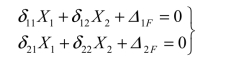
（3）求系数和自由项。
绘出基本结构在单位力X1＝1、X2＝1 作用下的弯矩图
及荷载作用下的弯矩图MF，如图 6-11（c）、（d）、（e）所示。运用图乘法求得
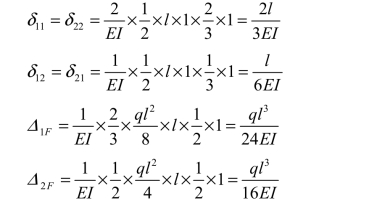
由以上计算可见，取简支梁为基本结构可使
图及MF的分布范围仅限于局部，位移计算就会比较简单，如果连续梁跨数更多时，这一优点更为明显，并将使不相邻的未知力之间的副系都等于零。
（4）代入方程求出基本未知量。
将以上所得各位移值代入力法典型方程，即有
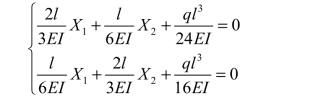
解得：
负号表示 X1、X2的方向与所设方向相反，截面 B、C 均为上边缘受拉。
（5）绘制最终弯矩图。
用叠加法绘出弯矩图，如图 6-11（f）所示。根据梁上的荷载和已求得的杆端弯矩，用平衡条件可作出梁段的剪力图并求出各支座反力。
【例题 6-2】 试计算图 6-12（a）所示的超静定刚架，并绘制内力图。
图6-12
解：（1）确定超静定次数，选取基本结构。
这是一个二次超静定结构，去掉B 端铰支座的两个约束，得到基本结构，如图 6-12（b）所示。
（2）建立力法方程。基本结构在荷载和多余未知力作用下，应满足B 点的水平和竖向位移为零的变形条件，建立力法方程：
（3）计算系数和自由项。先分别绘制基本结构在荷载作用下的MF图［见图 6-12（e）］及单位力 X1＝1，X2＝1 作用下的
图和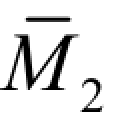
图［见图 6-12（c）、（d）］，利用图乘法计算各系数和自由项如下，有
（4）求多余未知力。将上述各系数和自由项代入力法方程，并求解得
负号表示 X2的方向与所设方向相反。
（5）绘制内力图。利用叠加公式
，计算各杆端的弯矩值如下：
绘制弯矩图，如图 6-13（a）所示。
剪力和轴力可按分析静定结构的方法，利用平衡条件计算，并绘制剪力图和轴力图，分别如图 6-13（b）、（c）所示。
图6-13
【例题 6-3】 作图 6-14（a）所示超静定梁的弯矩图。
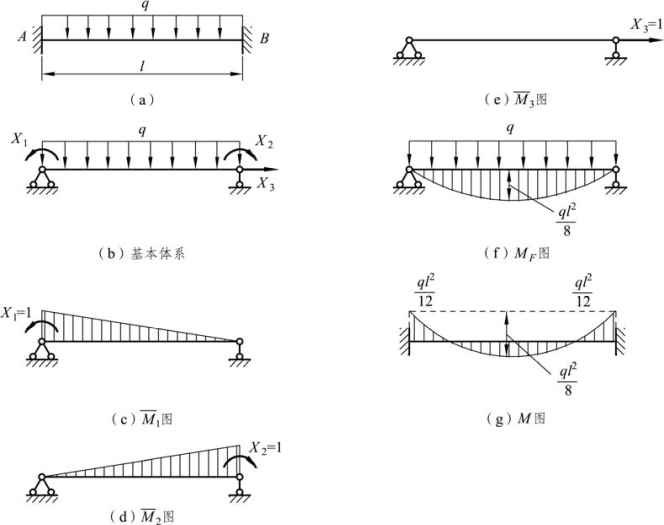
图6-14
解：（1）取基本体系，如图 6-14（b）所示。其中 X1、X2分别为 A、B 端的弯矩；X3为B 端的轴向力。
（2）建立力法典型方程。
根据原结构的已知位移条件，力法典型方程为
据此可得X3=0，即小挠度情况下的超静定梁在垂直于梁轴的横向荷载作用下，其轴向力等于零，因此力法典型方程简化为：
（3）求系数和自由项。
应用图乘法，可得
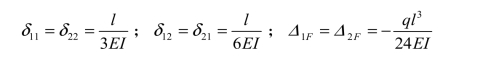
（4）求多余未知力并作 M 图。
将系数和自由项代入力法典型方程，可得
由此作出最后的弯矩如图 6-14（g）所示。此种两端固定的直梁可按二次超静定处理。
【例题6-4】 试计算图 6-15（a）所示超静定桁架各杆件的内力。已知各杆的 EA 相同。
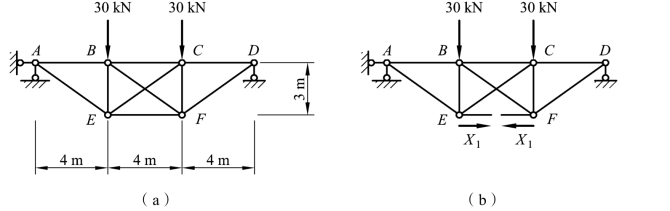
图6-15
解：（1）选取基本结构。此结构为一次超静定桁架，切断下弦杆EF 代之以相应的多余未知力 X1，得到图 6-15（b）所示静定桁架作为基本结构。
（2）建立力法方程。按照原结构变形连续的条件，基本结构上与 X1相应的位移，即切口两侧截面沿杆轴方向的相对位移应为零，故力法方程为
（3）计算系数和自由项。基本结构分别受单位力 X1＝1 和荷载作用引起的各杆内力列入表 6-1 中， δ11、 Δ1F的计算也已在该表中列出。由表可得
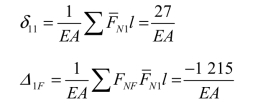
表6-1 δ11、Δ1F及 FN的计算
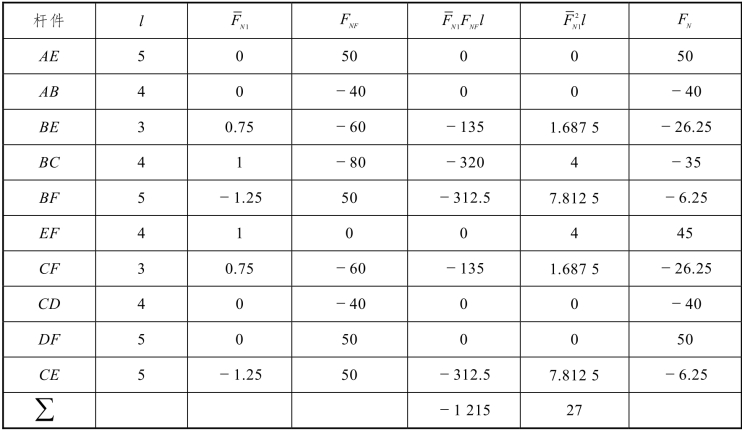
（4）求多余未知力：将以上系数和自由项代入力法方程，得
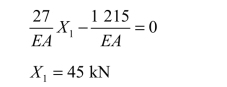
（5）计算各杆内力：根据叠加原理，各杆内力为
由此式计算得到各杆轴力，结果列入表的最后一栏。
【例题6-5】 计算图 6-16（a）所示两跨排架，作出弯矩图。其中：EI2＝5EI1，h1＝3 m，h2＝10 m，ME＝20 kN·m，MH＝60 kN·m，杆 CD、杆HG 的 EA＝∞。
解：排架的计算方法与前面讲的刚架基本相同，特别之处是：理论上它的基本体系也有多种取法，但是根据经验切断EA＝∞的横杆，代之以多余力而得到基本体系是最方便的，如图 6-16（b）所示。这是因为这种基本体系中的柱子全是悬臂结构，后面计算系数和自由项时比较方便。
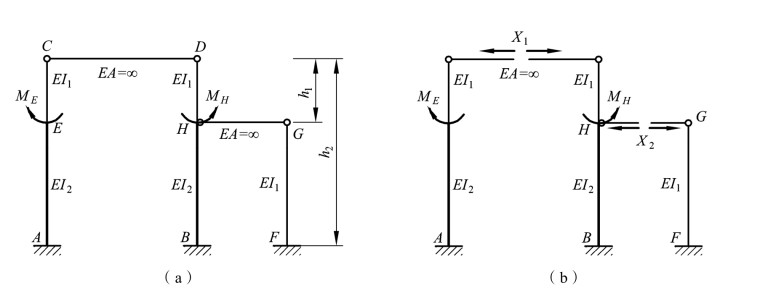
图6-16
由于基本体系是把轴力杆切断而得到的，因此建立力法方程的位移条件是：基本体系在荷载及多余力共同作用下，在切断点处产生的沿多余力方向的相对水平位移应该等于零，因为结构上的任意一点在荷载作用下可能会产生变形和位移，但不可能有相对位移，所谓的相对位移是多点之间的。下面来说明它的计算方法及步骤。
（1）此排架为二次超静定结构，选取基本体系，如图 6-16（b）所示。
（2）建立力法方程。
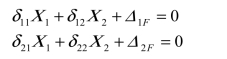
（3）作M1、M2、MF图，如图 6-17（a）、（b）、（c）所示，求系数及自由项。
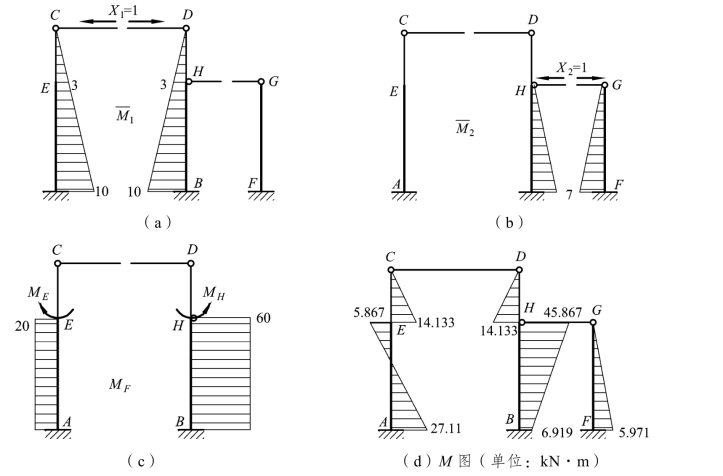
图6-17
注意：作M1图时，一对多余力Xl＝1 是作用在切断杆上的，因此该杆受轴力为－1，但计算δ11时，由于该杆的EA＝∞，因此没有影响。由图乘法得系数及自由项如下：
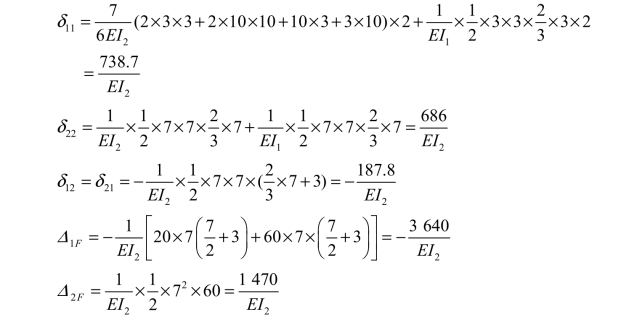
（4）解力法方程，求多余未知力。
将求得的系数和自由项代入力法方程中。
解得：
（5）作最后弯矩图。
根据叠加法M =M1X1+M2X2+MF，求得杆端弯矩，绘制出弯矩图，如图 6-17（d）所示。
【例题6-6】 试计算图6-18 所示加劲梁，已知梁的抗弯刚度为 E1I，各链杆的抗拉压刚度为 E2A。
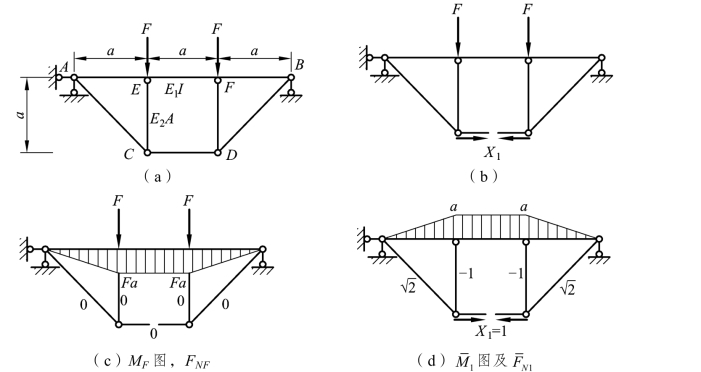
图6-18
解：这是一次超静定的组合结构。切断链杆 CD 便得基本结构，如图 6-18（b）所示，根据切口两侧截面沿X1方向的相对位移为零的条件，可列出典型方程：
在组合结构中，计算系数和自由项时，对于梁仍只考虑弯矩的影响；对于链杆则只需考虑轴力。作基本结构在荷载单独作用下的弯矩图MF和各链杆的轴力 FN图（标注在杆旁），如图 6-18（c）所示。作基本结构在X1=1单独作用下的弯矩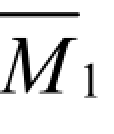
图和各链杆的轴力
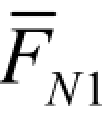图，如图 6-18（d）所示。据此，可算得系数和自由项如下：
带入力法典型方程并求解：
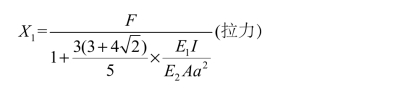
梁的最后弯矩图和各链杆的轴力，可按下面二式叠加而得：
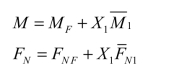
由图 6-18（c）、（d）可知，
与MF的符号是相反的，故按上式叠加的结果，梁中的弯矩 M ＜MF，又由图 6-18（c）可知，MF图实质上是没有链杆的简支梁的弯矩图，这就表明原结构（加劲梁）由于有链杆的支撑，梁中的弯矩（M）比相应的简支梁明显地减小了。或者说，链杆的存在，使梁的强度和刚度得到了增加。这就是“加劲梁”名称的由来，起重运输机械中的天车梁就常采用这种结构。
通过以上几个例题的计算表明，超静定结构在荷载作用下的内力与各杆刚度的绝对值无关，但与各杆刚度的相对比值有关。相对刚度愈大，承受的内力也愈大。这是超静定结构受力的重要特征之一。
有关结构力学的文章
- 详细阅读
-
算例介绍及仿真分析详细阅读
图7-8 风向γ=3°时风电场等效模型3.风电场故障电流特征仿真t=4s时刻，在主变压器低压侧F1点发生三相金属性短路，故障持续时间为0.1s，故障后5ms风电机组投入Crowbar电路，故障前STH风电场输入风速为10m/s。动作电流与制动电流均不再恒定并叠加有其他频率分量，会发生大范围抖动。......
2023-06-28
- 详细阅读
-
问卷法的应用及影响-以社交媒体公信力为例详细阅读
问卷法也是常采用的研究方法之一，随着互联网的发展，网络问卷成了研究者青睐的研究方法。网络问卷的公告一般被放置在博客、邮件列表以及社交网站中，采用多级评价制来获取受访者的看法。[84]Deborah S.Chung &Seungahn Nah调查公民记者对自身的角色概念认知时，也使用了问卷法。......
2023-11-21
-
UGNX8.0快速入门教程：创建解算方案步骤详细阅读
创建解算方案就是创建一个新的解算方案，可以定义分析类型、解算方案类型及特定于解算方案的载荷和运动驱动。图9.3.1所示的“解算方案”对话框的说明如下。图9.3.1“解算方案”对话框●：该下拉列表用于选取解算方案的分析类型。......
2023-11-23
-
经典算例展示与分享详细阅读
图9.9弹靶侵彻过程提取弹丸的速度-时间曲线，如图9.10所示。采用cm-g-μs单位制。有限元模型如图9.12所示。表9.1常见炸药的JWL参数所需拼接盖板长度L=l+13mm=mm=580.12mm，取580mm。......
2023-06-22
-
结构力学,力法基本原理解析详细阅读
如图 6-8所示，X1表示被去掉的多余约束的反力，暂时是未知的，故称为多余约束未知力或力法的基本未知量。由于 δ11和 Δ1F是静定结构在已知力作用下的位移，均可按前章所述计算位移的方法求得，因此，解上述方程，可求得多余未知力X1。......
2023-08-30
-
算例介绍与仿真分析详解详细阅读
4.风电场对方向保护影响仿真根据对风电机组暂态电压、电流特性的分析结果，经过不同类型故障仿真计算，传统提取工频分量的傅里叶滤波算法得到的相位结果误差很大，对基于电压、电流相位关系方向元件的动作特性影响十分严重[4]。......
2023-06-28
相关推荐