根据叠加原理，式可写成以下形式：图14-12位移条件式就是为求解多余未知力X1和X2所需要建立的力法方程。对于高次超静定问题，其力法方程也可类似推出。当原结构在去掉多余约束处的已知位移为零时，其力法方程为方程中的系数称为柔度系数，位于主对角线上的系数δii称为主系数，在主对角线两侧的系数δij称为副系数，Δ1P称为自由项。由于基本体系是静定的，所以力法方程中各系数和自由项都可以按照上一单元位移计算的方法求出。......
2023-06-16
结构力学：力法典型方程实例
【摘要】：下面结合三次超静定的刚架来进一步说明用力法解多次超静定结构的一般原理和力法典型方程的建立。上述方程组在组成上具有一定的规律性，不论超静定结构的类型、超静定次数以及所选的基本结构如何，所得的方程都具有式（6-2）的形式，故称之为力法的典型方程。力法方程最后一项位移 ΔiF称为自由项。
上面我们根据一次超静定结构的计算说明了力法的基本原理，力法计算超静定结构的关键在于根据位移条件建立力法的基本方程，以求解多余未知力。对于多次超静定结构，其计算原理与一次超静定结构完全相同。下面结合三次超静定的刚架来进一步说明用力法解多次超静定结构的一般原理和力法典型方程的建立。
图 6-9（a）所示的刚架为三次超静定结构，用力法求解时，去掉B 处的三个多余约束，代之以相应的多余未知力X1、X2、X3，则得到图 6-9（b）所示的基本结构。在原结构中，由于B 端为固定端，所以没有水平位移、竖向位移和转角位移。因此，基本结构在荷载和多余未知力 X1、X2和 X3共同作用下，在B 端产生的X1、X2和X3方向上的位移Δ1、Δ2、Δ3都应等于零。即：
由叠加原理，在基本结构上可分别求出位移Δ1、Δ2、Δ3。设基本结构在单位力X1＝1 单独作用下，B 点沿X1、X2和 X3方向所产生的位移分别为δ11、δ21和δ31［见图 6-9（c）］，事实上，X1并不等于 1，因此将图 6-9（c）各方向的位移分别乘以 X1，即得X1作用时B 点的水平位移δ11X1、竖向位移δ21X1和转角位移δ31X1。同理，由图6-9（d）得X2单独作用于基本结构时B 点的水平位移δ12X2、竖向位移δ22X2和转角位移δ32X2。由图 6-9（e）得 X3单独作用于基本结构时 B 点的水平位移 δ13X3、竖向位移 δ23X3和转角位移δ33X3。在图 6-9（f）中，Δ1F、Δ2F、Δ3F分别表示当荷载单独作用于基本结构上B 点的水平位移、竖向位移和转角位移。
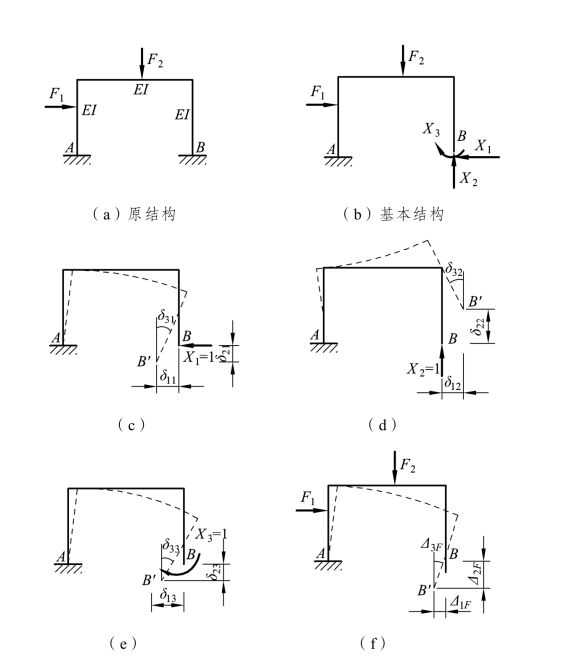
图6-9
根据叠加原理，基本结构在多余未知力X1、X2、X3及荷载F 共同作用下产生的位移，等于它们分别作用时所产生的位移总和。即基本结构应满足的位移条件表示为：
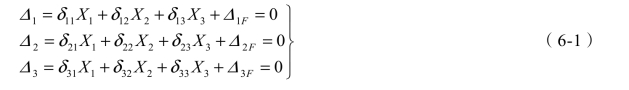
式（6-1）通常称为力法典型方程，方程中每一式的物理意义是：基本结构中在各多余未知力和已知荷载共同作用下，每一个多余未知力方向上的位移应与原结构中相应的位移相等。
对于图 6-9 所示的刚架，力法基本结构的选取方案并不是唯一的，在图 6-10 中给出了其他形式的基本结构，这时力法方程在形式上与式（6-1）完全相同。但由于 X1、X2和 X3的实际含义不同，因而变形协调条件的含义也不同。此外，还须注意，基本结构必须是几何不变的，瞬变体系不能用作基本结构。
对于 n 次超静定结构，用力法分析时，可去掉n 个多余约束得到静定的基本结构，具有n 个多余未知力X1，X2，…，Xn，相应地具有 n 个位移条件，可建立 n 个方程，若 n 个多余约束方向的位移均已知为零（仅有荷载作用的情况），则力法典型方程可表达为：
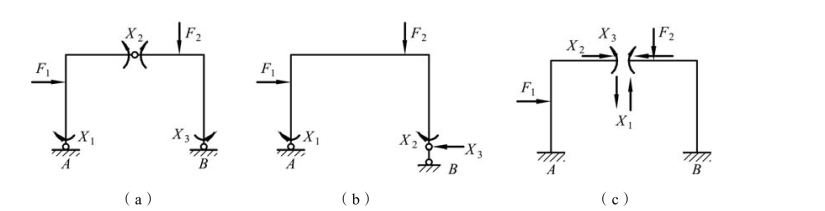
图6-10
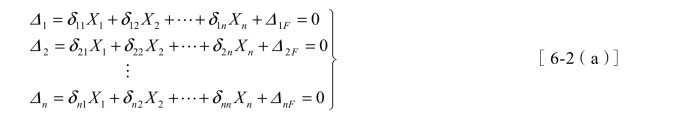
或简记为：
也可用矩阵表示为：
上式中由δij柔度系数组成的矩阵称为柔度矩阵，它是一个对称矩阵，因此，力法方程也称为柔度方程，力法也称为柔度法。
上述方程组在组成上具有一定的规律性，不论超静定结构的类型、超静定次数以及所选的基本结构如何，所得的方程都具有式（6-2）的形式，故称之为力法的典型方程。
在此方程组中，主斜线上未知力的系数 δii称为主系数，也称为主位移，其方向总是与单位未知力Xi＝1 所设方向一致，所以总是正的，且不等于零。在主斜线两侧的未知力前的系数 δij称为副系数，由位移互等定理可知δij＝δji。力法方程最后一项位移 ΔiF称为自由项。副系数及自由项的具体数值可能为正号，或负号，或为零。
上述所有系数和自由项均可用位移计算公式求得。若超静定结构含有受弯杆件及仅受轴力的链杆，而忽略受弯杆件的剪切变形和轴向变形，则有
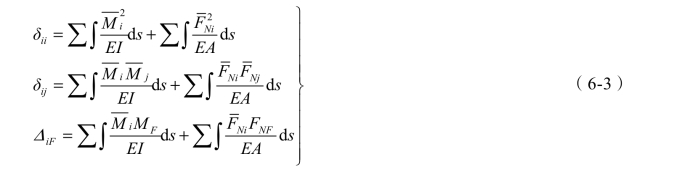
式中，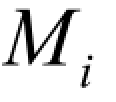
、
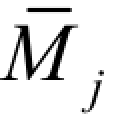、MF和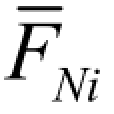
、
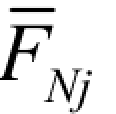、 FNF分别代表Xi= 1、Xj= 1及荷载单独作用于基本结构时产生的弯矩和轴力。
将求得的各系数和自由项代入力法方程（6-2），求解联立线性方程组，即可求得多余约束力X1，X2，…，Xn。基本结构在相应的多余约束力及荷载共同作用下，运用平衡条件可求出所有截面的内力，它就是原超静定结构的全部解答。另外，也可利用叠加原理，利用计算过程中已得的基本结构受各力单独作用下的内力分布（Mi、MF等），求出原超静定结构任一截面的内力，例如任一截面的最终弯矩值为：
再根据平衡条件可求得剪力和轴力。
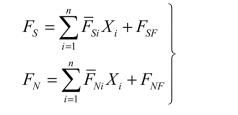
有关结构力学的文章
- 详细阅读
-
结构力学中的7.4位移法典型方程及算例详细阅读
位移法方程可写为式（7-5）即为位移法方程的一般形式，不论结构是什么形式，位移法方程的形式是不变的，故式（7-5）称为位移法典型方程。由以上的分析可知，位移法方程的实质是一组平衡方程。在位移法计算中，只需做平衡条件校核。......
2023-08-30
-
结构力学,力法基本原理解析详细阅读
如图 6-8所示，X1表示被去掉的多余约束的反力，暂时是未知的，故称为多余约束未知力或力法的基本未知量。由于 δ11和 Δ1F是静定结构在已知力作用下的位移，均可按前章所述计算位移的方法求得，因此，解上述方程，可求得多余未知力X1。......
2023-08-30
-
虚功原理和单位力法解析-结构力学详细阅读
变形体系的虚功原理可表述为：变形体系处于平衡的必要和充分条件是，对于符合变形体系约束条件的任意微小的连续虚位移，变形体系上所有外力所做的虚功总和外W ，等于变形体系各微段截面上的内力在其虚变形上所做的虚功总和U变。虚功原理更一般地表示为：由以上可见，虚功原理需要涉及两个状态，取一个状态的外力和内力，取另一个状态的位移和变形。如果位移是虚设的，则称为虚位移原理；如果外力是虚设的，则称为虚力原理。......
2023-08-30
-
结构力学：快速学会力法计算步骤及算例详细阅读
根据力法的基本原理，力法计算超静定结构的方法和步骤可归纳如下：确定超静定次数，并选取适当的基本结构。应当注意的是，在选取基本结构时，若解除多余约束的方案不同，则将会得到不同形式的基本结构，虽然其力法典型方程的基本形式相同，超静定结构的求解步骤和最终结果亦相同，但计算工作量可能会有很大的差异。以下分别举例说明用力法计算各类超静定结构的具体计算方法。......
2023-08-30
-
结构力学：位移法概念简介详细阅读
位移法是以结构的结点位移作为基本未知量，取超静定的单个杆件及其组成的体系作为基本结构，通过平衡条件建立位移法方程，求出位移后，即可利用位移和内力之间的关系，求出杆件和结构的内力。通过下面简单例子具体说明位移法的基本原理和计算方法。综上所述，位移法的基本思路是“先固定后复原”。......
2023-08-30
-
典型传动装置装配实例分享详细阅读
为了保证正常的啮合传动，齿轮与齿条间应有一定的啮合间隙，因此，在装配溜板箱与齿条时就应保证这一要求。在上述两装配尺寸链中，由于组成环较多，封闭环的公差又比较小，所以总装时进给箱、溜板箱和后支架的装配不应采用完全互换法。偏移量的大小取决于各组成环的累积误差，但装配时实际允许的偏移量，则取决于螺钉过孔和螺钉间的径向间隙。......
2023-06-29
-
应用截面法计算轴力及绘制轴力图的实例分析详细阅读
4-1 试用截面法计算图4-34 所示杆件各段的轴力，并作轴力图。4-3 圆截面钢杆长l=3 m，直径d=15 mm，两端受到F=100 kN 的轴向拉力作用时伸长Δl=2.5 mm。4-4 阶梯状直杆受力如图4-35 所示。图4-35题4-4图4-5 如图4-36 所示阶梯形圆截面杆，承受轴向载荷F1=50 kN 与F2 作用，AB 与BC 段的直径分别为d1=20 mm 和d2=30 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求载荷F2 之值。4-6 如图4-37 所示桁架，杆1 与杆2 的横截面均为圆形，直径分别为d1=30 mm 与d2=20 mm，两杆材料相同，许用应力[σ]=160 MPa。......
2023-06-19
相关推荐