变形体系的虚功原理可表述为：变形体系处于平衡的必要和充分条件是，对于符合变形体系约束条件的任意微小的连续虚位移，变形体系上所有外力所做的虚功总和外W ，等于变形体系各微段截面上的内力在其虚变形上所做的虚功总和U变。虚功原理更一般地表示为：由以上可见，虚功原理需要涉及两个状态，取一个状态的外力和内力，取另一个状态的位移和变形。如果位移是虚设的，则称为虚位移原理；如果外力是虚设的，则称为虚力原理。......
2023-08-30
结构力学,力法基本原理解析
【摘要】：如图 6-8所示，X1表示被去掉的多余约束的反力，暂时是未知的，故称为多余约束未知力或力法的基本未知量。由于 δ11和 Δ1F是静定结构在已知力作用下的位移，均可按前章所述计算位移的方法求得，因此，解上述方程，可求得多余未知力X1。
超静定结构与静定结构的根本区别在于有多余约束，从而有多余未知力，如果能设法求出多余未知力，则超静定结构的计算就可转化为在多余未知力及荷载共同作用下的静定结构的计算问题了，所以用力法计算的关键在于求解多余未知力。
如图 6-8（a）所示为一次超静定梁，为了使它变为静定的基本结构，可将支座B 的支杆作为多余约束去掉，并代之以多余未知力X1，作为外荷载作用在结构上。如图 6-8（b）所示，X1表示被去掉的多余约束的反力，暂时是未知的，故称为多余约束未知力或力法的基本未知量。经过这样处理之后，从结构形式上看，虽已有所变化，由超静定结构变为静定结构，但从实质上看，结构的实际受力情况却完全没有改变，因而结构的内力及其变形，也同原来的超静定结构完全一样。因此，如果能把后者的内力求出来，那么，也就等于获得了前者的内力。
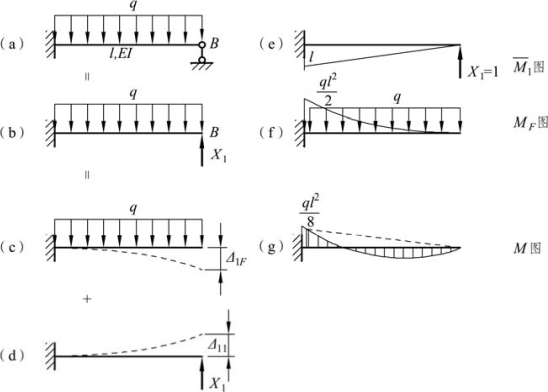
图6-8
图 6-8（b）所示的体系既然是一个静定结构，那就可以应用前面所学到的知识计算其内力和位移。为了计算方便，根据线性变形体系其内力和位移可叠加的特性，将基本结构上的荷载分为两个部分：第一部分为结构上原有的已知荷载，第二部分为基本未知力X1，并将它们分别作用在基本结构上，如图 6-8（c）、（d）所示。其中，每个图中的虚线分别表示由该部分的外力所产生的变形或位移。
在图 6-8（c）中，Δ1F为在 X1的方向由已知外荷载所产生的位移。在图 6-8（d）中，Δ11为 X1的方向由其本身所产生的位移，其中Δ11=δ11X1， δ11为X1=1时产生的位移，如图6-8（e）所示。
因此，若将图 6-8（c）、（d）所示的两种情况相叠加，则可得X1方向的总位移为：
显然，上述两种情况相叠加，实际上就是图 6-8（b）所示的情况，而图 6-8（b）所示的情况，应与原结构图 6-8（a）所示的情况是相同的，因为原结构B 点是一个活动铰支座，沿X1方向都没有发生位移，故可知 Δ1= 0，所以由上式可得：
上式是根据超静定结构的实际变形条件建立的，故称为变形协调方程或力法方程。
由于 δ11和 Δ1F是静定结构在已知力作用下的位移，均可按前章所述计算位移的方法求得，因此，解上述方程，可求得多余未知力X1。
为了计算 δ11和Δ1F，可分别绘出基本结构在单位力X1= 1单独作用下的单位弯矩图M1图［见图 6-8（e）］和荷载单独作用下的弯矩图MF［见图6-8（f）］，然后，应用图乘法，可得
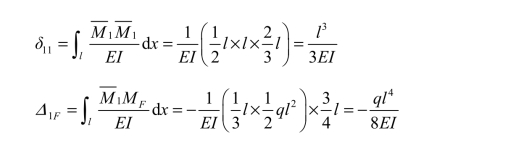
代入上述力法方程式，则有
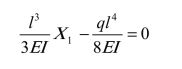
解得
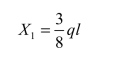
所得未知力X1为正号，表示反力X1实际方向与所设的方向相同。
多余未知力X1求出后，其余所有反力和内力都可用静力平衡条件确定，在绘制最后弯矩M 图时，可利用已经绘出的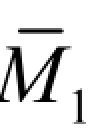
和MF图，根据叠加原理绘制，即M=
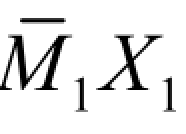+MF，如图6-8（g）所示为最后的弯矩图。
有关结构力学的文章
- 详细阅读
-
结构力学：快速学会力法计算步骤及算例详细阅读
根据力法的基本原理，力法计算超静定结构的方法和步骤可归纳如下：确定超静定次数，并选取适当的基本结构。应当注意的是，在选取基本结构时，若解除多余约束的方案不同，则将会得到不同形式的基本结构，虽然其力法典型方程的基本形式相同，超静定结构的求解步骤和最终结果亦相同，但计算工作量可能会有很大的差异。以下分别举例说明用力法计算各类超静定结构的具体计算方法。......
2023-08-30
-
力法基本原理-建筑力学（第3版）详细阅读
力法是计算超静定结构最基本的方法，下面先用一个例子说明力法的基本原理。这个静定梁称为原超静定梁的基本结构。若用Δ1q和Δ11分别表示荷载q和多余未知力X1单独作用下基本结构在X1作用处沿X1方向产生的位移，则由叠加原理根据位移条件可得下列方程：若X1＝1，在X1方向产生的位移为δ11，则有Δ11＝δ11X1，于是式可以写成这就是求解多余未知力的补充方程，称为力法方程。......
2023-08-26
-
结构力学：力法典型方程实例详细阅读
下面结合三次超静定的刚架来进一步说明用力法解多次超静定结构的一般原理和力法典型方程的建立。上述方程组在组成上具有一定的规律性，不论超静定结构的类型、超静定次数以及所选的基本结构如何，所得的方程都具有式（6-2）的形式，故称之为力法的典型方程。力法方程最后一项位移 ΔiF称为自由项。......
2023-08-30
-
结构力学：位移法概念简介详细阅读
位移法是以结构的结点位移作为基本未知量，取超静定的单个杆件及其组成的体系作为基本结构，通过平衡条件建立位移法方程，求出位移后，即可利用位移和内力之间的关系，求出杆件和结构的内力。通过下面简单例子具体说明位移法的基本原理和计算方法。综上所述，位移法的基本思路是“先固定后复原”。......
2023-08-30
- 详细阅读
-
牛顿拉夫逊法的基本原理及应用详细阅读
迭代过程一直进行到满足收敛判据为止，其中ε1、ε2为预先给定的小正数。牛顿—拉夫逊法的思想是微分学，它将求解非线性方程的问题转化成反复求解一组线性化的修正方程，并对变量进行修正的迭代过程。它同样存在初值选取问题，当初值选取离真解较远时，就失去牛顿—拉夫逊法的成立基础，将对收敛产生影响。......
2023-06-15
-
涂层设计的基本原理解析详细阅读
2）合理进行涂层设计，包括正确选择喷涂材料、设备、工艺及遵循严格的涂层质量评价体系对涂层性能进行检验等。涂层设计起着承上启下的作用，是采用热喷涂技术成功解决实际问题的基础，是最重要的环节之一，在进行涂层设计时要考虑涂层所涉及的各个环节，具有明显的系统特性。......
2023-06-18
相关推荐