静定结构在支座移动时，只发生刚体位移，不产生内力和变形。这种位移可通过几何关系求得，也可应用单位力法进行计算。在式中，乘积的正负号规定为：当虚拟状态的支座反力与实际支座位移的方向一致时取正号，相反时取负号。 刚架的支座位移如图 5-19所示，试求 A 点的水平位移 ΔAx和 C 点左右截面的相对转角位移 θCC。......
2023-08-30
结构力学：温度作用下的位移计算
【摘要】：在使用时，这些结构所处的环境温度相对于建造时的温度一般要发生变化，这种温度的改变将会引起构件的变形，从而使结构产生位移。对于静定结构，温度改变只会引起材料的自由膨胀、收缩，在结构中不会引起内力，但将产生变形和位移。静定结构由于温度改变引起的位移计算公式，仍可由位移计算的一般公式导出。因此，点 C 的竖向位移为计算结果为负，表示 ΔCy的方向与所设单位力的方向相反，即 ΔCy向上。
工程结构都是在某一温度范围内建造的。在使用时，这些结构所处的环境温度相对于建造时的温度一般要发生变化，这种温度的改变将会引起构件的变形，从而使结构产生位移。
对于静定结构，温度改变只会引起材料的自由膨胀、收缩，在结构中不会引起内力，但将产生变形和位移。
静定结构由于温度改变引起的位移计算公式，仍可由位移计算的一般公式（5-17）导出。但应注意，式（5-17）中微段的变形是由材料的自由膨胀、收缩引起的。
如图 5-20（a）所示刚架，设外侧温度升高t1，内侧温度升高t2，且t2＞t1，并假定温度沿截面的高度h 为线性分布，则在发生变形后，截面还将保持为平面。从杆件中取出一微段ds［见图 5-20（b）］，杆件轴线处的温度为
如果杆件截面对称于形心轴（h1＝h2＝h/2），则有
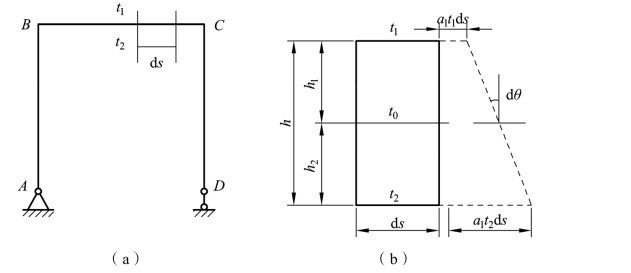
图5-20
设材料的线膨胀系数为 α，在温度改变时，该微段中性轴上纵向纤维的伸长量，即微段的轴向变形为
该微段上侧纵向纤维的伸长量为αt1d s，下侧纵向纤维的伸长量为αt2d s，由于杆内温度假定为沿截面高度按直线变化，故杆件变形时截面仍保持平面。因此，该微段两端截面的相对转角，即微段的弯曲变形为
静定结构在温度变化时，由于杆件可以自由地发生变形，故微段两端的截面不发生相对剪切位移，即
将式（c）、式（d）和式（e）代入结构位移的一般计算公式（5-17），得
在通常情况下，材料的线膨胀系数 α 及杆件上、下侧的温度沿杆件长度是不变的，可将其从积分号内移出，即
对于等截面杆件来说，截面高度h 沿杆长也不变，故亦可将其从积分号内移出，因而式（f）可写为
在应用以上两式时，正负号可按如下方法确定：比较虚拟状态的变形与实际状态由于温度改变引起的变形，若二者的变形方向相同，则取正号；反之取负号。式中的 t0和 Δt 均取绝对值进行计算。
【例题5-10】 求图 5-21（a）所示刚架上点 C 的竖向位移 ΔCy。已知刚架内侧的温度升高 10 °C，各杆截面相同且截面关于形心轴对称，材料的线膨胀系数为 α。
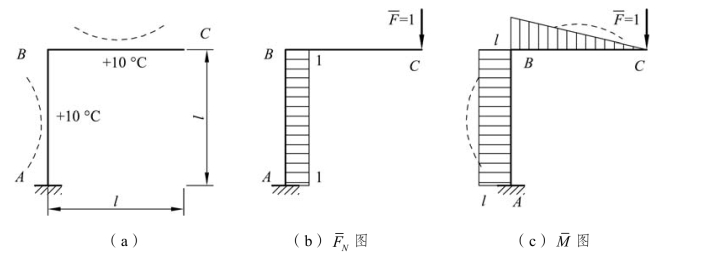
图5-21
解：在点 C 虚加一竖向单位力F = 1，绘出各杆的FN图和M 图，分别如图 5-21（b）、（c）所示。图中的虚线表示杆件的弯曲方向。可以看出，各杆的实际弯曲方向都与虚拟的相反，故在利用式（5-25）计算时，最后一项应取负值。至于轴向变形的影响一项，因杆 AB 的虚拟轴力是压力，而温度变形使其伸长，故也应取负值。因此，点 C 的竖向位移为
计算结果为负，表示 ΔCy的方向与所设单位力的方向相反，即 ΔCy向上。
有关结构力学的文章
- 详细阅读
-
温度变化下位移计算结果详细阅读
下面所说的温度均指温度的改变量，而非结构的实际温度。计算温度改变引起的位移时，仍利用变形体虚功方程。弯矩和温度改变所引起的变形方向一致时取正号；反之取负号。求温度引起的位移时，除要画 图外，还要画图。......
2023-08-26
-
结构力学：组合结构与拱位移计算详细阅读
计算结果为正，表示ΔCx的方向与所设单位力的方向相同，即 ΔCx方向向右。 求图 5-17所示半圆弧三铰拱顶铰 C 两旁截面的相对转角。图5-17解：计算拱的位移，仅考虑弯矩对弯曲变形的影响，按公式计算。计算三铰拱受荷载及单位力偶作用时［见图 5-17、］的弯矩方程，应先求出支座反力，然后列出弯矩方程。此题由于三铰拱为对称结构，可只对拱的一半列出方程。......
2023-08-30
-
结构力学：位移法概念简介详细阅读
位移法是以结构的结点位移作为基本未知量，取超静定的单个杆件及其组成的体系作为基本结构，通过平衡条件建立位移法方程，求出位移后，即可利用位移和内力之间的关系，求出杆件和结构的内力。通过下面简单例子具体说明位移法的基本原理和计算方法。综上所述，位移法的基本思路是“先固定后复原”。......
2023-08-30
-
荷载下的静定结构位移计算（建筑力学）详细阅读
图14-10利用单位荷载法计算结构位移的步骤如下：根据欲求位移选定相应的虚拟状态。列出结构各杆段在虚拟状态下和实际荷载作用下的内力方程。试计算图14-11所示的等截面简支梁中点C的竖向位移ΔCV。由于桁架及荷载对称，故只需计算一半桁架的内力。将各杆的内力代入位移计算公式得：计算结果为正值，表明C点的位移方向与虚设单位力PK的方向相同。......
2023-08-26
-
建筑力学（第3版）中荷载作用下位移计算的通用详细阅读
利用虚功原理推导结构在荷载作用下位移计算的一般公式，首先要确定力状态和位移状态。利用式计算结构位移时，应根据结构的具体情况，只考虑其中一项或两项。这种用虚设单位荷载产生的内力，在实际状态荷载所引起的位移上做虚功，而利用虚功原理计算结构位移的方法，称为单位荷载法。单位荷载法计算位移公式适用于弹性材料和非弹性材料，可以用于计算静定结构的位移，也可以用于计算超静定结构的位移。......
2023-08-26
-
结构力学：线位移法数目确定详细阅读
在确定结点线位移的数目时，由于不计受弯直杆的轴向变形，并且假设弯曲变形是微小的，即认为直杆在受弯前后其投影长度保持不变。由于在确定结点线位移数目时，不计及杆件的轴向变形和弯曲变形，因此，可以先把所有的刚性结点和固定支座全部改成铰接，使结构变成一个铰接体系。结构基本未知量的总数等于结点的角位移数和线位移数之和。......
2023-08-30
-
如何计算参考输入作用下的稳态误差？详细阅读
下面分别讨论典型输入信号作用下控制系统的稳态误差。表3-1给出了各种系统类型在不同输入信号作用下系统的稳态误差。但是在计算系统稳态误差前，必须先判断系统的稳定性；其次开环增益K必须是在开环传递函数标准形式下，与式相似；该规律只适用于参考输入信号作用下的计算，其他信号作用下应用终值定理计算。......
2023-06-28
相关推荐