静定结构在支座移动时，只发生刚体位移，不产生内力和变形。这种位移可通过几何关系求得，也可应用单位力法进行计算。在式中，乘积的正负号规定为：当虚拟状态的支座反力与实际支座位移的方向一致时取正号，相反时取负号。 刚架的支座位移如图 5-19所示，试求 A 点的水平位移 ΔAx和 C 点左右截面的相对转角位移 θCC。......
2023-08-30
结构力学：组合结构与拱位移计算
【摘要】：计算结果为正，表示ΔCx的方向与所设单位力的方向相同，即 ΔCx方向向右。 求图 5-17所示半圆弧三铰拱顶铰 C 两旁截面的相对转角。图5-17解：计算拱的位移，仅考虑弯矩对弯曲变形的影响，按公式计算。计算三铰拱受荷载及单位力偶作用时［见图 5-17、］的弯矩方程，应先求出支座反力，然后列出弯矩方程。此题由于三铰拱为对称结构，可只对拱的一半列出方程。
1.组合结构
组合结构中有受弯为主的梁式杆和只承受轴力的链杆，因此，式（5-18）简化为
【例题5-6】 如图 5-15（a）所示组合结构在荷载作用下，已知链杆BE 的抗拉压刚度EA＝EI/4，其余受弯杆件抗弯刚度为EI，求 C 点的水平位移 ΔCx。
图5-15
解：（1）作实际状态的 MF图，如图 5-15（b）所示。
（2）建立虚拟状态，并作
图，如图 5-15（c）所示。
（3）进行图形相乘求位移 ΔCx。
计算结果为正，表示ΔCx的方向与所设单位力的方向相同，即 ΔCx方向向右。
2.曲杆和拱
对于曲杆和拱，如轴线的曲率较小，一般可采取像梁或刚架那样的处理方法。只有对较扁平的拱，由于轴力较大，轴向变形显著，才同时考虑轴向变形和弯曲变形两项影响。
【例题5-7】 图 5-16（a）所示是一半径为R 的等截面圆弧形悬臂曲梁，承受竖向均布荷载q，横截面的弯曲惯性矩为I，弹性模量为E，试求B 点的水平位移 ΔBx。
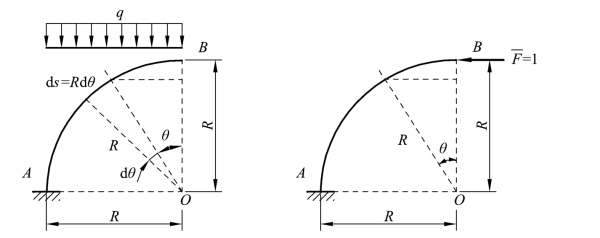
图5-16
解：计算该曲梁的位移，可采取像梁一样的处理方法，即仅考虑杆件由弯曲产生的弯曲变形影响，按公式（5-20）计算。在B 点加一单位水平力F=1，建立虚拟状态，如图 5-16（b）所示。由图可知，梁上对应于角度 θ 处的截面内，其弯矩可表示为
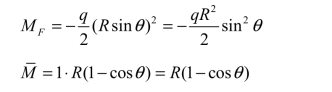
将以上两式代入（5-20）得
最后求得的位移是负的，表明该点位移的实际方向与虚单位力F=1的假设方向相反，即位移向右。
【例题5-8】 求图 5-17（a）所示半圆弧三铰拱顶铰 C 两旁截面的相对转角。圆弧半径为R，EI 为常数。只考虑弯矩对变形的影响。
图5-17
解：计算拱的位移，仅考虑弯矩对弯曲变形的影响，按公式（5-20）计算。在 C 点加一对单位力偶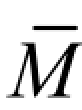
=1，建立虚拟状态，如图 5-17（b）所示。计算三铰拱受荷载及单位力偶作用时［见图 5-17（a）、（b）］的弯矩方程，应先求出支座反力，然后列出弯矩方程。此题由于三铰拱为对称结构，可只对拱的一半（BC）列出方程。
由图可知，拱上对应于角度 θ 处的截面内，其弯矩可表示为：
所以
有关结构力学的文章
- 详细阅读
-
结构力学中三铰拱内力计算攻略详细阅读
现以图 3-20所示的三铰拱为例说明其内力计算过程。图3-202.求任一截面 K 上的内力由于拱轴线为曲线，这使得三铰拱的内力计算较为复杂，但也可以借助其相应简支梁的内力计算结果，来求拱的任一截面K 上的内力。为了简便起见，在绘制三铰拱的内力图时，通常沿跨长或沿拱轴线选取若干个截面，求出这些截面上的内力值。表3-2三铰拱的内力计算......
2023-08-30
-
结构力学：组合结构概述详细阅读
组合结构是由承受弯矩、剪力和轴力的梁式杆和只承受轴力的链杆组成的结构。在组合结构中，利用链杆的受力特点，能较充分地利用材料，并从加劲的角度出发，改善了梁式杆的受力状态，因而组合结构广泛应用于建筑中的屋架、吊车梁以及桥梁中的承重结构等较大跨度的建筑物中。......
2023-08-30
-
结构力学：温度作用下的位移计算详细阅读
在使用时，这些结构所处的环境温度相对于建造时的温度一般要发生变化，这种温度的改变将会引起构件的变形，从而使结构产生位移。对于静定结构，温度改变只会引起材料的自由膨胀、收缩，在结构中不会引起内力，但将产生变形和位移。静定结构由于温度改变引起的位移计算公式，仍可由位移计算的一般公式导出。因此，点 C 的竖向位移为计算结果为负，表示 ΔCy的方向与所设单位力的方向相反，即 ΔCy向上。......
2023-08-30
-
结构力学：位移法概念简介详细阅读
位移法是以结构的结点位移作为基本未知量，取超静定的单个杆件及其组成的体系作为基本结构，通过平衡条件建立位移法方程，求出位移后，即可利用位移和内力之间的关系，求出杆件和结构的内力。通过下面简单例子具体说明位移法的基本原理和计算方法。综上所述，位移法的基本思路是“先固定后复原”。......
2023-08-30
- 详细阅读
-
合理拱轴概念的作用,结构力学详细阅读
求图 3-22所示三铰拱在竖向均布荷载q 作用下的合理拱轴。图3-22解：绘出拱的相应简支梁，如图 3-22所示，其弯矩方程为由式（3-3）可知，拱的水平推力为利用式（3-4），可求得合理拱轴的方程为由此可见，在满跨的竖向均布荷载作用下，对称三铰拱的合理拱轴为二次抛物线。需要指出，三铰拱的合理拱轴只是对一种给定荷载而言的，在不同的荷载作用下有不同的合理拱轴。......
2023-08-30
-
结构力学：线位移法数目确定详细阅读
在确定结点线位移的数目时，由于不计受弯直杆的轴向变形，并且假设弯曲变形是微小的，即认为直杆在受弯前后其投影长度保持不变。由于在确定结点线位移数目时，不计及杆件的轴向变形和弯曲变形，因此，可以先把所有的刚性结点和固定支座全部改成铰接，使结构变成一个铰接体系。结构基本未知量的总数等于结点的角位移数和线位移数之和。......
2023-08-30
相关推荐