“三相电路”图形符号主要包括字符和直线，其符号编码为S00005，主要应用于电路图、接线图和功能图中。下面介绍如何绘制该图形符号。图6-19 指定两个对角点图6-19 指定两个对角点图6-20 绘制一处字符组图6-20 绘制一处字符组操作技巧：要输入平方字符，则可在“文字编辑器”上下文选项卡的“插入”面板中单击“符号”按钮，接着从打开的符号下拉菜单中选择“平方”选项。图6-21 绘制另外一处字符组图6-21 绘制另外一处字符组......
2023-06-20
图形相乘法：结构力学教材
【摘要】：则有式就是图形相乘法的计算公式，应用该式进行计算时，除应满足前述三个条件外，还应注意以下两点：① 当MF图和图在杆的同侧时，乘积AyC为正号；在异侧时，AyC为负号。图中抛物线图形顶点处的切线均平行于基线，称为标准抛物线图形。图5-13进行图形相乘求位移ΔCy。
由例题 5-2 可知，应用公式（5-20）计算梁和刚架的位移时，须逐杆或逐段地进行积分运算。
当结构中杆件的数量较多或荷载情况比较复杂时，计算工作相当繁琐。但是，当结构中的各杆段满足以下三个条件：① 杆段的 EI 为常数；② 杆段的轴线为直线；③ 各杆段的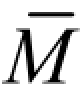
图和MF图中至少有一个为直线图。那么，就可用下述的图形相乘法代替积分运算，以简化计算。
对于等截面直杆，前两个条件自然满足。至于第三个条件，虽然在均布荷载的作用下MF图的形状是曲线形状，但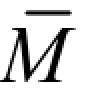
图却总是由直线段组成，只要分段考虑也可满足。于是，对于由等截面直杆段所构成的梁和刚架，在计算位移时均可应用图乘法。
若等截面直杆 AB 段的弯矩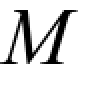
、MF图已经作出，如图 5-8 所示，其中MF图为任意形状，
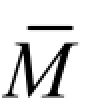图为一直线，M 图直线倾角为 α。若该杆的弯曲刚度EI 为一常数。
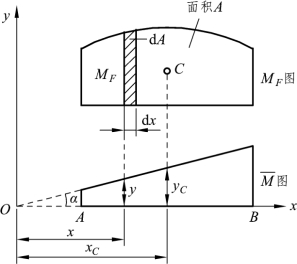
图5-8
由图可知，
图中某一点的纵坐标为：
= y =x tanα，代入式（5-20）中的积分式，则有
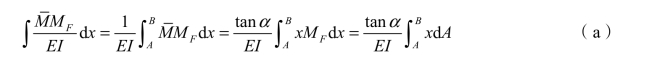
式中：dA＝MFdx，表示MF图的微面积（图 5-8 中阴影部分的面积）；
dx A表示MF图的面积A 对于y 轴的静矩，它可写成
式中，xC——MF图的形心C 到y 轴的距离。则有
式（5-21）就是图形相乘法的计算公式，应用该式进行计算时，除应满足前述三个条件外，还应注意以下两点：① 当MF图和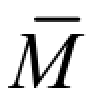
图在杆的同侧时，乘积AyC为正号；在异侧时，AyC为负号。② 纵坐标yC只能取自于沿着AB 的整个长度是一直线变化的图形。例如图 5-9（a）、（b）所示的直线变化图形中，沿杆长度不是一根直线，而是由两根直线所组成，图乘时必须分两段进行计算，然后相加。图 5-9（a）图乘结果为(A1y1+A2y2)/EI ，图 5-9（b）图乘结果为 A1y1/EI 。
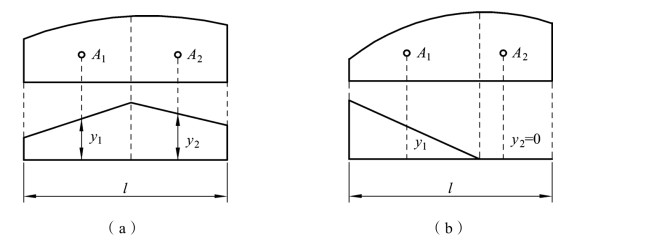
图5-9
图 5-10 中给出了几种常见简单图形的面积及其形心的位置。图中抛物线图形顶点处的切线均平行于基线，称为标准抛物线图形。
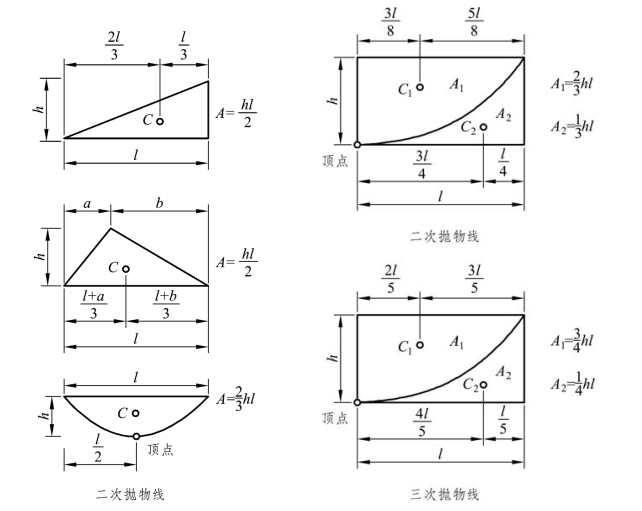
图5-10
当图形的面积和形心不便确定时，可将复杂的图形分解成几个简单的图形，然后分别将简单的图形相乘后再叠加。例如图 5-11（a）所示两个梯形相乘时，为了避免确定梯形面积形心位置的麻烦，可将梯形分解成两个三角形（或分解为一个矩形和一个三角形），然后相乘后叠加图乘结果为：
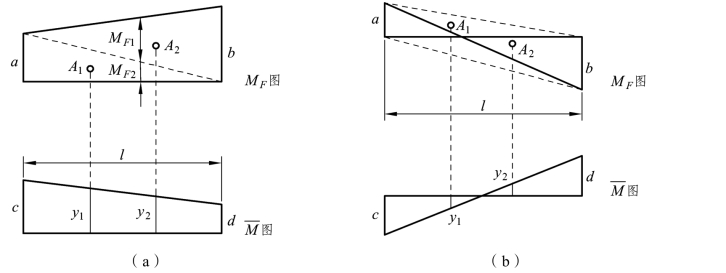
图5-11
式中：
对图 5-11（b）所示的图形，式（5-22）仍然适用，但式中各项正、负号必须根据同侧纵标相乘为正，异侧纵标相乘为负的原则确定。
下面举例来说明图乘法的实际应用。
【例题5-3】 求图 5-12（a）所示简支梁的中点 C 的竖向位移 ΔCy和 B 端截面的转角 θB。已知梁的EI 为常数。
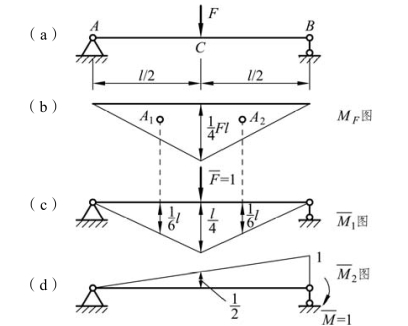
图5-12
解：（1）作实际状态的MF图，如图 5-12（b）所示。
（2）建立虚拟状态，并作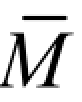
图。
计算梁中点 C 的竖向位移 ΔCy和B 端截面的转角θB的虚拟状态及相应的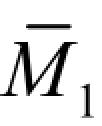
图、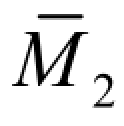
图，分别如图 5-12（c）、（d）所示。
（3）图乘求位移。
C 点的竖向位移 ΔCy：
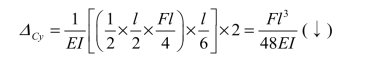
计算结果为正，表示ΔCy的方向与所设单位力的方向相同，即 ΔCy方向向下。
B 截面的转角：
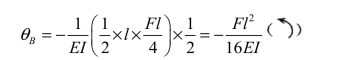
计算结果为负，表明θB的转向与所设单位力偶的转向相反，即θB为逆时针转向。
【例题5-4】 求图 5-13（a）所示外伸梁上点 C 的竖向位移 ΔCy。已知梁的EI 为常数。
解：（1）作实际状态的 MF图，如图 5-13（b）所示。
（2）建立虚拟状态，并作
图，如图 5-13（c）所示。
图5-13
（3）进行图形相乘求位移ΔCy。AB 段的MF图可以分解为一个三角形和一个标准抛物线形；BC 段的MF图则为一个标准抛物线形。MF图中各分面积与相应的
图中的竖标分别为
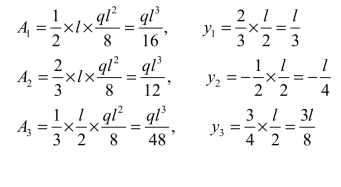
代入式（5-22）图乘，得C 点的竖向位移为
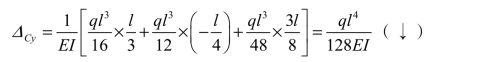
计算结果为正，表示ΔCy的方向与所设单位力的方向相同，即ΔCy向下。
【例题5-5】 求图 5-14（a）所示刚架C、D 两点之间沿CD 方向的相对位移ΔCD及C 截面的角位移θC，已知各杆的EI 为常数。
解：（1）作实际状态的 MF图，如图 5-14（b）所示。
（2）建立虚拟状态，并作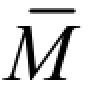
图。
求相对线位移 ΔCD、C 截面的角位移θC的虚拟状态及相应的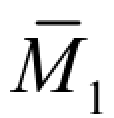
、
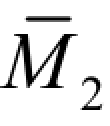图，分别如图 5-14（c）、（d）所示。
（3）进行图形相乘，求 ΔCD和θC。
图乘时，可将 AC 段和 CB 段的弯矩图分解成两部分。将图 5-14（b）、（c）进行图乘，得相对线位移 ΔCD为
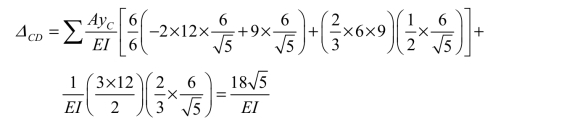
所得结果为正，表示C、D 两点之间的相对线位移与假设的一对单位力
=1的方向相同，即C、D 两点相互接近。
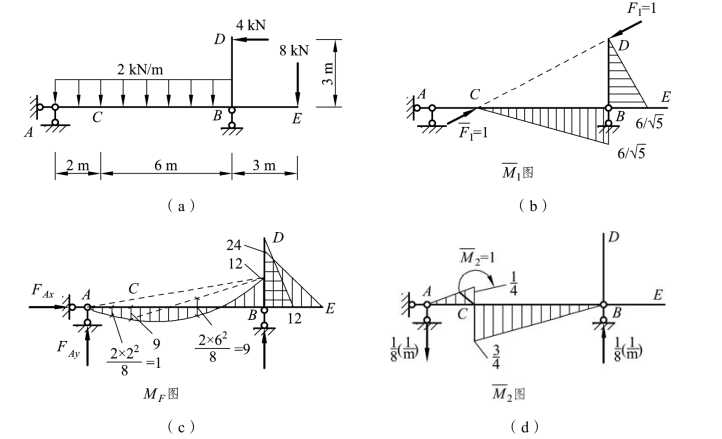
图5-14
将图 5-14（b）、（d）进行图乘，得 C 截面的角位移 θC为
所得结果为正，表示 C 点角位移与假设的一对单位力偶M2=1的方向相同。
有关结构力学的文章
- 详细阅读
-
图形软件生成图形的操作步骤详细阅读
步骤四，根据图形的具体要求选择软件界面上的可控参数，分别确定具体的q、w、x0、y0、s值。例1，选择对称斑图的QBColor模式分别生成条纹类以及块面构图图形。例2，选择非对称斑图的RGB模式生成斑图。其次，鼠标左击二级菜单中的RGB键，此时，在软件界面的Frame上方标识将出现“非对称斑图-RGB”的字样，见图1-6。如前所述，非对称斑图-RGB的“图形类型”对应了10个作图的子程序，可根据需要选用。......
2023-10-17
-
如何指定图形打印区域和预览图形？详细阅读
打印图形时,必须指定图形的打印区域。打印之前,可能会重新生成图形以重新计算范围。预览图形时,将隐藏活动工具栏和工具选项板,并显示临时的“预览”工具栏,其中提供打印、平移和缩放图形的按钮。在“打印”和“页面设置”对话框中,缩略预览还在页面上显示可打印区域和图形的位置。......
2023-06-20
-
运用图形编辑工具调整图形的具体方法详细阅读
在调整图形时需要运用图形编辑工具，即、、、、、命令。该命令使用的具体方法如下：1）运用拐角矩形工具绘制一长宽分别为5.00、3.00的图形。4）修剪完成后单击鼠标中键，退出命令，形成如图3-55所示图形特征。图3-54 拖动鼠标删除图3-55 删除段：在两线相交或延长后的相交处形成拐角，并删除拐角另一端的线。其具体做法如下：1）框选所要旋转的图形，单击组中的按钮，打开控制板并输入旋转角度与缩放比例分别为“45.000000、2.000000”，如图3-58所示。......
2023-06-19
-
相量及并联电路的电流相量图示例详细阅读
为了与一般复数相区别，我们把表示正弦量的复数称为相量。 已知两支路并联的正弦交流电路中，支路电流分别为i1=8sinA，i2=6sinA，试求总电流i，画出电流相量图。解：首先将各支路电流用最大值相量表示为则利用复数的加法运算法可得根据相量与正弦量之间的对应关系，即可写出根据相量与正弦量之间的对应关系，即可写出电流相量图如图4.2所示。电流相量图如图4.2所示。......
2023-06-24
-
结构力学：支座及支座反力详细阅读
只有竖向反力 FAy，根据可动铰支座的机动特征和受力特征，通常可简化为图 1-2所示一根垂直于支撑面的链杆。图1-22.固定铰支座固定铰支座，其构造如图 1-3所示，简称为铰支座，其约束特点是结构可绕铰 A转动，但沿水平和竖向的移动受到限制，此时，支座反力通过铰A 的中心，通常分解成水平和竖向的分反力FAx、FAy。......
2023-08-30
-
结构力学：位移法概念简介详细阅读
位移法是以结构的结点位移作为基本未知量，取超静定的单个杆件及其组成的体系作为基本结构，通过平衡条件建立位移法方程，求出位移后，即可利用位移和内力之间的关系，求出杆件和结构的内力。通过下面简单例子具体说明位移法的基本原理和计算方法。综上所述，位移法的基本思路是“先固定后复原”。......
2023-08-30
-
如何快速利用已有图形创建新图形？详细阅读
7）单击“确定”按钮，创建矩形阵列。图3-9环形阵列的含义创建环形阵列的操作步骤如下。图3-10环形阵列5）在“方法”下拉列表框中，选择下列方法之一，指定环形阵列的......
2023-09-18
相关推荐