首页理论教育简支梁的绝对最大弯矩和内力包络图-《结构力学》

简支梁的绝对最大弯矩和内力包络图-《结构力学》

2023-08-30 理论教育版权反馈

【摘要】：据此可以判断，在荷载组中部的几个集中荷载作用的截面，发生绝对最大弯矩的可能性最大。经验表明，在通常情况下产生简支梁绝对最大弯矩时的临界荷载 FK就是使跨中截面产生最大弯矩时的临界荷载。试求简支梁的绝对最大弯矩，并与跨中截面 C 的最大弯矩相比较。包络图分为弯矩包络图和剪力包络图。

1.简支梁的绝对最大弯矩

在移动荷载作用下，利用影响线可求出简支梁任意截面的最大弯矩，所有截面最大弯矩中的最大者称为绝对最大弯矩。对于等截面梁，发生绝对最大弯矩的截面为最危险截面，因此，绝对最大弯矩是简支梁（如吊车梁等）设计的依据。

如图4-18 所示的简支梁上作用有一组移动荷载，求此梁的绝对最大弯矩。

根据以往的计算经验，在集中荷载作用点处，弯矩图出现尖角。由此可知，绝对最大弯矩必定发生在某个集中荷载作用的截面上。而弯矩到达最大值的截面，其左、右截面剪力异号。据此可以判断，在荷载组中部的几个集中荷载作用的截面，发生绝对最大弯矩的可能性最大。

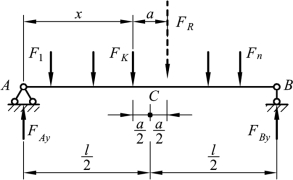
pagenumber_ebook=96,pagenumber_book=89

图4-18

如图4-18 所示，选定荷载组中部的某个集中荷载FK，设其作用点到支座A 的距离为x，梁上荷载组的合力 FR至 FK的距离为a，由平衡条件∑MB=0，得支座A 的反力为：

pagenumber_ebook=96,pagenumber_book=89

FK作用点的弯矩Mx为：

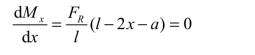
pagenumber_ebook=96,pagenumber_book=89

式中， pagenumber_ebook=96,pagenumber_book=89 为荷载 FK左侧梁上荷载对 FK作用点的力矩之和，它与 x 无关，由于荷载组中各荷载间距是不变的，所以是一个常量。当Mx为极大值时，根据极值的条件

pagenumber_ebook=96,pagenumber_book=89

得

pagenumber_ebook=96,pagenumber_book=89

这表明，当 FK与荷载组的合力 FR分别处在梁跨中点两侧对称位置时，集中荷载 FK作用点梁截面内的弯矩达到最大值。将式（4-8）代入式（4-7)，可得简支梁绝对最大弯矩的表达

式为

pagenumber_ebook=97,pagenumber_book=90

式（4-8）是根据 FK处于合力 FR的左侧得出的，如果 FK处于合力 FR的右侧，则上式中a 应以负值代入，a 是 FK与合力 FR之间的距离。另外，还应注意，在试算布排荷载位置时，若有荷载越出到梁外或进入到梁内时，一切都得重新计算，因为这时荷载组荷载的个数、合力的大小及其位置等都改变了。

经验表明，在通常情况下产生简支梁绝对最大弯矩时的临界荷载 FK就是使跨中截面产生最大弯矩时的临界荷载。这样就使问题得以简化。

【例题 4-6】某工厂吊车梁各跨均为简支梁，上面装有两台吨位相同的吊车，如图 4-19（a）所示。已知F1＝F2＝F3＝F4＝280 kN。试求简支梁的绝对最大弯矩，并与跨中截面 C 的最大弯矩相比较。

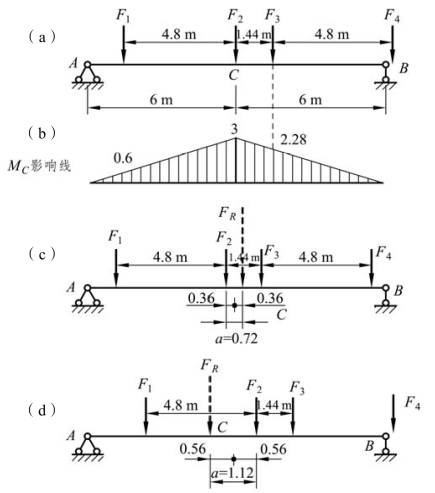
pagenumber_ebook=97,pagenumber_book=90

图4-19

解：根据已知条件，显然只有F2和F3可能是产生绝对最大弯矩的临界荷载。本例题中两吊车的轮距和压轮均相同，所以只需要选取其中一个集中荷载，如选取F2进行分析计算。

（1）求跨中截面 C 的最大弯矩。

使跨中截面C 产生最大弯矩的临界荷载。取F2在截面C 处时［见图4-19（a）］计算，绘制出MC的影响线，如图 4-19（b）所示，由此得

（2）确定最大弯矩。

① 梁上有 4 个荷载的情况。此时， FR位于 F2的右侧，将 F2和 FR对于梁中点C 对称布置［见图 4-19（c）］，则有

pagenumber_ebook=98,pagenumber_book=91

由此可求得 F2作用处的截面弯矩为

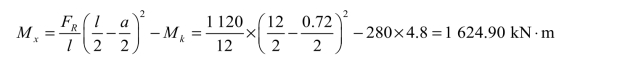
pagenumber_ebook=98,pagenumber_book=91

② 梁上只有 3 个荷载[见图 4-19（d）]。此时， FR位于 F2的左侧，对称于跨中截面C点布置，有

pagenumber_ebook=98,pagenumber_book=91

此时，由于 FR位于 F2的左侧，a 应为负值，取a＝－1.22，由此可求得 F2作用处的截面弯矩为：

pagenumber_ebook=98,pagenumber_book=91

比较以上两种情况可知，该梁在图示吊车移动荷载作用下的绝对最大弯矩Mx(max)为1 668.35 kN · m，它发生在图4-19 所示梁上只有 3 个荷载的情况下。

与跨中截面最大弯矩相比，绝对最大弯矩仅比跨中最大弯矩大 1.3%。在实际工作中，有时也用跨中截面的最大弯矩来近似代替绝对最大弯矩。

2.简支梁的内力包络图

由在恒载和活荷载共同作用下各截面内力的最大值连接而成的曲线，称为内力包络图。包络图由两条曲线构成，一条由各截面内力最大值构成，另一条由最小值构成，它是钢筋混凝土梁设计计算的依据。包络图分为弯矩包络图和剪力包络图。

作梁的弯矩（剪力）包络图时，可将梁沿跨度分成若干等份，利用影响线求出各等分点的最大弯矩（剪力）和最小弯矩（剪力），以截面位置作为横坐标，求得的内力值作为纵坐标，用光滑曲线连接各点即可得到包络图。

如图 4-20（a）所示为一跨度为 12 m 的吊车梁，承受两台同吨位吊车荷载，吊车传来的最大轮压为 82 kN，轮距为 3.5 m，两台吊车并行的最小间距为1.5 m。

将吊车梁分为十等份，分别计算在吊车荷载作用下各截面的最大、最小弯矩和剪力，即可绘出弯矩包络图，如图 4-20（b）所示；以及剪力包络图，如图 4-20（c）所示。

由以上可以看出，内力包络图是针对某种移动荷载而言的，对不同的移动荷载，内力包络图也不相同。

pagenumber_ebook=99,pagenumber_book=92

图4-20