在前一章所讨论的静定结构受力分析问题中,结构所受的荷载大小、方向及其作用位置都是确定的,这类荷载通常称为恒载。在单位移动荷载作用下,结构反力、内力或位移等随荷载位置变化的函数关系,分别称为反力、内力、位移的影响线方程,对应的函数图形分别称为反力、内力、位移的影响线。现以图 4-1所示简支梁为例,说明影响线的绘制过程。图4-1对于线性弹性结构,影响线是移动荷载作用下结构设计的重要工具。......
2023-08-30
影响线研究移动荷载作用时结构内力的变化,绘制影响线的主要目的是,应用影响线来确定移动荷载作用时对于某一量值的最不利影响,其用途主要有:① 在荷载位置已经确定的情况下,用来计算总的影响量值;② 在荷载位置未定的情况下,用来确定最不利的荷载位置。
1.应用影响线计算影响量
如果结构中某指定量值 S(可以是反力、内力等)的影响线已作出,可根据叠加原理利用影响线求出结构在各种固定荷载作用下的影响量值S。
(1)集中荷载作用下的影响量计算。
如图 4-9(a)所示,有一组集中荷载F1、F2、F3…Fn作用于确定的位置,设某量值 S(内力或反力)的影响线已绘出,与各荷载相对应的影响线纵标分别为 y1、y2、y3…yn,如图 4-9(b)所示。此时,集中荷载组所产生的总的影响量 S 可由叠加原理求得:

上式中,Fi向下为正,纵坐标yi在基线上为正,在基线下为负。
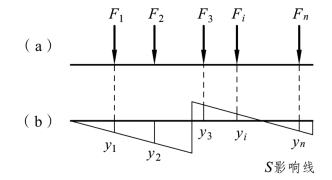
图4-9
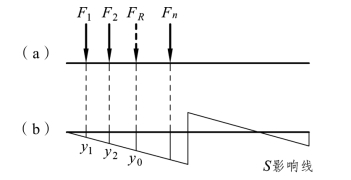
图4-10
当若干个集中荷载分布在影响线的同一条直线段时(见图 4-10),可根据合力矩定理来简化计算,用它们的合力来代替计算影响量。
![]()
式中,y0为合力FR位置对应的影响线的纵坐标。读者可仿图乘法推导思路证明上述结论。
(2)分布荷载作用下的影响量计算。
设在结构的某一段 AB 上作用有分布荷载 qx[见图 4-11(a)],利用S 影响线[见图 4-11(b)]来计算其影响量时,可将 qxdx 看作一个集中荷载,在影响线的AB 区段内积分可得

若是均布荷载[见图 4-12(a)],则有

式中A 代表均布荷载分布范围AB 段内的影响线面积,如图 4-12(b)中阴影部分所示,应取其代数和。
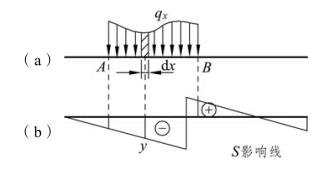
图4-11
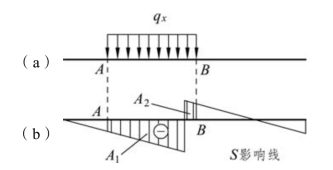
图4-12
因此,若要计算集中荷载组和分布荷载同时作用下的某一内力或反力,可叠加为
![]()
或为

【例题 4-4】 利用影响线求图 4-13(a)所示伸臂梁在图示载荷作用下 C 截面弯矩 MC和剪力 FSC的值。
解:(1)求弯矩MC,作出MC的影响线[见图 4-13(b)],可求得集中荷载对应的影响线的纵坐标,由叠加原理,得

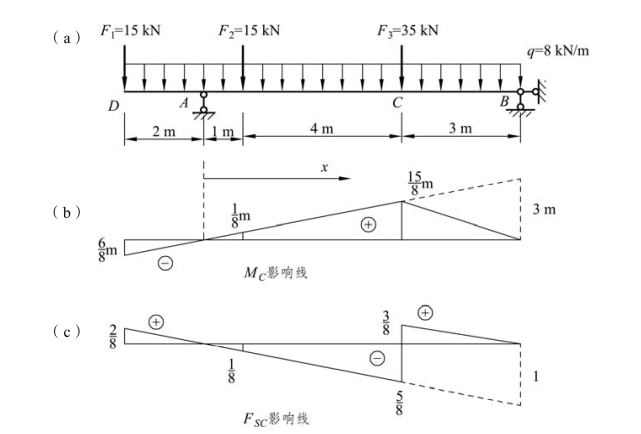
图4-13
2.确定最不利的荷载位置
如果荷载移动到某一个位置,使某量值 S 达到最大值,则此荷载位置称为该量值的最不利荷载位置。以在实际应用中较为常见的三角形形式的影响线为例,来说明确定最不利荷载位置的方法。
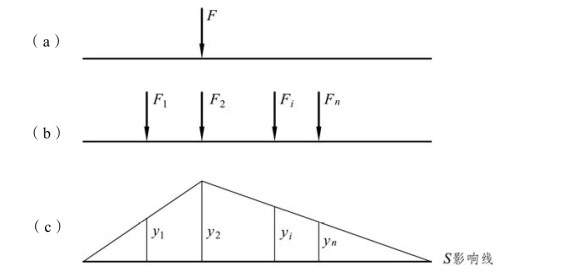
图4-14
(1)移动荷载组。
当S 的影响线为三角形时[见图 4-14(c)],如图 4-14(a)所示,如果移动荷载只有一个集中荷载,则根据式(4-1),使S 产生(正或负)最大值的最不利荷载位置,是这个集中荷载作用在影响线的纵坐标最大的三角形顶点位置处。然而,当有一组间距不变的集中荷载在梁上移动时[见图4-14(b)],则根据式(4-1),最不利荷载位置一般是数值较大且排列紧密的荷载位于影响线最大纵坐标处附近。要具体确定最不利荷载位置,首先要分析什么样的荷载作用位置可能使量值S 取得极值,这个荷载位置称为荷载的临界位置,然后再从这些临界位置中确定最不利位置。
图 4-15(a)表示一组间距不变的移动集中荷载,图 4-15(b)表示某一量值 S 的影响线。影响线两直线段的倾角分别为 α、β,均以逆时针方向为正,当荷载组移动一微小距离Δx 时,S 的变化量为
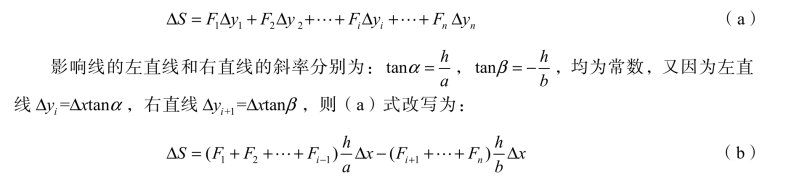
式(b)中,括号内分别代表作用于左直线和右直线部位的移动荷载。
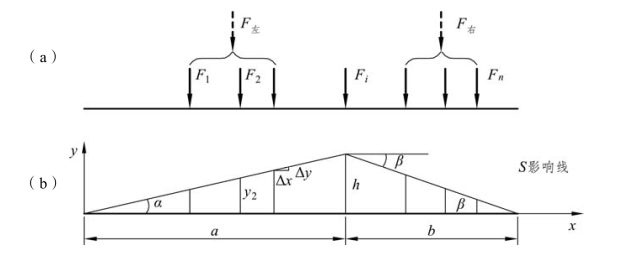
图4-15
量值S 取得极值的条件是当荷载组做微小移动时ΔS 发生变号。由式(b)可以看出,倘若在荷载移动过程中作用于左直线和右直线部位的荷载数量保持不变,则式(b)括号内将为常数,这样就不可能发生ΔS 变号的情况,或者说,要使ΔS 变号,就必须有一个集中荷载越过影响线的顶点。于是,我们得到一条重要的结论:在荷载总数不变时,量值S 取得极值的必要条件是有一个集中荷载恰好作用于影响线的顶点。
如果在荷载移动过程中ΔS 由正值转为负值,则量值S 取得一个极大值。假设S 取得极大值发生在某集中荷载 Fi作用于影响线顶点时,则该集中荷载便称为量值S 的一个临界荷载,记为 Fcr,其对应的荷载位置就称为临界位置,若以∑F左和∑F右分别表示 Fcr以左和以右的荷载之和,则由式(b)可得当为三角形影响线时,使量值S 取得极大值的临界荷载判别式为:

上式表明:临界位置的特点是有一集中荷载 Fcr作用于影响线的顶点,将 Fcr计入哪一侧(左侧或右侧),则哪一侧荷载的平均集度就大些。
利用式(4-6)虽可确定临界荷载,但有时临界荷载可能不止一个,此时可将相应的极值分别算出,其中最大的极值就是量值S 的最不利值,而相应的荷载位置即为移动荷载组的最不利位置。一般来说,S 的最不利值是在数值较大而又比较密集的集中荷载作用于影响线的顶点时发生的。因此,在按式(4-6)试算之前可先通过直观判断排除部分荷载,从而减轻计算工作。
综合以上内容,现将确定最不利荷载位置的步骤归纳如下:
① 最不利荷载位置一般是数值较大且排列紧密的荷载位于影响线最大纵标处的附近,由此判断可能的临界荷载。
② 将可能的临界荷载放置于影响线的顶点,判定此荷载是否满足式(4-6),若满足,则此荷载为临界荷载 Fcr,荷载位置为临界位置;若不满足,则此荷载位置就不是临界位置。
③ 对每个临界位置求出一个极值,然后从各个极值中选出最大值。与此相对应的荷载位置即为最不利荷载位置。
应当注意,在荷载向右或向左移动时,可能会有某一荷载离开了梁,在利用临界荷载判别式(4-6)时,∑F左和∑F右中应不包含已离开了梁的荷载。
(2)均布荷载。
如果移动荷载是长度不定、可以任意分布的均布荷载,则根据式(4-4),最不利荷载位置是在影响线[见图 4-16(a)]的正值部分布满荷载(求最大正值),如图 4-16(b)所示;或在负值部分布满荷载(求最大负值),如图 4-16(c)所示。
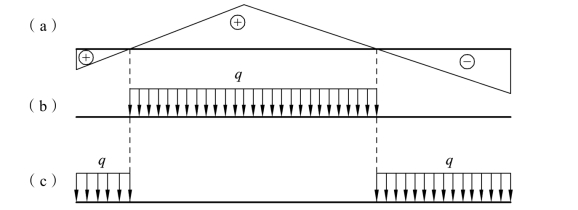
图4-16
【例题4-5】 试求图 4-17(a)所示吊车梁在图示吊车竖向荷载作用下B 支座的最大反力。设其中一台吊车轮压为 F1= F2=478.5 kN ,另一台吊车轮压为 F3= F4=324.5 kN ,轮距及车挡限位的最小车距如图所示。
解:先作出B 支座反力 FBy的影响线。由直观判断只有当 F2或 F3作用在影响线顶点时,FBy可能达到最大值。
先考虑 F2作用于B 点的情况[见图 4-17(b)],此时 F4已超出梁右端,有

故 F2是临界载荷。此时,有
![]()
再考虑 F3作用于 B 点的情况[见图 4-20(c)],此时 F1已超出梁左端,有

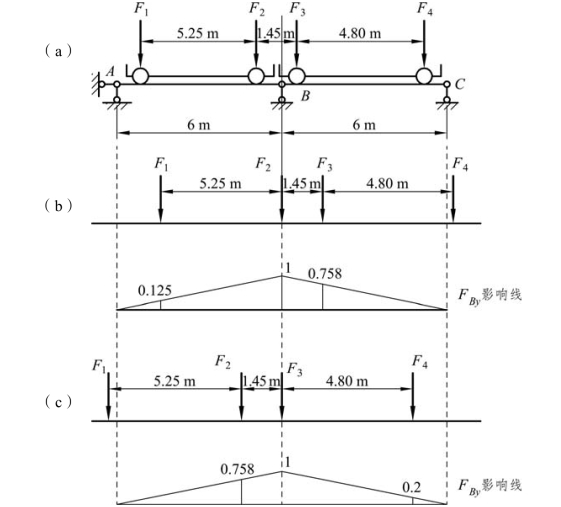
图4-17
故 F3也是临界荷载。此时有
![]()
比较以上两者可知,当 F2作用于B 点时为最不利荷载位置,相应B 支座的最大反力FBymax为784.3 kN。
有关结构力学的文章

在前一章所讨论的静定结构受力分析问题中,结构所受的荷载大小、方向及其作用位置都是确定的,这类荷载通常称为恒载。在单位移动荷载作用下,结构反力、内力或位移等随荷载位置变化的函数关系,分别称为反力、内力、位移的影响线方程,对应的函数图形分别称为反力、内力、位移的影响线。现以图 4-1所示简支梁为例,说明影响线的绘制过程。图4-1对于线性弹性结构,影响线是移动荷载作用下结构设计的重要工具。......
2023-08-30

图4-5间接荷载作用下的各项影响线,可由直接荷载作用时的影响线加以修正而得。由此可知,只需找到直接荷载作用下的MK影响线的各结点处的纵坐标,再将相邻纵坐标连以直线即可得到间接荷载下的MK的影响线。修正的范围通常是需求量值的区段、支座两边的区段和有铰的区段,即两横梁间的影响线不是直线的均需修正。并可知,不论截面D 位于C、E 两点之间任何一处,FSD的影响线都是一样的。......
2023-08-30

圆台Ⅰ与半圆柱体Ⅲ相交,相贯线的左视图为圆弧5"4"6",利用辅助平面法求出这段相贯线的主视图和俯视图。图5-20补相贯线分析形体分析。分析外表面的相贯线。圆柱体Ⅱ的上半部分与半球相交,得到特殊相贯线——圆,主、俯视图为一直线段。两圆柱孔的轴线垂直相交,直径相等,为一特殊相贯线,正面投影积聚成直线段。......
2023-06-28

下面结合三次超静定的刚架来进一步说明用力法解多次超静定结构的一般原理和力法典型方程的建立。上述方程组在组成上具有一定的规律性,不论超静定结构的类型、超静定次数以及所选的基本结构如何,所得的方程都具有式(6-2)的形式,故称之为力法的典型方程。力法方程最后一项位移 ΔiF称为自由项。......
2023-08-30

在确定结点线位移的数目时,由于不计受弯直杆的轴向变形,并且假设弯曲变形是微小的,即认为直杆在受弯前后其投影长度保持不变。由于在确定结点线位移数目时,不计及杆件的轴向变形和弯曲变形,因此,可以先把所有的刚性结点和固定支座全部改成铰接,使结构变成一个铰接体系。结构基本未知量的总数等于结点的角位移数和线位移数之和。......
2023-08-30

剪力分配法是适用于铰接排架和横梁为刚性杆、竖柱为弹性杆的有侧移刚架的计算。这种利用剪力分配系数求柱顶剪力的方法称为剪力分配法。对于图8-15 所示横梁刚度为无限大的刚架,柱顶作用水平荷载,结点角位移为零,只有一个独立结点线位移,故同样可采用剪力分配法进行计算。图8-18解:计算剪力分配系数。......
2023-08-30

利用组成几何不变体系的基本规则,可以组成各种各样的几何不变体系,也可以利用这些规则对已有的体系进行几何组成分析。下面将通过具体的例子来说明平面体系的几何组成分析。两刚片由铰 C 和杆 IJ 连接,根据规则 2 可知,体系为几何不变体,且无多余约束,作为一个大刚片。 试对图 2-16所示体系做几何组成分析。如果铰B 和虚铰O1、O2不在同一条直线上,则此体系为无多余约束的几何不变体系;如果此三铰在同一条直线上,则为瞬变体系。......
2023-08-30

热喷涂技术在冶金机械中的应用历史较长,技术比较成熟。近年来,随着冶金制造技术水准的不断提高,速度、效率要求越来越高,新的涂层材料、涂层制备工艺技术正在逐步扩展在冶金工业中的应用。钢铁冶金设备中热喷涂技术的应用见表6-7。表6-7 钢铁冶金设备中热喷涂技术的应用(续)1.高炉渣口、风口基体材料为纯铜或铸锡青铜,长期承受高温气体的冲蚀及熔渣、铁液的冲刷,主要破坏形式是烧蚀。该工艺技术镀锌生产中已普遍采用。......
2023-06-18
相关推荐