用静力法作影响线，需要先求影响线方程，而后才能作出相应的图形。当结构较复杂时，用静力法就更加烦琐，而且工程上有时只需画出影响线的轮廓即可，这时常采用机动法作影响线。机动法的理论基础是刚体的虚功原理。虚位移图即代表了RB影响线的形状，如图16-5所示。使AC、CB沿MC正向发生相对单位转角1，得到图16-6所示的位移图，即MC的影响线。C点影响线的值可以根据这个条件，按几何比例求得。......
2023-08-26
通过静力法计算静定梁的影响线效果
【摘要】：在用静力法作一些常见结构反力及内力的影响线时，需要注意的是：正确的影响线应该具有“正确的外形、必要的控制点纵坐标值和正负号”。下面就以图 4-2所示双伸臂梁为例，来进一步说明用静力法作静定梁的反力和内力影响线的方法。故影响线方程应分别考虑。对于多跨静定梁，只需要分清它的基本部分和附属部分及这些部分之间的传力关系，再利用单跨静定梁的已知影响线，即可顺利绘出多跨静定梁的影响线。
利用结构在单位移动荷载F＝l 作用下的静力平衡条件（对静定结构用平衡条件，对于超静定结构用力法、位移法等），建立所求某量值与荷载位置间的函数关系式，即影响线方程，然后由方程作出影响线。这一方法称为静力法。具体步骤为：
（1）确定坐标系，以坐标x 表示荷载 F＝1 的位置。
（2）将x 看成是不变的，F＝1 看成是固定荷载，确定所求量的值，即可得影响线方程。
（3）按影响线方程作出影响线并标明正负号和控制点的纵坐标值。
在用静力法作一些常见结构反力及内力的影响线时，需要注意的是：正确的影响线应该具有“正确的外形、必要的控制点纵坐标值和正负号”。内力正负号规定与第3 章相同，但习惯上将纵标为正的影响线绘于基线上方且注明正负号。
下面就以图 4-2（a）所示双伸臂梁为例，来进一步说明用静力法作静定梁的反力和内力影响线的方法。
1.反力影响线
取梁的左边支座 A 为坐标原点，以x 表示F＝1 的作用位置，如图 4-2（a）所示，设反力向上为正。当荷载F＝1 在梁上 AB 间任一位置时，根据平衡方程∑MB=0，可得影响线方程
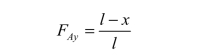
由影响线方程可作出反力FAy的影响线，如图 4-2（b）所示。
同理，根据平衡条件得：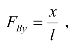
作出 FBy的影响线，如图 4-2（c）所示。
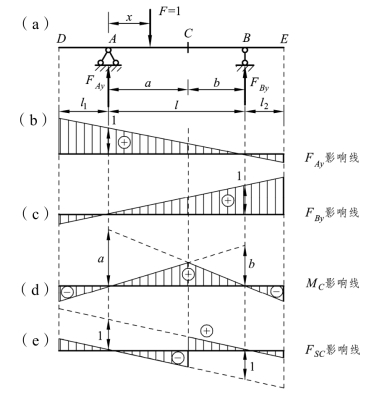
图4-2
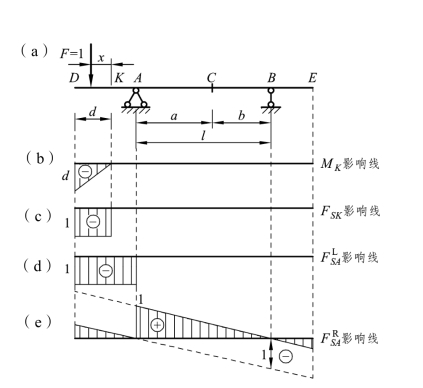
图4-3
2.跨内截面内力的影响线
现在绘制如图 4-2（a）所示梁截面C 上内力的影响线。
取C 点左侧部分或右侧部分为隔离体，由隔离体的平衡求C 截面剪力FSC和弯矩MC。由于单位荷载是移动的，既可在C 点左侧，也可在C 点右侧。故影响线方程应分别考虑。
当单位荷载在C 点左侧时，即 0≤x＜a，取右侧为隔离体（取左侧也可以），由隔离体平衡，有：
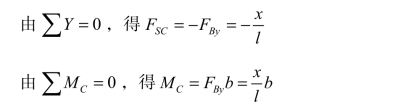
当单位荷载在 C 点右侧时，即a＜x≤l，取左侧为隔离体，有
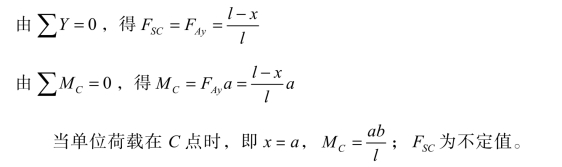
根据以上影响线方程即可作出剪力FSC和弯矩MC的影响线，如图 4-2（d）、（e）所示。由弯矩的影响线方程可知弯矩影响线MC的量纲为L。
由上面计算过程可见：当0≤x＜a 时，MC的影响线与FBy的影响线形状相同，竖标相差b倍，而FSC与FBy只相差符号。当a＜x≤l 时，MC的影响线与FAy影响线的形状相同，竖标相差 a 倍，而 FSC与 FAy相同。即MC和FSC的影响线可由FAy和FBy影响线导出。因此，反力影响线是基本影响线，而弯矩和剪力影响线是导出影响线。
3.伸臂部分截面内力的影响线
同样，根据静力平衡条件，可绘制出如图 4-3（a）所示伸臂部分截面的弯矩MK的影响线和剪力FSK的影响线，以及A 支座左、右截面剪力
、
的影响线，分别如图 4-3所示。
以上我们分别介绍了静定梁的反力、跨内及伸臂部分截面的弯矩和剪力等各种具有典型性的影响线，它们都有各自的特点。掌握这些特点，一般只需求出几个特殊点的纵坐标，就能把影响线作出来了，而无须列出方程。为了更好地理解影响线，请自行总结影响线和恒载下内力图的区别。
对于多跨静定梁，只需要分清它的基本部分和附属部分及这些部分之间的传力关系，再利用单跨静定梁的已知影响线，即可顺利绘出多跨静定梁的影响线。
【例题4-1】 试用静力法作图 4-4（a）所示多跨静定梁中的反力及FBy和内力MK，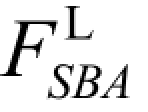
，FSm，Mn，MD等影响线。
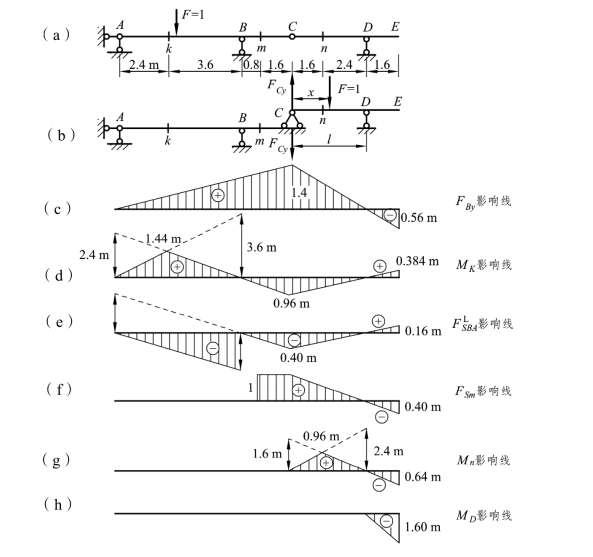
图4-4
解：这是一多跨静定梁，其中 AC 是基本部分（伸臂梁），CE 则为附属部分，其关系图如图 4-4（b）所示。若要作出基本部分中的影响线，那么当单位荷载在AC 段移动时，需作出的就是伸臂梁的影响线；当单位荷载在CE 段内移动时，由于影响线应该是直线，因此，只要取两点的值即可，一般取 C 点和 D 点的值。因为 C 点的值已知，而 D 点的值等于零（很容易判断出来）。 FBy、MK、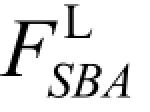
、 FSm等的影响线，如图 4-4（c）、（d）、（e）、（f）所示。
要作出图 4-4（a）中附属部分的Mn、MD的影响线，当单位荷载在 AC 段移动时，Mn、MD的值为零，即该部分没有影响线；当单位荷载在CE 段移动时，由于该部分也是伸臂梁，按伸臂梁画出的影响线即可。Mn、MD的影响线如图 4-4（g）、（h）所示。
有关结构力学的文章
- 详细阅读
-
用机动法对静定梁的影响线进行分析详细阅读
用机动法绘制静定梁的影响线，把绘制支座反力或内力影响线的静力问题转化为绘制位移图的几何问题。用机动法作反力影响线，首先必须解除相应的反力约束，把反力当作外力。此外，也可用机动法来校核用静力法所作的影响线。 用机动法绘制图 4-8所示多跨静定梁MB、FSF、FSC、FBy、MG的影响线。由于本题是多跨静定梁，解除一个约束后成为单自由度体系，因此体系所产生的刚体虚位移图就是要作的影响线。......
2023-08-30
-
用位移法计算连续梁与超静定刚架详细阅读
位移法计算连续梁及超静定刚架一般步骤如下：确定基本未知量和基本结构。用位移法计算时，只有节点转角基本未知量，故仅需建立刚节点处的力矩平衡方程，即可求解出全部未知量，进而计算杆端弯矩，绘制出内力图。此连续梁只有一个刚节点B的转角位移θB，如图15-32所示。列各杆杆端弯矩计算式。用位移法计算图15-34所示的超静定刚架，并作出弯矩图。......
2023-08-26
-
用力法求解超静定梁的方法和步骤详细阅读
计算超静定梁的位移时，通常忽略轴力和剪力的影响，只考虑弯矩的影响。因而系数及自由项按照下列公式计算：试用力法作图14-13所示单跨超静定梁的弯矩图。此梁具有三个多余约束，为三次超静定。将以上各值代入力法方程，而在前两式中消去后，得解以上方程组求得由力法方程的第三式求解X3时，可以看出，按不同的假设有不同的结果。......
2023-06-16
-
3.2结构力学：多跨静定梁的内力计算详细阅读
图3-6多跨静定梁是由若干单跨静定梁相互用铰连接起来的，通常有两种基本形式。图3-82.多跨静定梁的内力计算从受力分析来看，由于基本部分直接与地基组成几何不变体系，因此它能独立承受荷载而维持平衡。......
2023-08-30
-
梁的计算简图与静定基本形式详细阅读
固定铰支座限制支承处沿任何方向的线位移，因此，相应支座反力可用两个分力表示，例如水平反力与垂直反力。一端或两端向外伸出的简支梁，称为外伸梁。以上三种梁的支座反力只有三个，可由静力平衡方程完全确定。这类仅用平衡方程即可求出全部未知反力的梁称为静定梁。图7-8梁的基本形式......
2023-06-19
-
力法应用：建筑力学（第3版）计算超静定梁内力详细阅读
根据上述力法原理，用力法计算超静定结构内力的计算步骤如下：去掉原结构的多余约束并代之以多余未知力，选取基本体系。试用力法计算图15-12所示超静定梁的内力，并绘制出弯矩图。由基本体系在多余未知力X1及荷载的共同作用下，B点处沿X1方向上的位移等于零的变形条件，建立力法方程为计算方程中的系数和自由项。因此，它的弯矩图与同跨度、同荷载的简支梁相比较，最大弯矩峰值较小，使整个梁上内力分布得以改善。......
2023-08-26
-
如何设计多跨静定梁结构？详细阅读
在实际的建筑工程中，多跨静定梁常用来跨越几个相连的跨度。图12-9桥梁在房屋建筑结构中的木檩条[图12-10]，也是多跨静定梁的结构形式。图12-10木檩条从几何组成来看，多跨静定梁可分为基本部分和附属部分。但是从整体看，多跨静定梁是几何不变的，也是静定的。因此，一般来说，多跨静定梁的弯矩比一列简支梁的弯矩小，所用材料较为节省。但是，多跨静定梁的构造较为复杂。......
2023-06-16
相关推荐