结构力学中的影响线绘制方法及其重要性

2023-08-30 理论教育版权反馈

【摘要】：在前一章所讨论的静定结构受力分析问题中，结构所受的荷载大小、方向及其作用位置都是确定的，这类荷载通常称为恒载。在单位移动荷载作用下，结构反力、内力或位移等随荷载位置变化的函数关系，分别称为反力、内力、位移的影响线方程，对应的函数图形分别称为反力、内力、位移的影响线。现以图 4-1所示简支梁为例，说明影响线的绘制过程。图4-1对于线性弹性结构，影响线是移动荷载作用下结构设计的重要工具。

在前一章所讨论的静定结构受力分析问题中，结构所受的荷载大小、方向及其作用位置都是确定的，这类荷载通常称为恒载。在恒载作用下结构的支座反力和内力都固定不变。但有些工程结构要承受的荷载，其作用位置是移动的，例如在桥梁上行驶的火车和汽车、在吊车梁上行驶的吊车等，这类荷载称为移动荷载。所谓移动荷载，是指大小、方向不变，而作用位置随时间变化的荷载。例如图 4-1（a）所示的简支梁，随着车辆的行驶，车辆的轮压力［见图 4-1（b）］F1、F2的作用位置随之变化，支座反力FAy逐渐减小，而FBy却逐渐增大。可见结构在移动荷载作用下，其反力、内力及位移是随着移动荷载位置的改变而变化的。因此，必须研究静定结构在移动荷载作用下反力、内力（以下统称为某量值）的变化规律，确定其最大值，以及达到最大值时荷载的位置，从而为结构设计提供依据。

结构实际可能承受的移动荷载是多种多样的，如桥梁所受的移动荷载可能是行驶中的一辆汽车或一个车队，也可能是火车或履带式车辆等。所受荷载不同，反力、内力以及位移等随荷载作用位置变化的规律自然也不同。为解决结构在不同移动荷载作用下的计算，基于线性弹性结构的叠加原理，可先研究结构在一个最简单的移动荷载，即单位移动荷载（F＝1）在结构上移动时，给定截面上某种量值 S（称为影响量）的变化规律，然后利用叠加方法计算其他较复杂移动荷载作用时，该量值的变化规律以及最不利的荷载位置等。

在单位移动荷载作用下，结构反力、内力或位移等随荷载位置变化的函数关系，分别称为反力、内力、位移的影响线方程，对应的函数图形分别称为反力、内力、位移的影响线。

现以图 4-1（c）所示简支梁为例，说明影响线的绘制过程。以 A 为坐标原点，以x 表示单位移动荷载F＝1 的作用位置，设支座反力FAy、FBy向上为正。由平衡条件∑MA=0，可得：

pagenumber_ebook=81,pagenumber_book=74

由此可知，反力FBy是单位移动荷载位置坐标x 的函数。当x 变化时，就意味着单位移动荷载F＝1 在梁上移动。所以式（a）就是反力FBy关于单位移动荷载F＝1 的影响线方程，以水平基线为横坐标x，表示单位移动荷载F＝1 的作用位置，纵坐标 y 表示相应的FBy值，作出这个方程的图形，即为反力FBy的影响线，如图 4-1（d）所示。由（a）式可知反力FBy的量纲为 1。

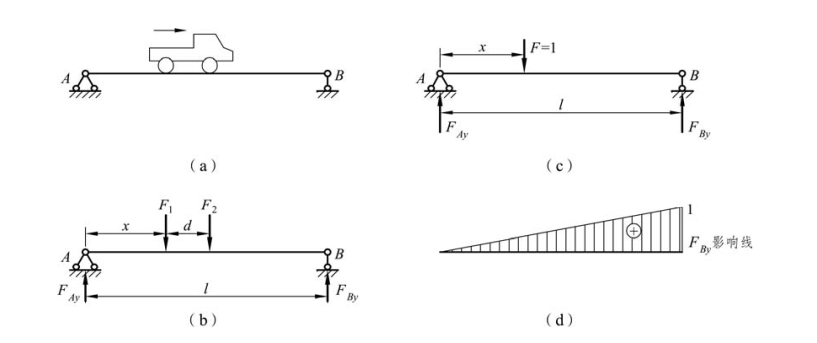
pagenumber_ebook=82,pagenumber_book=75

图4-1

对于线性弹性结构，影响线是移动荷载作用下结构设计的重要工具。

作结构上某量值的影响线有两种基本方法：静力法和虚功法，虚功法也称为机动法。

结构力学中的影响线绘制方法及其重要性

相关推荐