杆件轴线及荷载作用线均处在同一平面内的刚架，称为平面刚架。在工程中实际应用的刚架，多数是超静定的，静定刚架较少采用。图3-112.静定平面刚架计算静定刚架的内力通常有弯矩、剪力和轴力，其计算方法原则上与静定梁的计算相同。......
2025-09-30
结构力学习题：计算静定梁的M图、铰C处力和轴线切线夹角
【摘要】：图3-452. 如图 3-46 所示，试不经过计算反力绘制出多跨静定梁的 M 图。已知三铰拱的拱轴线方程为：求水平推力。求铰 C 处的剪力和轴力。求集中力作用处轴线切线与水平轴的夹角。
1. 计算图 9-9 所示连续梁的结点转角和杆端弯矩。
图9-9
2. 试用矩阵位移法计算图 9-10 所示连续梁。EI＝常数。
图9-10
3. 用矩阵位移法计算图 9-11 所示结构（不计轴向变形），并绘制弯矩图。
4. 用矩阵位移法计算图 9-12 所示结构（不计轴向变形），并绘制弯矩图。
5. 用矩阵位移法计算图 9-13 所示刚架（不计轴向变形），并绘制弯矩图、剪力图和轴力图。
图9-11(https://www.chuimin.cn)
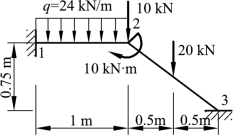
图9-12
图9-13
6. 用矩阵位移法计算图 9-14 所示刚架（不计轴向变形），并绘制弯矩图。
7. 试用矩阵位移法计算图 9-15 所示桁架各杆的轴力，设各杆 EA/L 相同。
图9-14
图9-15
相关文章
- 详细阅读
-
力法应用：建筑力学（第3版）计算超静定梁内力详细阅读
根据上述力法原理，用力法计算超静定结构内力的计算步骤如下：去掉原结构的多余约束并代之以多余未知力，选取基本体系。试用力法计算图15-12所示超静定梁的内力，并绘制出弯矩图。由基本体系在多余未知力X1及荷载的共同作用下，B点处沿X1方向上的位移等于零的变形条件，建立力法方程为计算方程中的系数和自由项。因此，它的弯矩图与同跨度、同荷载的简支梁相比较，最大弯矩峰值较小，使整个梁上内力分布得以改善。......
2025-09-30
-
力法方程计算基本结构位移，图1.8-2和M1详细阅读
原结构变为图1.8-1c，其中X1为多余约束中产生的约束力。图1.8-1 基本结构2.力法方程基本结构在B点的竖向位移必须为零，即δ11X1+Δ1p=0 式中，δ11为基本结构在X1=1作用下沿X1的指向引起的位移；Δ1p为基本结构在荷载P作用下沿X1的指向引起的位移。方程称为力法方程。但是，在力法分析中采用以下叠加公式计算M，即图1.8-2 Mp图和M1图上述公式对结构上的任何点均适用。......
2025-09-30
-
结构力学中三铰拱内力计算攻略详细阅读
现以图 3-20所示的三铰拱为例说明其内力计算过程。图3-202.求任一截面 K 上的内力由于拱轴线为曲线，这使得三铰拱的内力计算较为复杂，但也可以借助其相应简支梁的内力计算结果，来求拱的任一截面K 上的内力。为了简便起见，在绘制三铰拱的内力图时，通常沿跨长或沿拱轴线选取若干个截面，求出这些截面上的内力值。表3-2三铰拱的内力计算......
2025-09-30
-
梁的计算简图与静定基本形式详细阅读
固定铰支座限制支承处沿任何方向的线位移，因此，相应支座反力可用两个分力表示，例如水平反力与垂直反力。一端或两端向外伸出的简支梁，称为外伸梁。以上三种梁的支座反力只有三个，可由静力平衡方程完全确定。这类仅用平衡方程即可求出全部未知反力的梁称为静定梁。图7-8梁的基本形式......
2025-09-29
-
用位移法计算连续梁与超静定刚架详细阅读
位移法计算连续梁及超静定刚架一般步骤如下：确定基本未知量和基本结构。用位移法计算时，只有节点转角基本未知量，故仅需建立刚节点处的力矩平衡方程，即可求解出全部未知量，进而计算杆端弯矩，绘制出内力图。此连续梁只有一个刚节点B的转角位移θB，如图15-32所示。列各杆杆端弯矩计算式。用位移法计算图15-34所示的超静定刚架，并作出弯矩图。......
2025-09-30
-
用力法求解超静定梁的方法和步骤详细阅读
计算超静定梁的位移时，通常忽略轴力和剪力的影响，只考虑弯矩的影响。因而系数及自由项按照下列公式计算：试用力法作图14-13所示单跨超静定梁的弯矩图。此梁具有三个多余约束，为三次超静定。将以上各值代入力法方程，而在前两式中消去后，得解以上方程组求得由力法方程的第三式求解X3时，可以看出，按不同的假设有不同的结果。......
2025-09-29
- 详细阅读
相关推荐