平面汇交力系可以建立两个独立的平衡方程，解算两个未知量。继续取8、6、7等结点为隔离体，可求得桁架右半边各杆的内力。图12-30桁架轴力示意在桁架内力计算时，往往会遇到内力为零的杆件，这种杆件称为零杆。计算桁架的内力宜从几何分析入手，以便选择适当的计算方法，灵活地选取隔离体和平衡方程。除结点法外，计算桁架内力的另一基本方法是截面法。截面法适用于联合桁架的计算以及简单桁架中求少数指定杆件内力的情况。......
2023-06-16
静定平面桁架内力计算的步骤
【摘要】：应用结点法计算桁架内力时，常会遇到一些特殊的结点，可以根据节点的平衡条件判定桁架中某些杆件的轴力为零，或者可以判定与某一结点相连的两杆内力数值相等，从而使计算得以简化。截面法是用适当的截面，截取桁架中包含两个以上结点的部分为隔离体。因此，由平衡条件3.结点法和截面法的联合应用结点法和截面法是计算桁架内力
桁架内力的计算方法，主要有结点法和截面法。除此之外，根据各种桁架的不同组成特点，灵活运用这两种基本方法，将结点法和截面法联合应用更为方便。
1.结点法
如果桁架完全符合前述的三点假定，则其每根杆件只承受轴力，而无弯矩和剪力。这样，桁架的每个结点都构成一个汇交力系。取桁架的结点作为隔离体，利用平面汇交力系的静力平衡条件，计算桁架内力的方法，就称为结点法。
作用于平面桁架任一结点的各力（包括荷载、支座反力和杆件轴力）组成一平面汇交力系，就每一个结点可以列出两个平衡方程，对于有n 个结点的平面桁架可以列出2n 个平衡方程，其数量恰好等于静定平面桁架的链杆(包括支座链杆)约束数目。因此，从原则上讲，联立求解上述2n 个平衡方程，就可以求得桁架所有杆件的轴力和支座反力。
为了避免解联立方程，对于简单桁架，是由基础或由三杆组成的基本三角形出发，根据每增加两根杆件 (两个未知力）和新增添一个结点（两个平衡方程）的二元片组成规则，逐次扩展形成的。因此，应用结点法计算简单桁架的内力时，如能利用这一规律，从其最后形成的一个结点开始，循着各结点形成顺序的相反顺序，逐次应用结点法，则每次得到的平衡方程中，至多不会超过两个未知力，依次进行可求得桁架所有杆件的内力。
【例题3-7】 用节点法计算图 3-28（a）所示桁架中各杆的轴力。
解：（1）先求支座反力。
由于桁架及荷载对称，则： F1y=120 kN ， F8y=120 kN 。
（2）求内力。由于对称性，只求出半边即可（如左半边），则另一半边位于对称位置的各杆与其内力相同。
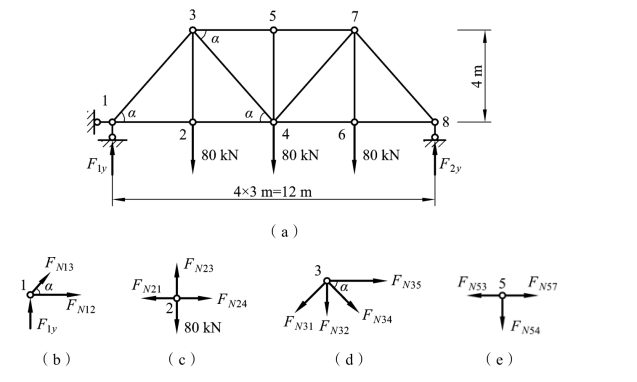
图3-28
由几何关系可得：
取 1 结点为隔离体［见图 3-28（b）］：
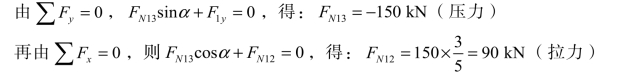
取2 结点为隔离体［见图 3-28（c）］：
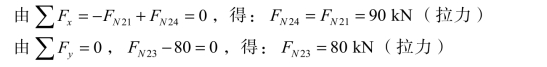
取3 结点为隔离体［见图 3-28（d）］：
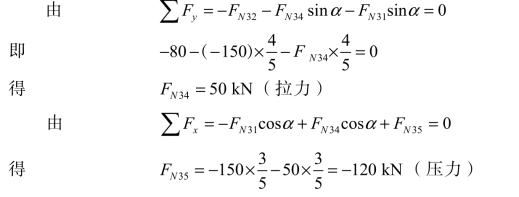
由对称性可得另一半边各杆内力。
取4 结点为隔离体［见图3-28（e）］：
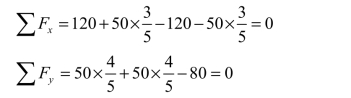
可见计算无误。最后可将各杆件轴力值及其正负标注在相应的杆件旁。
在上例中，杆54 内力FN54= 0，桁架中轴力为零的杆件称为零杆。
应用结点法计算桁架内力时，常会遇到一些特殊的结点，可以根据节点的平衡条件判定桁架中某些杆件的轴力为零，或者可以判定与某一结点相连的两杆内力数值相等，从而使计算得以简化。这几种特殊情况如下：
（1）不共线的两杆结点上无荷载作用时［见图 3-29（a）］，则两杆均为零杆。
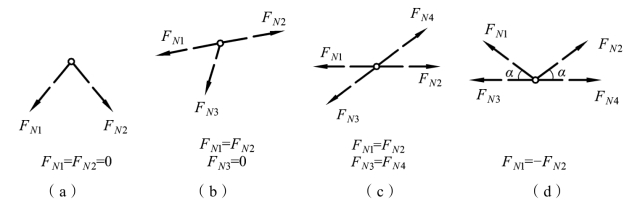
图3-29
（2）两杆共线的三杆件结点上无外力作用时［见图 3-29（b）］，共线的两根杆轴力相等，另一根为零杆。
（3）两两共线的四杆结点（X 形结点）上无荷载作用时［见图 3-29（c）］，则处在同一直线上的两杆内力相等。
（4）两杆共线而另外两杆在直线同侧，且交角相等的四杆结点（K 形结点）上无荷载作用时［见图 3-29（d）］，处在直线同一侧边的两杆内力等值而反向。
上述结论，根据各结点的平衡条件均可证实，读者可自行证明。
对于图 3-30（a）所示的桁架，结点F 符合上述情况（1），因而有FNFE=FNFB=0；结点D 符合情况（2），因而有FNDH=0；结点G、I 的情况类似于情况（3），有FNGA=FNGH、FNGC=F 、FNIE=F 。
应用上述结论，不难判断图 3-31（a）及图 3-32（a）所示桁架中的零杆，如图 3-31（b）及图 3-32（b）中虚线所示。这样可使余下的计算工作大为简化。
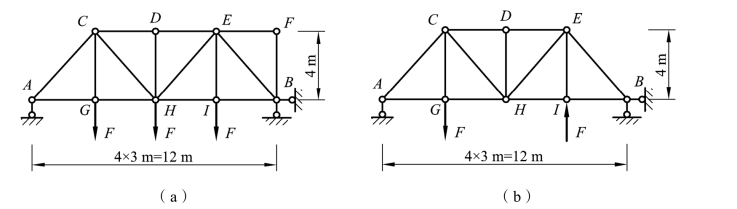
图3-30
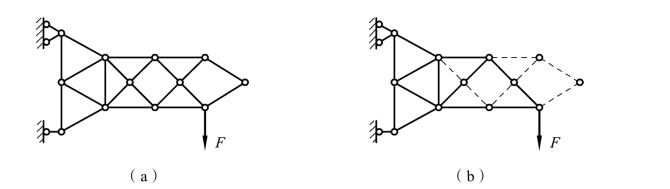
图3-31
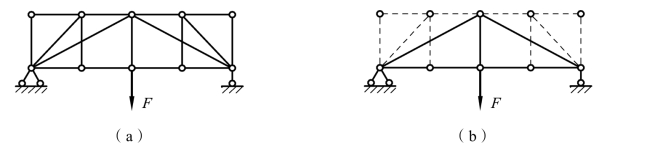
图3-32
若桁架处于对称或反对称的受力状态，在分析时只需计算半边桁架杆件的内力，另外半边杆件的内力可以根据对称或反对称的性质得到。此外，利用受力状态对称或反对称的特点也常可使计算进一步简化。例如，图 3-30（a）所示的桁架在撤去零杆EF 和BF 之后即属于对称受力状态，根据对称性要求，杆 HC 和 HE 轴力大小相等，且性质相同。因杆 HD是零杆，若结点H 无荷载则结点H 符合上述情况（4），它要求两斜杆的轴力性质相反。由于上述两种结论是矛盾的，因而可以判定FNHC=FNHE=0。如果结点H 上也作用有竖向荷载，则可以利用两斜杆内力相等的特点，由结点 H 的平衡条件∑Fy=0求出两杆的轴力FNHC=FNHE；如果将作用于结点I 上的荷载改为竖直向上，且大小不变［见图 3-30（b）］，则桁架处于反对称的受力状态，应有 FNDC=-FNDE，结合结点平衡的特殊情况（2），就可判定FNDC=FNDE= 0。
2.截面法
在桁架分析中，有时仅需或者是先需求出某一（或某些）指定杆件的内力，这时一般用截面法比较方便。截面法是用适当的截面，截取桁架中包含两个以上结点的部分为隔离体。此时，作用在隔离体上的各力通常构成平面一般力系，可以建立三个平衡方程。因此，若隔离体上的未知力不超过三个，则一般都可以利用这三个平衡方程解得。
在应用截面法时，为了避免联立求解，应注意选择合适的平衡方程，建立方程时，尽量把投影轴选在与未知力垂直的方向，矩心取在未知力的交点。
【例题3-8】 试用截面法计算图 3-33（a）所示桁架中a、b、c 三杆内力。
解：（1）求支座反力。
此为联合桁架，AB 为基本部分，BC 为附属部分，故可先从 BC 部分着手，取Ⅰ-Ⅰ截面右为隔离体［见图 3-33（c）］，由∑Fy=0，得
然后取整体为研究对象，求A、B 的反力：
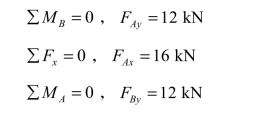
校核：∑Fy=FAy+FBy+FCy- 24 - 12 =0。
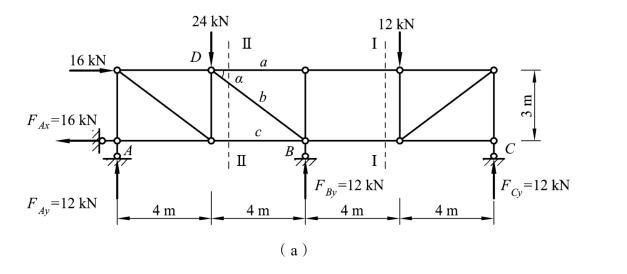
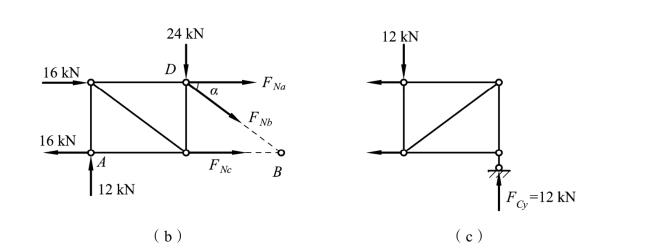
图3-33
（2）求内力，用截面Ⅱ-Ⅱ截取桁架的左边部分为隔离体［见图 3-33（b）］。
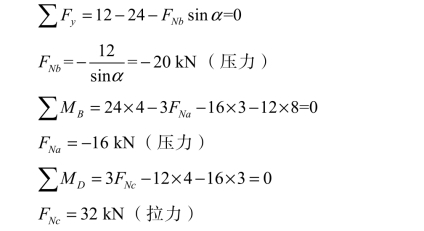
（3）校核：∑Fx=FNa+FNc+FNbcosα- 16 + 16 =0。
【例题3-9】 试求图 3-34（a）所示桁架中各指定杆的内力。
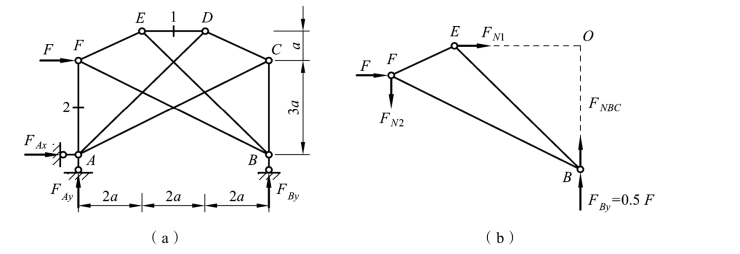
图3-34
解：这是一个联合桁架，它是由ACD 和BEF 两个简单桁架用BC, DE 和AF 三根链杆连接起来的。首先根据桁架整体的平衡条件，求得反力为
计算此类桁架的内力，通常需要将连接两个简单桁架的三根链杆切断，取其中一个简单桁架作为隔离体，如图 3-34（b）所示。被切断的三根链杆中，有两杆是竖直平行的，另一杆DE 则为水平。因此，由平衡条件
3.结点法和截面法的联合应用
结点法和截面法是计算桁架内力的两个基本方法。由于桁架的形式多种多样，因而在具体应用时，必须根据结构形式的不同灵活运用，并且有时往往需要两种方法同时应用才能解决问题。例如，图3-35 所示桁架的反力易于求得，根据结构的对称性，可先取A 和D 结点，但其余每一个结点上均有三根及以上的杆件轴力是未知的，所以无法单独从一个结点突破求解。分析其组成，桁架是由两个简单桁架根据两刚片规则组成的，现用截面法截断HI、GI、EJ 三根链杆，取Ⅰ-Ⅰ截面左为研究对象，以HI 和GI 两杆的汇交点为矩心可求得EJ 杆内力。同理，求出杆IH、IG 的内力，然后依次选取结点H、G、E、C、F 即可求出其余各杆件内力。
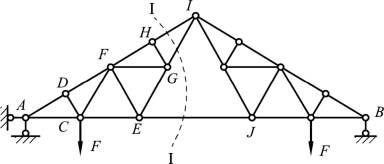
图3-35
用截面法求内力时尽量使所截杆件不超过三根，则可根据平衡条件求内力。然而在某些特殊情况下，只要所截杆件中除一根外其余各杆都相互平行或交于一点，则利用投影方程或力矩方程即可求出该杆内力。例如，对于图 3-36（a）所示桁架，为求杆a 的轴力，可取Ⅰ-Ⅰ截面所围的部分为隔离体，除杆a 外其余4 杆均交于A 点［见图 3-36（b）］，由∑MA=0可求得 FNa。
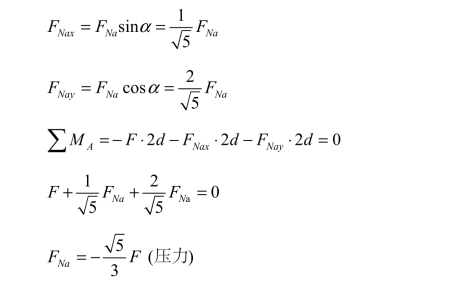
杆 a 的轴力求出后，再用结点法或截面法，其余各杆的内力也就不难求得。
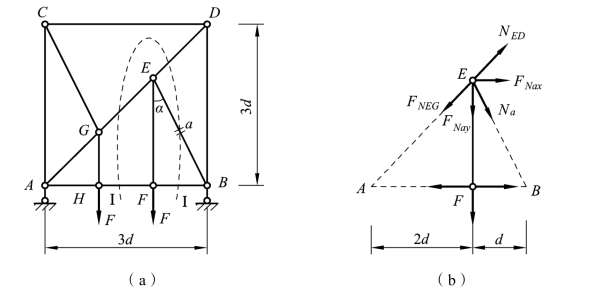
图3-36
又如，在图 3-37（a）所示的桁架中，为了求下弦杆 FG 的轴力，可作截面Ⅰ-Ⅰ，取隔离体如图 3-37（b）所示。这时，总共切断四根杆件，除下弦杆FG 外，其余各杆都相互平行。因此，取与各平行杆相垂直的方向为投影轴y,由力投影平衡方程得到
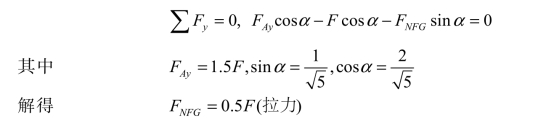
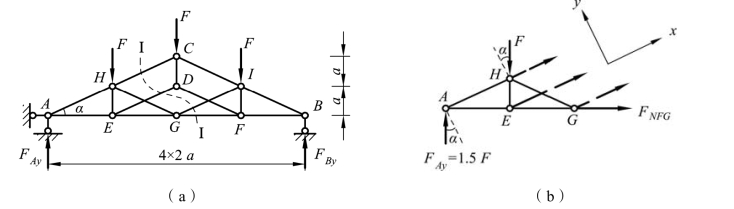
图3-37
上述桁架是对称的，在竖向荷载作用下不产生水平反力。因此，在对称竖向荷载作用下，桁架的反力和内力都应当对称。据此，从整体上看，杆件GH 和GI 的内力应当相等(等值同号)，即
然而，从局部来看，结点 G 为K 形结点，由结点G 的平衡条件，两者却应该相反（等值异号），即
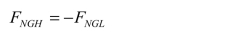
显而易见，要使以上两式都能得到满足，唯一的解答是
这样，去掉零杆，在结点H 或结点I 上，就只有三根杆件，其中一杆与荷载F 共线。因此，参照X 形特殊结点的结论，可得
上述各杆的内力求出后，再用结点法或截面法，其余各杆的内力也就不难求得。
有关结构力学的文章
- 详细阅读
-
静定平面刚架内力计算方法详细阅读
静定平面刚架的内力计算同梁一样，仍是用截面法截取隔离体，然后用平衡条件求解。根据荷载情况，将刚架分解成若干杆段，由平衡条件求出杆端内力。该杆上作用有一集中荷载，可以分为CE和EB两个无荷载区段，用截面法求出下列控制截面的弯矩：便可以绘制出该杆弯矩图。根据荷载和已经求出的反力，可以用截面法求出杆件各个控制截面的剪力和轴力，从而绘制出整个钢架的剪力图和轴力图，如图12-18、所示。......
2023-06-16
-
静定平面刚架内力计算方法(建筑力学第3版)详细阅读
静定平面刚架的内力包括弯矩、剪力与轴力。根据前述内力图绘制法逐杆绘制刚架的内力图，并进行校核。求支座反力时要根据支座的性质定出支座反力未知量的个数，然后假定反力方向，由平衡方程确定其数值。求图13-9所示刚架的支座反力。（二）刚架杆截面内力的计算1.刚架内力正负号的规定刚架的内力有弯矩、剪力和轴力。如杆端截面C1、C2的弯矩分别用MCA、MCD表示，剪力和轴力分别用QCA、QCD和NCA、NCD表示。......
2023-08-26
-
桁架内力计算方法及应用案例详细阅读
桁架的内力计算方法有节点法、截面法、联合法。桁架中某杆的轴力为零时，此杆称为零杆。图13-16试用节点法计算图13-17所示桁架的各杆内力。求图13-19所示桁架1、2、3杆的内力N1、N2、N3。如图13-20所示，欲求图中a杆的内力，如果只用节点法计算，无论取哪个节点为隔离体，都有三个以上的未知力，无法直接求解；如果只用截面法计算，也需要解联立方程。宜联合应用节点法和截面法，求所需反力和指定杆件内力。......
2023-08-26
-
结构力学：静定和超静定平面刚架的计算方法详细阅读
杆件轴线及荷载作用线均处在同一平面内的刚架，称为平面刚架。在工程中实际应用的刚架，多数是超静定的，静定刚架较少采用。图3-112.静定平面刚架计算静定刚架的内力通常有弯矩、剪力和轴力，其计算方法原则上与静定梁的计算相同。......
2023-08-30
-
1.8.3静定桁架计算方法：完整指南详细阅读
静定桁架一般采用节点法和截面法进行内力计算。 有一钢筋混凝土非预应力屋架，如图1.8-12所示。结构设计使用年限为50年。上弦杆的计算长度可取节间长度的两倍。基本组合为由可变荷载效应控制的组合。RAv=23.4 RAv=25.2 RAv=21 RAv=19.5答案：解答：荷载设计值：1.4×P2=8.4kN图1.8-12 图2.在恒荷载和活荷载的作用下，上弦杆件S1的内力设计值与下列（ ）项数值相接近。......
2023-08-28
-
支座移动时超静定结构内力的计算详细阅读
由于超静定结构有多余约束，因此，使结构产生变形的因素都将导致结构产生内力。这是超静定结构的重要特征之一，是静定结构所没有的。在实际工程中的结构除具有承受直接荷载的作用外，还受支座移动、温度改变、制造误差及材料的收缩膨胀等因素影响。下面将研究支座移动与温度改变时超静定结构的计算问题。由于支座移动在静定的基本结构中不引起内力，故只需将图乘以X1值即可。因此，由支座移动引起的杆件内力与杆的线刚度成正比。......
2023-08-26
-
3.2结构力学：多跨静定梁的内力计算详细阅读
图3-6多跨静定梁是由若干单跨静定梁相互用铰连接起来的，通常有两种基本形式。图3-82.多跨静定梁的内力计算从受力分析来看，由于基本部分直接与地基组成几何不变体系，因此它能独立承受荷载而维持平衡。......
2023-08-30
相关推荐