三铰拱为静定结构,其全部支座反力和内力都可由平衡条件确定。图12-22竖向荷载作用下的三铰拱内力计算1.支座反力的计算三铰拱有四个支座反力。即拱的竖向反力与相应简支梁的竖向反力相同。试计算图12-23所示三铰拱的内力,并绘制其内力图。图12-24三铰拱内力图弯矩图;剪力图;轴力图......
2023-06-16
现以图 3-20(a)所示的三铰拱为例说明其内力计算过程。该拱的两支座在同一水平线上,且只承受竖向荷载。
1.求支座反力
取拱整体为隔离体,由平衡方程∑MB=0,得

由∑MA=0,得
![]()
由∑Fx=0,得
![]()
再取左半个拱为隔离体,由平衡方程∑MC=0,得

与三铰拱同跨度同荷载的相应简支梁如图 3-20(b)所示,其支座反力为

同时,可以计算出相应简支梁C 截面上的弯矩为

比较以上诸式,可得三铰拱的支座反力与相应简支梁的支座反力之间的关系为

利用式(3-2),可以借助相应简支梁的支座反力和内力的计算结果来求三铰拱的支座反力。
由式(3-2)可以看出,只受竖向荷载作用的三铰拱,两固定铰支座的竖向反力与相应简支梁的竖向反力相同,水平反力Fx等于相应简支梁截面C 处的弯矩 与拱高f 的比值。当荷载与拱跨不变时,
与拱高f 的比值。当荷载与拱跨不变时,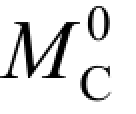 为定值,水平反力与拱高f 成反比。若f→0,则 Fx→∞,此时三个铰共线,成为瞬变体系。
为定值,水平反力与拱高f 成反比。若f→0,则 Fx→∞,此时三个铰共线,成为瞬变体系。
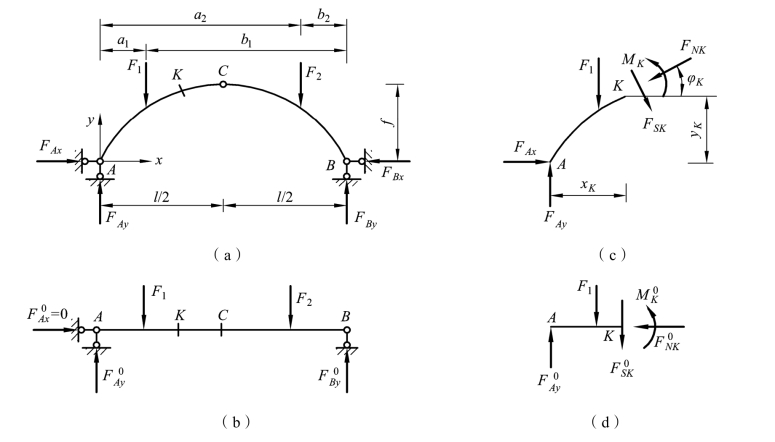
图3-20
2.求任一截面 K 上的内力
由于拱轴线为曲线,这使得三铰拱的内力计算较为复杂,但也可以借助其相应简支梁的内力计算结果,来求拱的任一截面K 上的内力。具体分析如下:
取三铰拱的K 截面以左部分为隔离体[见图 3-20(c)]。设 K 截面形心的坐标分别为 xK、yK,K 截面的法线与x 轴的夹角为φK。K 截面上的内力有弯矩 MK、剪力FSK和轴力 FNK。规定弯矩以使拱内侧纤维受拉为正,反之为负;剪力以使隔离体产生顺时针转动趋势时为正,反之为负;轴力以压力为正,拉力为负(在隔离体图上将内力均按正向画出)。利用平衡方程,可以求出拱的任意截面 K 上的内力为
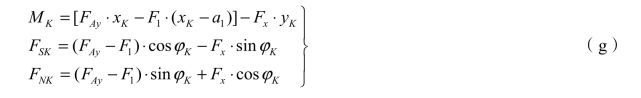
在相应简支梁上取如图 3-20(d)所示的隔离体,利用平衡方程,可以求出相应简支梁K截面上的内力为

利用式(h)与式(3-2),式(g)可写为

式(3-3)即为三铰拱任意截面K 上的内力计算公式。计算时要注意内力的正负号规定和夹角φK的取值,在左半拱时φK取正值,在右半拱时φK取负值。
由式(3-3)可以看出,由于水平支座反力Fx的存在,三铰拱任意截面K 上的弯矩和剪力均小于其相应简支梁的弯矩和剪力,并且存在着使截面受压的轴力。通常轴力较大,为主要内力。
3.绘制内力图
一般情况下,三铰拱的内力图均为曲线图形。为了简便起见,在绘制三铰拱的内力图时,通常沿跨长或沿拱轴线选取若干个截面,求出这些截面上的内力值。然后以拱轴线的水平投影为基线,在基线上把所求截面上的内力值按比例标出,用曲线相连,绘出内力图。
【例题3-8】 绘制图 3-21(a)所示三铰拱的内力图。已知拱轴线方程为:
![]()
解:(1)求支座反力。三铰拱的相应简支梁如图 3-21(b)所示。由式(3-2),并利用平衡方程,可得支座反力为
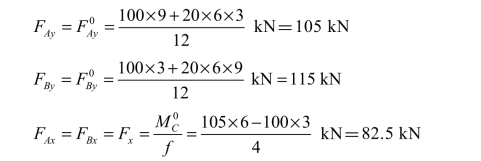
(2)求截面上的内力。为了绘制内力图,在三铰拱上沿拱跨每隔水平距离 1.5 m 取一个截面[见图 3-21(a)],分别计算这些截面上的内力值。现以截面 2 为例,说明内力的计算方法。
计算所需的有关数据为:

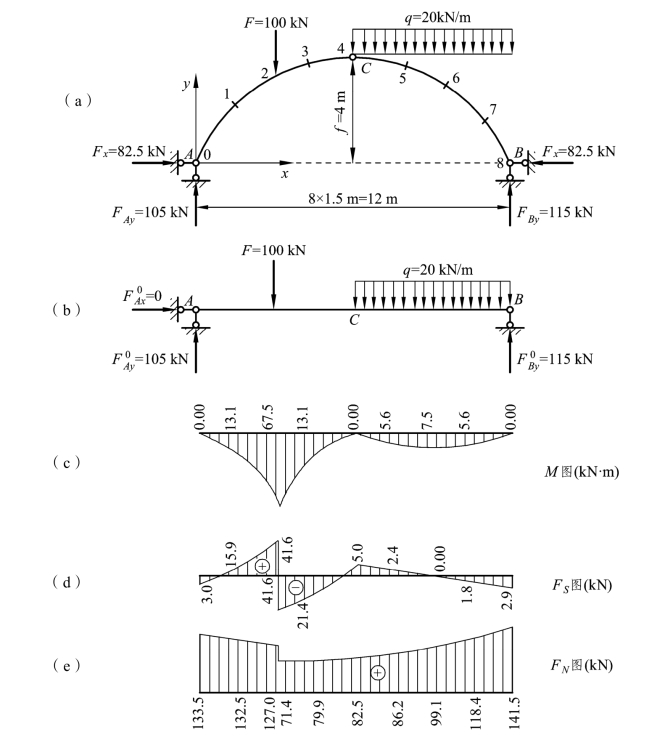
图3-21
由式(3-3),可得截面2 上的内力为:

必须指出,因为截面 2 处受集中荷载作用, 有突变,所以该处左、右两侧截面上的剪力和轴力不同,要分别加以计算。
有突变,所以该处左、右两侧截面上的剪力和轴力不同,要分别加以计算。
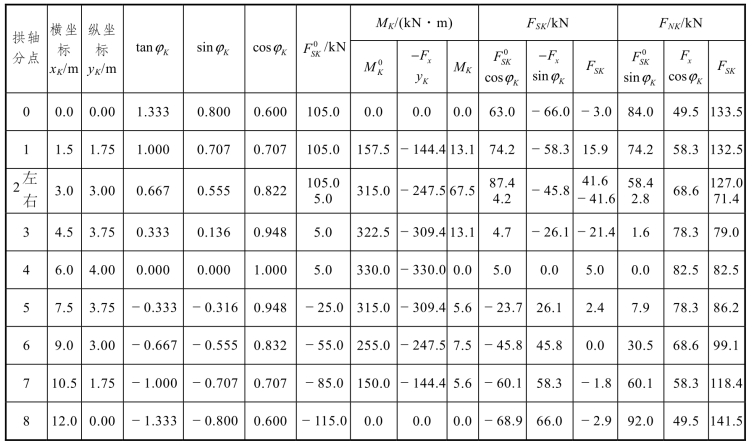
用同样的方法可计算其他各截面上的内力,其结果列于表3-2 中。
(3)绘制内力图。根据表 3-2 中的数值,用描点法逐一绘出弯矩图、剪力图和轴力图,分别如图 3-21(c)、(d)、(e)所示。
表3-2 三铰拱的内力计算
有关结构力学的文章

三铰拱为静定结构,其全部支座反力和内力都可由平衡条件确定。图12-22竖向荷载作用下的三铰拱内力计算1.支座反力的计算三铰拱有四个支座反力。即拱的竖向反力与相应简支梁的竖向反力相同。试计算图12-23所示三铰拱的内力,并绘制其内力图。图12-24三铰拱内力图弯矩图;剪力图;轴力图......
2023-06-16

三铰拱截面的内力有弯矩、剪力和轴力。上式表明,三铰拱的弯矩小于代梁的弯矩。由于拱轴坐标y及sinφ、cosφ都是x的非线性函数,所以,三铰拱的弯矩图、剪力图、轴力图都是曲线图形。计算时,通常将拱沿跨度分为若干等份,求出各分点处截面的内力值,然后连一曲线得到内力图。图13-33求三铰拱的支座反力。求三铰拱K截面的内力。......
2023-08-26

计算结果为正,表示ΔCx的方向与所设单位力的方向相同,即 ΔCx方向向右。 求图 5-17所示半圆弧三铰拱顶铰 C 两旁截面的相对转角。图5-17解:计算拱的位移,仅考虑弯矩对弯曲变形的影响,按公式计算。计算三铰拱受荷载及单位力偶作用时[见图 5-17、]的弯矩方程,应先求出支座反力,然后列出弯矩方程。此题由于三铰拱为对称结构,可只对拱的一半列出方程。......
2023-08-30

图3-6多跨静定梁是由若干单跨静定梁相互用铰连接起来的,通常有两种基本形式。图3-82.多跨静定梁的内力计算从受力分析来看,由于基本部分直接与地基组成几何不变体系,因此它能独立承受荷载而维持平衡。......
2023-08-30

由上可知,三铰拱任一截面的弯矩为当拱为合理拱轴时,各截面的弯矩应为零,即因此,合理拱轴的方程为式中,为相应简支梁的弯矩方程。不难看出,在竖向荷载作用下,三铰拱的合理拱轴的表达式与相应简支梁弯矩的表达式差一个比例常数H,即合理拱轴的纵坐标与相应简支梁弯矩图的纵坐标成比例。计算出图13-34所示三铰拱承受竖向均布荷载时的合理拱轴。显然,同一结构受到不同荷载的作用,就有不同的合理拱轴线方程。......
2023-08-26

求图 3-22所示三铰拱在竖向均布荷载q 作用下的合理拱轴。图3-22解:绘出拱的相应简支梁,如图 3-22所示,其弯矩方程为由式(3-3)可知,拱的水平推力为利用式(3-4),可求得合理拱轴的方程为由此可见,在满跨的竖向均布荷载作用下,对称三铰拱的合理拱轴为二次抛物线。需要指出,三铰拱的合理拱轴只是对一种给定荷载而言的,在不同的荷载作用下有不同的合理拱轴。......
2023-08-30

图3-452. 如图 3-46 所示,试不经过计算反力绘制出多跨静定梁的 M 图。已知三铰拱的拱轴线方程为:求水平推力。求铰 C 处的剪力和轴力。求集中力作用处轴线切线与水平轴的夹角。......
2023-08-30
相关推荐