静定平面刚架的内力计算同梁一样，仍是用截面法截取隔离体，然后用平衡条件求解。根据荷载情况，将刚架分解成若干杆段，由平衡条件求出杆端内力。该杆上作用有一集中荷载，可以分为CE和EB两个无荷载区段，用截面法求出下列控制截面的弯矩：便可以绘制出该杆弯矩图。根据荷载和已经求出的反力，可以用截面法求出杆件各个控制截面的剪力和轴力，从而绘制出整个钢架的剪力图和轴力图，如图12-18、所示。......
2023-06-16
结构力学：静定和超静定平面刚架的计算方法
【摘要】：杆件轴线及荷载作用线均处在同一平面内的刚架，称为平面刚架。在工程中实际应用的刚架，多数是超静定的，静定刚架较少采用。图3-112.静定平面刚架计算静定刚架的内力通常有弯矩、剪力和轴力，其计算方法原则上与静定梁的计算相同。
1.静定刚架的组成
刚架是由梁和柱等用刚结点连接而成的结构，其几何不变性主要依靠结点的刚性连接来维持，因而无须斜向杆件。这样，不但简化了结构形式，同时也更有利于建筑空间的利用。同时，由于有刚结点的存在，削弱了弯矩的峰值，使杆件的弯矩分布更趋于均匀。
杆件轴线及荷载作用线均处在同一平面内的刚架，称为平面刚架。在工程中实际应用的刚架，多数是超静定的，静定刚架较少采用。但静定刚架分析是超静定刚架计算的必要基础。
静定平面刚架常见的形式有悬臂刚架，如图 3-11（a）所示；简支刚架，如图 3-11（b）所示；三铰刚架，如图 3-11（c）所示等。
图3-11
2.静定平面刚架计算
静定刚架的内力通常有弯矩、剪力和轴力，其计算方法原则上与静定梁的计算相同。在静定刚架计算中，一般也需要对结构的组成情况进行分析，以便了解结构的具体特点及各部分之间的关系，应遵循先计算附属部分，后计算基本部分，即按几何组成相反的顺序，依次计算。
当刚架与基础按两刚片规则组成时，支座反力只有三个，容易求得；当刚架与基础按三刚片规则组成时（如三铰刚架），支座反力有四个，除考虑结构整体的三个平衡方程外，还需再取刚架的左半部（或右半部）为隔离体建立一个平衡方程，方可求出全部反力。反力求出后，即可逐杆段绘制内力图。
【例题3-4】 计算图 3-12（a）所示静定悬臂刚架的内力，并绘制内力图。
解：（1）求支座反力。
由整体平衡条件得：
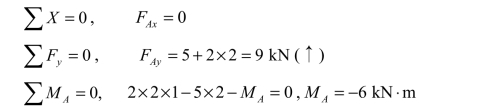
（2）计算杆端弯矩，绘制弯矩图。作弯矩图时，各杆逐一考虑，在刚架中，弯矩图绘于杆件受拉一侧。
BC 杆：
BC 为悬臂梁。B 端上侧边受拉，弯矩纵坐标绘于B 点上侧。C 端为自由端，弯矩等于零，将两点纵坐标连以直线，即得BC 杆的弯矩图。
BD 杆：
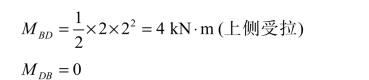
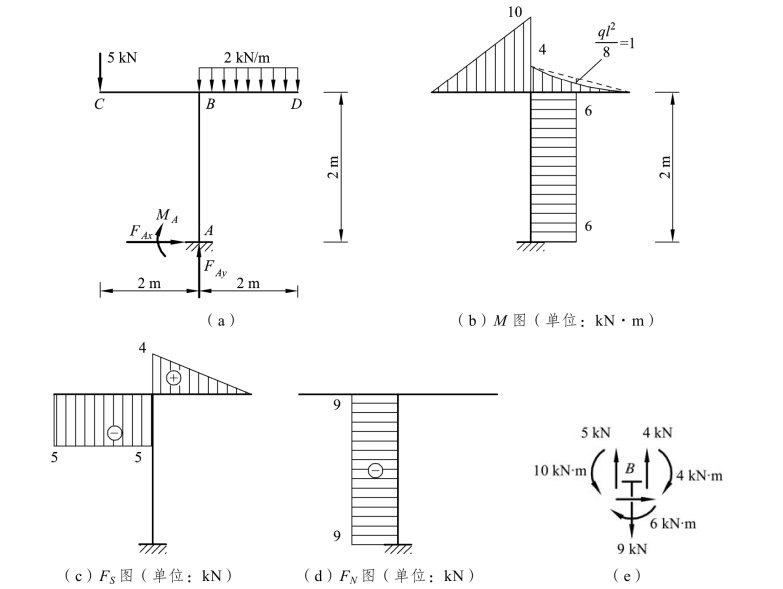
图3-12
BD 杆受均布荷载，B 端弯矩纵坐标绘于上侧。C 端弯矩为零，相应的纵坐标也为零，将两控制截面纵坐标连以虚线，并以此虚线作为基线，叠加相应简支梁在均布载荷作用下的弯矩图，即得到 BD 杆的弯矩图。由于荷载方向是向下的，故简支梁弯矩纵坐标应自虚线向下量取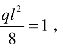
可见，即使是悬臂梁，也可看作是简支梁应用叠加原理绘制其弯矩图。
AB 杆：
AB 杆无荷载作用，两端截面弯矩相同，弯矩图为直线。
由以上可得整个刚架的弯矩图，如图 3-12（b）所示。
（3）计算杆端剪力，绘制剪力图。
根据杆端剪力值可作出刚架的剪力图，如图 3-12（c）所示。
（4）计算杆端轴力，绘制轴力图。
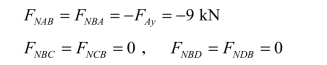
各杆轴力求出后，即可作出轴力图，如图 3-12（d）所示。
弯矩图绘制在杆件截面的受拉一侧，无须标明正、负号；绘制剪力图和轴力图时，正、负值应当绘于杆件的不同侧边，而且都必须注明正、负号。
（5）校核。
在刚架的计算中，除对内力的图形特征进行检查外，一般还需校核节点的平衡条件，本例取B 结点为隔离体，如图 3-12（e）所示，每个截面上的三种内力，取自三个内力图，其方向按如下方法定出：弯矩的箭头指向由杆件的受拉边指向受压边；剪力、轴力方向按前述规定。作用于该节点上的所有力，应当满足平面一般力系的三个平衡条件。显然，作用于节点 B 上所有力和力矩，是满足∑Fx=0、∑Fy=0及∑M =0的三个平衡条件的。
【例题3-5】 试作出图 3-13（a）所示刚架的内力图。
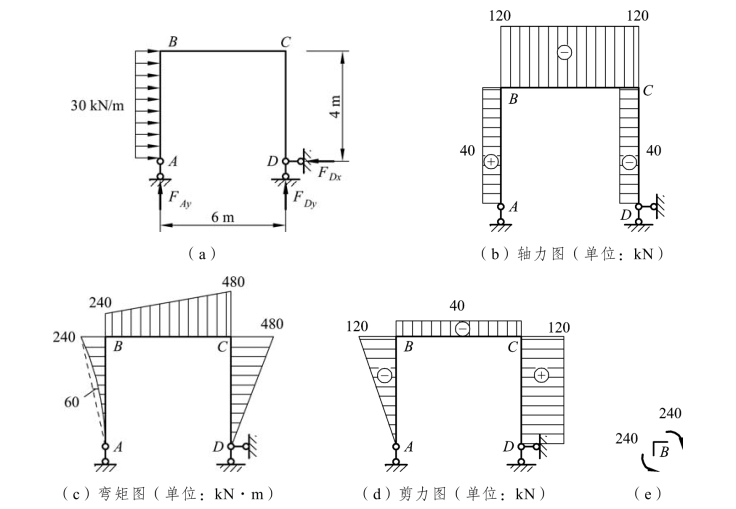
图3-13
解：（1）计算支座反力。
这是个简支刚架，考虑整体的平衡条件，由∑Fx=0可得
（2）绘制弯矩图。
作弯矩图时，逐杆绘制。
AB 杆：柱 AB 上受均布荷载作用，用叠加法绘制其弯矩图，先求杆端弯矩。
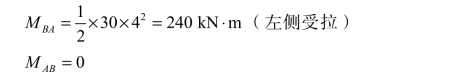
弯矩绘于 B 点左侧。将 A、B 两坐标的端点连以虚线，并以此虚线作为基线，叠加均布荷载所产生的简支梁的弯矩图，由于荷载方向是向右的，故简支梁弯矩纵坐标应自基线向右量取
DC 上无荷载，所以弯矩图为一直线。DC 两端截面弯矩分别为：
横梁 BC 上无荷载，弯矩图为一直线，两端弯矩数值为：
由此得出整个刚架的弯矩图，如图 3-13（c）所示。
需要指出，凡只有两杆交汇的刚结点，若结点上无外力偶作用，则两杆端弯矩必大小相等且同侧受拉（即同使刚架外侧或同使刚架内侧受拉）。本例刚架的结点B 或结点 C［见图3-13（e）］就属这种情况。
（3）绘制剪力图。
分别计算出各控制截面剪力。
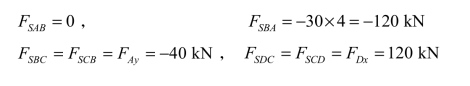
据此可作出剪力图，如图 3-13（d）所示。
同理，可绘出轴力图，如图 3-13（b）所示。
【例题3-6】 试作出图 3-14（a）所示三铰刚架的内力图。
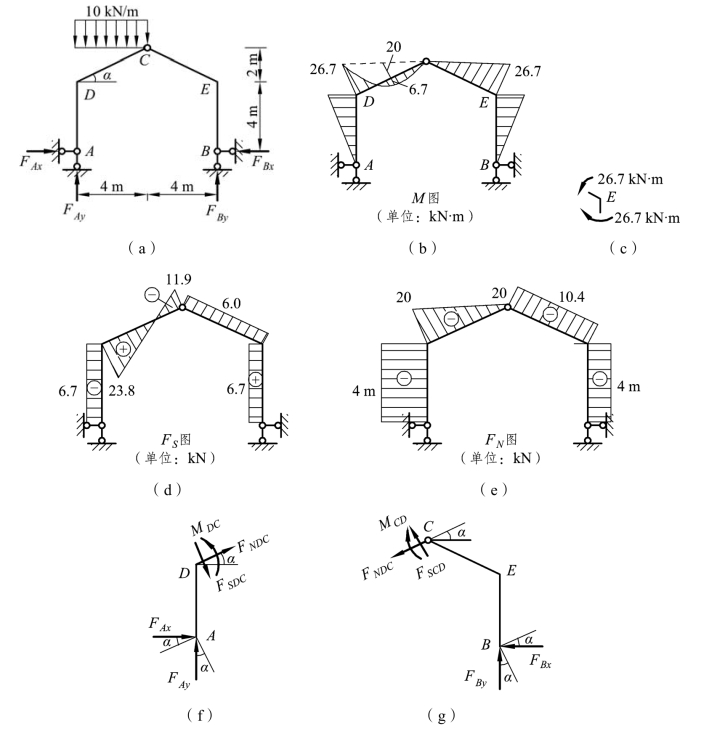
图3-14
解：（1）求反力。由刚架整体平衡∑MB=0，可得：
由∑Fy=0，得：
再取刚架右半部分为隔离体，由∑MC=0有
则得
（2）作弯矩图，以 DC 杆为例，先求出其两端弯矩：
连以直线（虚线），再叠加简支梁的弯矩图，杆中的弯矩为：
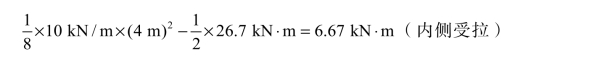
同理可求其余各杆端弯矩，绘出弯矩图，如图 3-14（b）所示。
（3）作剪力图和轴力图。以 DC 杆为例，求D 截面的剪力和轴力时，可取该截面以左部分 AD 为隔离体［见图 3-14（f）］，由截面法可得：
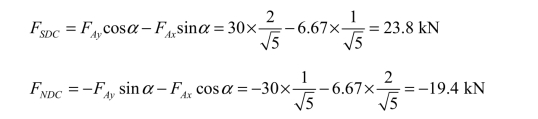
求 C 截面的剪力和轴力时，若取其右边部分CEB 为隔离体［见图3-14（g）］，则有
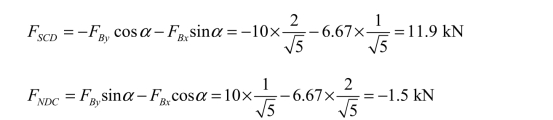
由此，即可绘出 CD 杆的剪力图和轴力图。其余各杆同理可求得，结果如图13-4（d）、（e）所示。
3.静定空间刚架
若刚架的各杆轴及所承受的荷载不在同一平面内，则称为空间刚架，无多余约束的几何不变的空间刚架，称为静定空间刚架。确定一个自身为几何不变的空间刚架在空间的位置，需要六根不相交在同一直线上的支杆与基础连接，体系才能成为不变，如图 3-15（a）所示。图中的刚架，虽然各杆轴线都在 Oxy 平面内，但荷载不在此平面内，故亦属于空间刚架，也称为平面刚架承受空间荷载。
空间刚架的杆件横截面上一般有六个内力分量［见图 3-15（b）］，即轴力NF （沿杆轴线方向），剪力 FSy和 FSz(分别沿横截面的两个形心主轴方向），弯矩Mx和My(分别绕两形心主轴旋转的力偶），以及扭矩Mz(绕杆轴线旋转的力偶）。为了清楚起见，力偶都按右手螺旋法则用双箭头矢量表示。
各内力分量的正、负号以图 3-15（b）中所设的方向为正，反之为负。通常以杆轴为 x轴并以截面的外法线为x 轴的正方向；以截面的两个主轴为y 轴和z 轴，按右手螺旋法则定出y 轴和z 轴的正方向。
图3-15
计算静定空间刚架内力的基本方法，仍是截面法。从静定空间刚架中截取不超过六个未知内力分量的隔离体，由空间一般力系的六个平衡条件，可求得截面上的六个内力分量。作内力图时，可逐杆建立各内力方程，再按各内力方程作图。或首先分段求作各控制截面的内力，再根据作用于杆件的荷载情况作出各杆的内力图。作空间刚架的内力图时，弯矩纵标仍画在杆件受拉纤维一侧，弯矩图上不标明正负号；轴力图、剪力图和扭矩图可画在杆件的任一侧，但需标明正、负号。
【例题 3-7】 试求图 3-16（a）所示的空间刚架的支座反力，并作内力图。水平杆 CD平行于坐标轴 z，水平荷载垂直于 CD 杆作用。
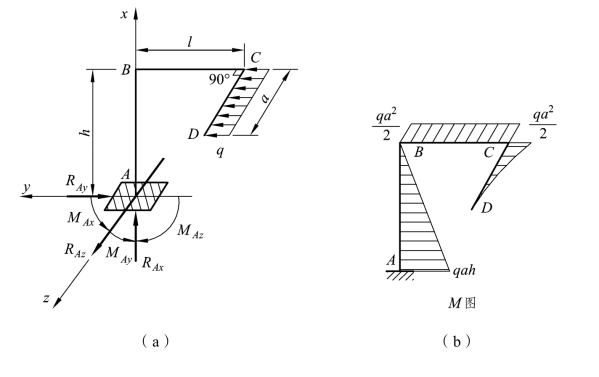
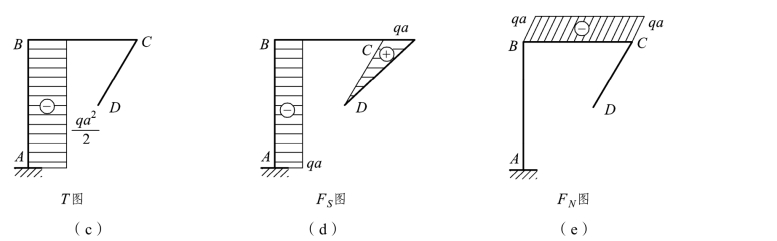
图3-16
解：设各支座反力的方向如图 3-16（a）所示，则由刚架的平衡条件可得：
由于荷载与刚架的 BCD 部分处在同一平面内，故该部分属于平面受力状态。柱 AB 除了在 xy 平面内承受弯矩外，并承受沿杆轴为常量的扭矩TAx=-MAx=-qa2/2。此刚架的 M 图、T 图、FS图和FN图，分别如图 3-40（b）、（c）、（d）、（e）所示。
有关结构力学的文章
- 详细阅读
-
静定平面刚架内力计算方法(建筑力学第3版)详细阅读
静定平面刚架的内力包括弯矩、剪力与轴力。根据前述内力图绘制法逐杆绘制刚架的内力图，并进行校核。求支座反力时要根据支座的性质定出支座反力未知量的个数，然后假定反力方向，由平衡方程确定其数值。求图13-9所示刚架的支座反力。（二）刚架杆截面内力的计算1.刚架内力正负号的规定刚架的内力有弯矩、剪力和轴力。如杆端截面C1、C2的弯矩分别用MCA、MCD表示，剪力和轴力分别用QCA、QCD和NCA、NCD表示。......
2023-08-26
-
结构力学：超静定次数确定详细阅读
超静定结构中的多余约束数目称为超静定次数。用力法计算超静定结构时，通常是取静定结构作为基本结构，这就需要把超静定结构中的多余约束解除，使其变为静定结构。将原结构变成静定结构所需去除的多余约束数目即为超静定次数，也就是力法基本未知量的数目。图6-3图6-4图6-5对于某一个超静定结构，去除掉多余约束的方式有很多种，但必须注意以下两点：去掉的约束必须是多余约束。因此，原结构共有四个多余约束，是四次超静定结构。......
2023-08-30
-
特性,超静定结构-结构力学详细阅读
超静定结构与静定结构对比，具有以下一些重要特性。了解这些特性，有助于加深对超静定结构的认识，并更好地应用。超静定结构的这一特性，在一定条件下会带来不利影响，例如连续梁可能由于地基不均匀沉陷而产生过大的附加内力。但超静定结构的内力单由平衡条件则无法全部确定，还必须考虑变形条件才能确定其解答，因此其内力数值与材料性质和截面尺寸有关。因此，从军事及抗震方面来看，超静定结构具有较强的防御能力。......
2023-08-30
-
静定平面桁架内力的计算方法详细阅读
平面汇交力系可以建立两个独立的平衡方程，解算两个未知量。继续取8、6、7等结点为隔离体，可求得桁架右半边各杆的内力。图12-30桁架轴力示意在桁架内力计算时，往往会遇到内力为零的杆件，这种杆件称为零杆。计算桁架的内力宜从几何分析入手，以便选择适当的计算方法，灵活地选取隔离体和平衡方程。除结点法外，计算桁架内力的另一基本方法是截面法。截面法适用于联合桁架的计算以及简单桁架中求少数指定杆件内力的情况。......
2023-06-16
-
超静定结构的概念-结构力学书详细阅读
在前面各章中，已经详细地讨论了静定结构的计算问题，静定结构的全部反力和内力可由静力平衡条件确定。超静定结构的应用范围很广，图6-1 所示为一些工程中常见的超静定结构类型。图6-1常见的超静定结构从本章开始，我们将讨论超静定结构的计算问题。按照线弹性的计算理论，超静定结构的计算方法主要有以下两种：力法。力法和位移法是超静定结构计算的基本方法。......
2023-08-30
-
用位移法计算连续梁与超静定刚架详细阅读
位移法计算连续梁及超静定刚架一般步骤如下：确定基本未知量和基本结构。用位移法计算时，只有节点转角基本未知量，故仅需建立刚节点处的力矩平衡方程，即可求解出全部未知量，进而计算杆端弯矩，绘制出内力图。此连续梁只有一个刚节点B的转角位移θB，如图15-32所示。列各杆杆端弯矩计算式。用位移法计算图15-34所示的超静定刚架，并作出弯矩图。......
2023-08-26
-
超静定结构的位移计算方法详细阅读
变形体的虚功原理及其相应的单位力法并不仅限于求解静定结构的位移，同样也适用于求解超静定结构的位移，问题是如何使计算得到简化。这两个弯矩图都是经超静定结构的力法计算所得。若按图 6-39和图 6-39进行图乘计算，得结果与前相同，说明方法正确，即计算超静定结构的位移可采用去除多余约束后的静定结构建立虚拟力状态，把问题转化为静定结构的位移计算，这将使计算工作大为简化。......
2023-08-30
相关推荐