根据力法的基本原理，力法计算超静定结构的方法和步骤可归纳如下：确定超静定次数，并选取适当的基本结构。应当注意的是，在选取基本结构时，若解除多余约束的方案不同，则将会得到不同形式的基本结构，虽然其力法典型方程的基本形式相同，超静定结构的求解步骤和最终结果亦相同，但计算工作量可能会有很大的差异。以下分别举例说明用力法计算各类超静定结构的具体计算方法。......
2023-08-30
结构力学：轴力和弯矩快速了解
【摘要】：截面内力沿杆轴切线方向的分力称为轴力。截面内力对截面形心的力矩称为弯矩。
1.内力的种类及其符号规定
平面结构在任意荷载作用下，杆件截面上的内力一般有三个分量：轴力FN、剪力FS和弯矩M，如图3-1 所示。
截面内力沿杆轴切线方向的分力称为轴力。轴力以拉力为正，压力为负。
截面内力沿杆轴法线方向的分力称为剪力。剪力对截取的隔离体邻近截面顺时针旋转者为正，反之为负。
截面内力对截面形心的力矩称为弯矩。弯矩在水平杆中，当弯矩使杆件下部纤维受拉时，弯矩为正，反之为负。
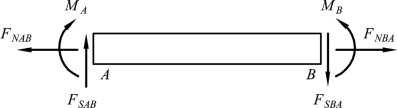
图3-1
为明确地表示杆件上不同截面的内力，一般在内力符号后面引用两个脚标：第一个表示内力所属截面，第二个表示该截面所属杆件的另一端。
2.截面法求内力及内力图
静定结构的全部反力和内力都可以根据静力平衡条件求得，计算截面内力的基本方法是截面法。所谓截面法，就是用假想的截面将杆件沿欲求内力的截面截开，取截面的任意一侧为隔离体（受力简单部分），利用隔离体的平衡条件一般可列出三个平衡方程，从而求得该截面的三个内力分量。
根据隔离体的平衡条件可得：
轴力等于截面任一侧隔离体上所有外力沿杆轴切线方向投影的代数和。
剪力等于截面任一侧隔离体上所有外力沿杆轴法线方向投影的代数和。
弯矩等于截面任一侧隔离体上所有外力对截面形心力矩的代数和。
或用公式来表示：
式中各力的投影及力矩符号请读者自行确定。
表示结构上杆件各截面内力数值的图形称为内力图，通常是用平行于杆轴线的坐标表示截面的位置（此坐标轴通常又称为基线），而用垂直于杆轴线的纵坐标表示内力的数值所绘出的。在结构力学中，要求弯矩绘在杆件纤维受拉的一侧，无须在图上标明正负号。剪力图和轴力图则将正值的纵坐标绘在基线的上方，同时标明正负号。
3.荷载与内力的微分关系及内力图的特征
截面法可以很方便地求出指定截面的内力，但如要绘制内力图，还需要应用荷载与内力之间的微分关系，掌握内力图的特点，才能迅速绘制内力图或者校核内力图的正确性。
如图 3-2（a）所示为一静定简支梁，梁上作用有水平分布荷载 qx及竖向分布荷载 qy，集中力F，集中力矩m。取出梁上一个微段如图 3-2（b）所示。
由平衡方程：∑Fx=0，∑Fy=0，∑M =0，可得直杆内力与荷载之间的微分关系：
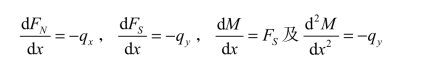
图3-2
应用直杆内力与荷载的微分关系，可确定控制截面之间内力图形的正确形状，如表 3-1所示，掌握内力图的形状特征有助于正确并快速地绘制出内力图。
表3-1 剪力图与弯矩图形状特征
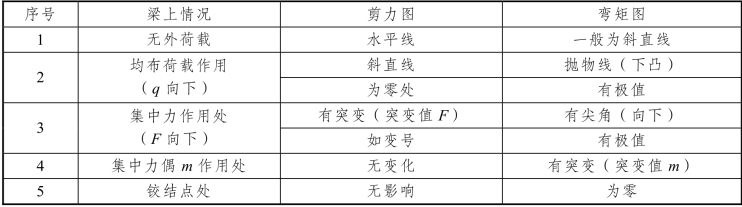
4.绘制直杆弯矩图的区段叠加法
叠加原理是力学分析中的一个基本理论，可表述为：结构中一组荷载作用所产生的效应（反力、内力和位移等）等于每一个荷载单独作用所产生的效应的总和。这意味着这些荷载的效应与荷载的关系必须是线性的，下面介绍利用叠加原理绘制直杆段弯矩图的方法。
我们先来用叠加法绘制简支梁的弯矩图。如图 3-3（a）所示简支梁同时承受集中力和两端力偶的作用，可先分别绘出两端力偶 MA、MB作用下和荷载 F 作用下的弯矩图
图、M0图，如图 3-3（b）、（c）所示。然后将其纵坐标叠加，即得所求弯矩图 M 图［见图 3-3（d）］，实际作图时，不必作出图 3-3（b）、（c）而可直接作出图 3-3（d）。具体做法是：先将两端弯矩MA、MB的纵坐标绘出并连以直线（虚线），然后以此直线为基线叠加简支梁在荷载F 作用下的弯矩图。需要注意的是，这里所说的弯矩图的叠加，是纵坐标值的叠加，而不是图形的简单拼凑，因此，图 3-3（d）中的纵坐标 Fab/l 是沿垂直于杆轴线方向从 MA、MB连线开始量取而不是垂直于 MA、MB连线方向。这样，最后的图线与最初基线（杆轴线，是量取纵坐标的起点）之间所包含的图形即为叠加后所得的弯矩图。
上述叠加法对直杆的任何区段都是适用的。如图 3-4（a）所示梁中某一区段AB，取出该梁段为隔离体［见图 3-4（b）］，除荷载 q 外，两端还有弯矩 MA、MB和剪力 FSAB、FSBA作用。如果把它与一个长度相等承受同样荷载q 并在两端还有力偶 MA、MB作用的简支梁［见图 3-4（c）］相比，在二者中分别用平衡条件求其剪力 FSAB、FSBA及支座反力FA、FB，则可知FSAB＝FA、FSBA＝－FB，可见，它们所受的外力完全相同，因而二者具有相同的内力及内力图。于是，这段梁的弯矩图就可以这样来绘制：先将其两端弯矩MA、MB求出并连以直线（虚线），然后在此直线上再叠加相应简支梁在荷载 q 作用下的弯矩图，即得AB 段弯矩图［见图 3-4（d）］，这种方法可称为区段叠加法。
应用区段叠加法绘制弯矩图时，其步骤可归纳为：
（1）求控制截面弯矩，以外荷载的不连续点，如集中力及集中力偶作用点、均布荷载的起（止）点、支座及结点等为控制截面，求出其弯矩值。
（2）分段绘制弯矩图，将控制截面弯矩值在基线上用纵坐标绘出，当控制截面间无荷载作用时，用直线连接两控制面的弯矩值，即得该段弯矩图；当区段内有荷载作用时，先用虚线连接两控制面的弯矩值，然后以此为基线，再叠加相应荷载作用在这段简支梁的弯矩图，从而绘制出最后的弯矩图。弯矩图的凸向与荷载指向一致。
所谓区段叠加法，就是利用相应简支梁的弯矩图的叠加来作直杆某一区段弯矩图的方法。
图3-3
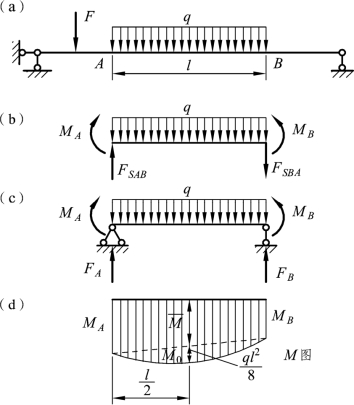
图3-4
【例题 3-1】 试作图 3-5（a）所示梁的弯矩图和剪力图。
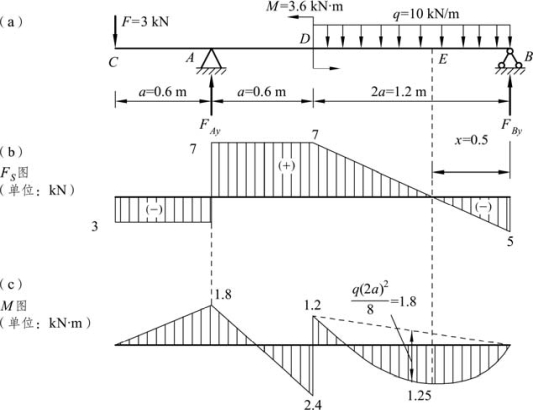
图3-5
解：（1）求支座反力。
以梁整体为隔离体，由平衡方程∑MB=0，得
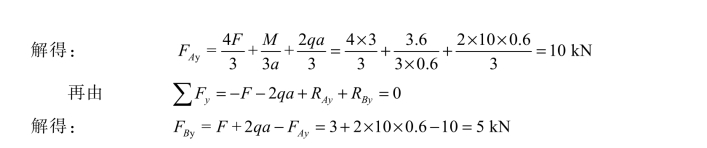
（2）绘制剪力图。
绘制剪力图时，先用截面法计算出各控制截面的剪力值。
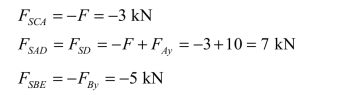
计算出各控制截面的剪力值即可作出剪力图，如图 3-5（b）所示。
剪力最大值： Fmax=7 kN 。
（3）作弯矩图。
绘制弯矩图时，先用截面法计算出各控制截面的弯矩值。
计算出各控制截面的弯矩值便可绘制出弯矩图，以梁轴线为横轴（基线），将各弯矩值MC、MA、MDA标于坐标上，分别以直线连接，得 CA、AD 段的弯矩图；将 MDB、MB、ME各值标于坐标上，分别连以直线（虚线），再叠加均布荷载作用于简支梁的弯矩图，即得 DB段的弯矩图，全梁的弯矩图如图3-5（c）所示。由图可见 D 处左侧截面上的弯矩最大，为：Mmax=2.4 kN · m 。
有关结构力学的文章
- 详细阅读
-
合理拱轴概念的作用,结构力学详细阅读
求图 3-22所示三铰拱在竖向均布荷载q 作用下的合理拱轴。图3-22解：绘出拱的相应简支梁，如图 3-22所示，其弯矩方程为由式（3-3）可知，拱的水平推力为利用式（3-4），可求得合理拱轴的方程为由此可见，在满跨的竖向均布荷载作用下，对称三铰拱的合理拱轴为二次抛物线。需要指出，三铰拱的合理拱轴只是对一种给定荷载而言的，在不同的荷载作用下有不同的合理拱轴。......
2023-08-30
-
简支梁的绝对最大弯矩和内力包络图-《结构力学详细阅读
据此可以判断，在荷载组中部的几个集中荷载作用的截面，发生绝对最大弯矩的可能性最大。经验表明，在通常情况下产生简支梁绝对最大弯矩时的临界荷载 FK就是使跨中截面产生最大弯矩时的临界荷载。试求简支梁的绝对最大弯矩，并与跨中截面 C 的最大弯矩相比较。包络图分为弯矩包络图和剪力包络图。......
2023-08-30
-
建筑CAD：快速创建标高和轴网详细阅读
图9-4创建标高2.创建F3、F4、F5、F6选择“建筑”→基准“标高”→“”→“阵列”命令，单击“F2”标高线并将回车键，得到图9-5。注意：注：如果层数过多，方便起见，可以采用F1、F2、F3等作为标高名称。在“项目浏览器”中双击“立面”项下的“南”立面进入南立面视图，使用前述编辑标高和轴网的方法，调整标头位置、添加弯头。此时，各层视图均出现轴。......
2023-09-19
-
虚功原理和单位力法解析-结构力学详细阅读
变形体系的虚功原理可表述为：变形体系处于平衡的必要和充分条件是，对于符合变形体系约束条件的任意微小的连续虚位移，变形体系上所有外力所做的虚功总和外W ，等于变形体系各微段截面上的内力在其虚变形上所做的虚功总和U变。虚功原理更一般地表示为：由以上可见，虚功原理需要涉及两个状态，取一个状态的外力和内力，取另一个状态的位移和变形。如果位移是虚设的，则称为虚位移原理；如果外力是虚设的，则称为虚力原理。......
2023-08-30
- 详细阅读
-
单结点结构的弯矩分配法-结构力学技巧详细阅读
以上两种情况叠加即为结构的实际受力状态，将第一步中各杆端的固端弯矩分别和第二步中的各杆端分配弯矩以及传递弯矩叠加，可得该结点各杆的近端或远端的最后弯矩。......
2023-08-30
-
轴和轴承：用途和分类详细阅读
(一)轴的用途及分类轴是组成机器的主要零件之一。在高速、高精度、重载、结构上要求剖分等场合下，滑动轴承就显示出它的优异性能，对于在低速但有冲击的条件下工作的机器，也采用滑动轴承。图3-14所示为一整体式滑动轴承，它由轴承座和整体轴瓦等组成。轴承合金又称巴氏合金。铅锑轴承合金的各种性能与锡锑轴承合金接近，但这种材料较脆，不宜承受较大的冲击载荷，一般用于中速、中载的轴承。......
2023-06-16
相关推荐