利用组成几何不变体系的基本规则,可以组成各种各样的几何不变体系,也可以利用这些规则对已有的体系进行几何组成分析。下面将通过具体的例子来说明平面体系的几何组成分析。两刚片由铰 C 和杆 IJ 连接,根据规则 2 可知,体系为几何不变体,且无多余约束,作为一个大刚片。 试对图 2-16所示体系做几何组成分析。如果铰B 和虚铰O1、O2不在同一条直线上,则此体系为无多余约束的几何不变体系;如果此三铰在同一条直线上,则为瞬变体系。......
2023-08-30
以上主要按机械运动及几何学的观点,论述了各种体系的几何特征。本节将按静力平衡的观点,来讨论几种体系的静力特性。
1.静定结构的静力特征
静定结构,几何组成上是没有多余约束的几何不变体系,如图2-17(a)所示的梁,它与基础用不交于一点且不平行的三根链杆(支杆)相连,符合组成规则 2,故为无多余约束的几何不变体系。有三个未知反力,可由平面一般力系三个平衡方程∑Fx=0、∑Fy=0、∑M =0求得。从而其全部的内力可由平衡条件确定,且解答是唯一的。当荷载为零时,体系的反力和内力也等于零。
2.超静定结构的静力特性
超静定结构,几何组成上是具有多余约束的几何不变体系,如果上述梁有四根支杆与基础相连,如图 2-17(b)所示,则它就变成具有一个多余约束的几何不变体系。考虑该梁的整体平衡条件,仍只能建立三个独立的平衡方程。因此,若要求出这些反力,还必须根据梁的实际变形情况(例如A 或B 点的竖向位移为零),建立一个变形协调方程。
当荷载为零时,体系也可以有非零的反力和内力。这种没有荷载,而体系可以有非零反力和内力的情况,称作初内力或自内力状态。体系可以产生和存在初内力或自内力,这是超静定结构极为重要的一个静力特性。
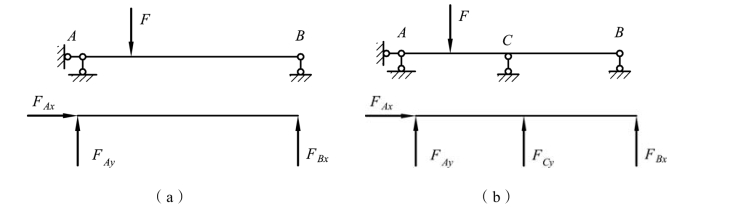
图2-17
3.瞬变体系的静力特性
有关瞬变体系的几何特征,已在第三节中做了比较详细的介绍,这里我们将讨论它的静力特性。
现分析图 2-18(a)中三铰共线的情况。由图可知,当刚片Ⅰ、Ⅱ分别绕A、B 转动时,在 C 处有一公切线。这说明刚片Ⅰ、Ⅱ都允许 C 点沿AC、BC 铅垂方向移动。但一旦发生微小移动后,A、B、C 三铰就不在同一直线上,C 点就不能再动了。这种只在某一瞬间能发生微小移动,过后就不再动的体系,称为瞬变体系。既然瞬变体系只是瞬时可动,随后就变为几何不变的了,那么工程结构可否采用呢?分析一下图 2-18(a)所示体系的内力,就可得知。取结点 C 为隔离体,如图 2-18(b)所示,则
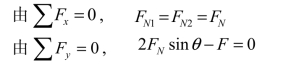
则
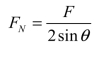
当F ≠0 时,θ 越小,FN就越大;当θ =0 也就是三铰共线时,NF =∞,这说明瞬变体系即使在很小的荷载作用下,也会产生无穷大的内力而导致体系的破坏,故瞬变体系不能用于工程结构。
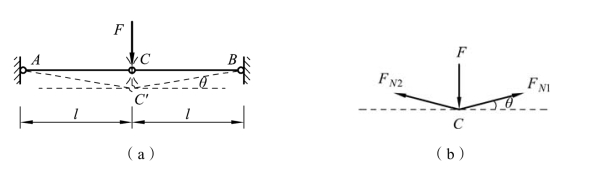
图2-18
有关结构力学的文章

利用组成几何不变体系的基本规则,可以组成各种各样的几何不变体系,也可以利用这些规则对已有的体系进行几何组成分析。下面将通过具体的例子来说明平面体系的几何组成分析。两刚片由铰 C 和杆 IJ 连接,根据规则 2 可知,体系为几何不变体,且无多余约束,作为一个大刚片。 试对图 2-16所示体系做几何组成分析。如果铰B 和虚铰O1、O2不在同一条直线上,则此体系为无多余约束的几何不变体系;如果此三铰在同一条直线上,则为瞬变体系。......
2023-08-30

当P 点偏离原位置后,2 个杆与刚片构成三角形,成为几何不变体系。将这样的在原位置上可以发生微小运动,运动后成为几何不变的体系称为瞬变体系。由此可得:规则 1:1 个点和1 个刚片用2 根不在同一直线上的链杆相连,构成内部几何不变且无多余约束的体系。二元片的构造不改变原体系的自由度。......
2023-08-30

图11-15二元体利用二元体规则可以使某些体系的几何组成分析得到简化,也可以直接对某些体系进行几何组成分析。由二元体规则可知,此体系是几何不变体系,并且没有多余约束。然后,将其视为一个更大刚片,它与BC杆再用铰B和不通过该铰的链杆2相连,又组成几何不变体系,且没有多余约束。......
2023-06-16

如果我们把面积与轨迹联系起来,分析一些与面积有关的轨迹问题,就能较丰富地体现集合概念,使集合思想更多地渗入平面几何之中。[例6.1.1]设A、B、C、D4点在一条直线上,试求平面上满足条件△PAB=△PCD的点P的轨迹。[例6.1.5]若ABCD是平行四边形,a是给定的正数,求平面上满足条件△PAB+△PCD=a的点P的轨迹。解:分三种情形:若ABCD面积大于2a,所求轨迹是空集。......
2023-10-17

根据组成几何不变体系的基本规则对体系进行几何组成分析。作几何组成分析时,为了使分析过程简化,应注意以下两点:可将体系中的几何不变部分当作一个刚片来处理。则连接三刚片的三个铰A、B、O不在一直线上,符合三刚片规则,故体系为几何不变且无多余约束。CDE和基础视为两刚片,两刚片用三根链杆1、链杆2、链杆3相连,此三根链杆汇交于同一点,所以体系为几何可变体系。......
2023-08-26

由基本规则分析可知,平面体系几何组成规则本身是非常简单容易理解的,都是三角形法则。那么,如何灵活利用平面结构体系几何组成基本规则,对所有纷繁复杂的平面体系进行几何组成分析,关键在于要掌握分析技巧。(二)合理选择和扩大平面杆件体系中的刚片对简化后杆件体系进行几何组成分析时,刚片的选择尤为重要,一般应遵循以下原则:首先要看简化后体系是否还存在地基,若存在直接将地基看成一个刚片,依次根据规则扩大刚片。......
2023-08-26

氧原子分别与两个氢原子各形成一对共用电子对,从而结合成稳定的分子。但由于共用电子对明显靠近氧原子一侧,导致氧原子附近形成负电荷中心,氢原子附近形成正电荷中心,这种现象称为水分子的极性,几乎水的所有特性都与水分子的极性密切相关。由于水分子具有极性,所以水分子中的氢原子能够与附近水分子中的氧原子发生正负电荷相吸现象,从而在临近水分子之间形成一种相互联结的作用力,称为氢键。......
2023-06-30
相关推荐