由基本规则分析可知，平面体系几何组成规则本身是非常简单容易理解的，都是三角形法则。那么，如何灵活利用平面结构体系几何组成基本规则，对所有纷繁复杂的平面体系进行几何组成分析，关键在于要掌握分析技巧。（二）合理选择和扩大平面杆件体系中的刚片对简化后杆件体系进行几何组成分析时，刚片的选择尤为重要，一般应遵循以下原则：首先要看简化后体系是否还存在地基，若存在直接将地基看成一个刚片，依次根据规则扩大刚片。......
2025-09-30
结构力学：平面体系几何组成分析实例
【摘要】：利用组成几何不变体系的基本规则，可以组成各种各样的几何不变体系，也可以利用这些规则对已有的体系进行几何组成分析。下面将通过具体的例子来说明平面体系的几何组成分析。两刚片由铰 C 和杆 IJ 连接，根据规则 2 可知，体系为几何不变体，且无多余约束，作为一个大刚片。 试对图 2-16所示体系做几何组成分析。如果铰B 和虚铰O1、O2不在同一条直线上，则此体系为无多余约束的几何不变体系；如果此三铰在同一条直线上，则为瞬变体系。
利用组成几何不变体系的基本规则，可以组成各种各样的几何不变体系，也可以利用这些规则对已有的体系进行几何组成分析。下面将通过具体的例子来说明平面体系的几何组成分析。
【例题 2-3】 试对图 2-12（a）所示体系做几何组成分析。
解：自身内部为几何不变的一个平面体系，它仅需要3 根支杆（链杆）与基础相连，就可保持几何不变了。可是本例却有4 根支杆，说明体系外部具有一个多余约束，对于此类体系，其内部有可能是缺少约束的，依靠增加外部约束来弥补体系内部约束的不足。因此，在分析此类体系的几何组成时，应当连同基础一起考虑。在该体系中，曲杆 AEC 和BFD 上各有三个连接点，一般不宜当作链杆，而应当分别看作刚片。两端铰接的直杆CD 和EF 都是链杆。支座A 和B 都是铰支座，可分别当作铰来看待。先假设基础为刚片I，把与基础相连的刚片AEC 和BFD 分别看作刚片Ⅱ和Ⅲ。最后，再看刚片Ⅱ和Ⅲ之间的连接情况，显然，刚片Ⅱ和Ⅲ之间有链杆 CD 和 EF（相当于一个虚铰）相连。分析结果表明：三个刚片Ⅰ、Ⅱ和Ⅲ用三个不在同一直线上的三个铰（ⅠⅡ)，(ⅠⅢ)，（ⅡⅢ）两两相连，如图 2-12（b）所示，符合组成规则 3，故为几何不变体系，且无多余约束。
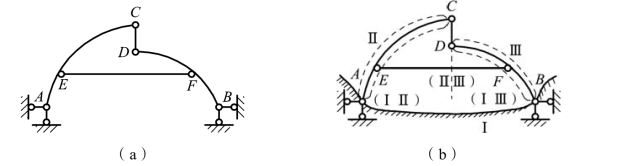
图2-12
由于基础上只有两个连接点A 和B，故亦可不把基础当作刚片，而把它看作连接刚片Ⅱ和Ⅲ的链杆AB，这样，Ⅱ、Ⅲ两个刚片之间，用不交于一点的三根链杆AB，CD 及EF 相连，符合组成规则 2，故为不变体系，且无多余约束。这说明分析的方法尽管可以不同，但正确的结论只有一个。
【例题 2-4】 试分析图 2-13（a）所示体系的几何组成。
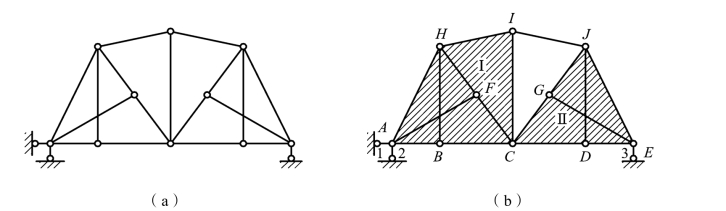
图2-13
解：（1）将铰接三角形 ABH 看作一个刚片，在此刚片上依次增加二元片AFH、BCF、CIH 组成几何不变体系，设为刚片Ⅰ；同理可得到刚片Ⅱ。两刚片由铰 C 和杆 IJ 连接，根据规则 2 可知，体系为几何不变体，且无多余约束，作为一个大刚片。如图 2-13（b）所示。
（2）整个大刚片与基础用不交于一点的三根支杆 1、2、3 相连，组成几何不变且无多余约束的体系。因此，整个体系几何不变且无多余约束。
【例题 2-5】 试对图 2-14（a）所示体系进行几何组成分析。(https://www.chuimin.cn)
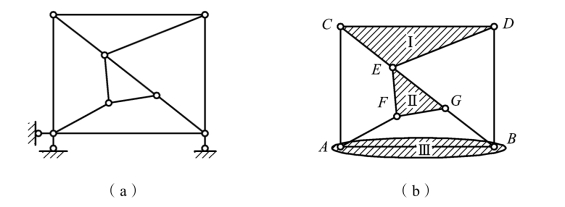
图2-14
解：由于与基础只有三根链杆连接，所以可以直接分析上部体系［见图 2-14（b）］。铰接三角形 CED 为刚片Ⅰ，铰接三角形 EFG 为刚片Ⅱ，杆 AB 为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ用铰 E 相连，刚片Ⅰ与刚片Ⅲ是由杆 AC 和杆 BD 相连，虚铰在无穷远处，而刚片Ⅱ与刚片Ⅲ是由杆 AF 和杆 BG 相连，虚铰在 BG 延长线上，且三铰不共线，故体系为几何不变体，且无多余约束。
【例题 2-6】 试分析图 2-15（a）所示体系的几何组成。
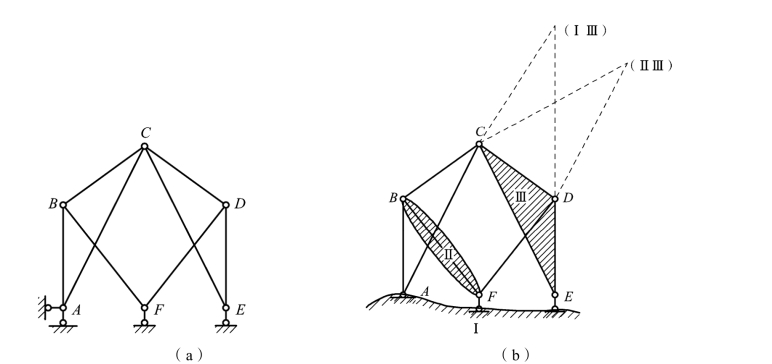
图2-15
解：将固定铰支座换为单铰，如图 2-15（b）所示，由于与基础的约束多于三个，故基础作为刚片Ⅰ。链杆BF 为刚片Ⅱ，铰接三角形CDE 为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由杆AB和支杆F 相连，虚铰在无穷远处，刚片Ⅰ与刚片Ⅲ是由杆AC 和支杆E 相连，虚铰在两杆的延长线的交点处，而刚片Ⅱ与刚片Ⅲ是由杆BC 和杆FD 相连，虚铰在两杆的延长线的交点处。此时，三铰不共线，该体系为几何不变体，且无多余约束。
【例题 2-7】 试对图 2-16（a）所示体系做几何组成分析。
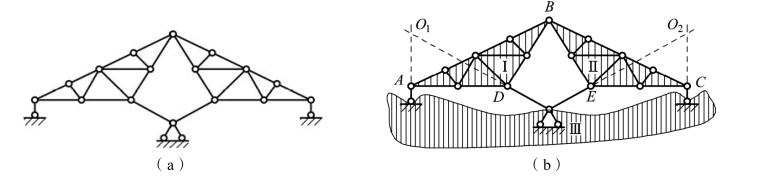
图2-16
解：本题中体系与基础有四根支座链杆，应与基础一起作为一个整体来考虑。
按照例题 2-4 的分析方法，可将ABD 部分作为刚片Ⅰ，BCE 部分作为刚片Ⅱ，取基础作为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ由铰B 相连，刚片Ⅰ与刚片Ⅲ由两根链杆相连，其延长线交于虚铰O1，刚片Ⅱ与刚片Ⅲ由两根链杆相连，其延长线交于虚铰O2。则此三个刚片用铰B 和虚铰O1、O2两两相连，如图2-16（b）所示。如果铰B 和虚铰O1、O2不在同一条直线上，则此体系为无多余约束的几何不变体系；如果此三铰在同一条直线上，则为瞬变体系。
相关文章
- 详细阅读
-
平面几何分析的组成结构详细阅读
对一个平面体系进行几何组成分析时，其可能的最终结果共有四种情况：几何不变体系，且无多余约束；几何不变体系，且有多余约束；常变体系；瞬变体系。在进行平面体系的几何组成分析时，一定要注意每根杆件使用且只能使用一次。由三刚片规则可知，它们所组成的体系是几何不变体系，并且没有多余约束。试对图11-24所示的体系进行几何组成分析。......
2025-09-29
-
平面力系合成的几何法及平衡条件详细阅读
、Fn 组成的平面汇交力系。因此，平面汇交力系平衡的充分与必要的几何条件是：力的多边形自行封闭。图3-8平面汇交力系平衡的几何条件平面汇交力系；平面汇交力系合成；力多边形自行封闭用几何法解题所获得解答的精确程度受作图质量的影响。......
2025-09-29
-
初中数学教学：图形与几何公理化体系与欧氏几何详细阅读
《标准（实验稿）》中“空间与图形”的公理化体系的呈现采用课程形态的公理化体系，这是较为合理的，因为作为“空间与图形”的公理化体系应该是教育形态的公理化体系。另外，《标准（实验稿）》对“空间与图形”的呈现又体现了从点到线到面再到体，即从部分到整体的展开过程。课程标准依然坚持了这种公理化体系，并且在证明方面的要求上有所加强。......
2025-09-29
-
几何不变体系的组成规则详细阅读
图11-15二元体利用二元体规则可以使某些体系的几何组成分析得到简化，也可以直接对某些体系进行几何组成分析。由二元体规则可知，此体系是几何不变体系，并且没有多余约束。然后，将其视为一个更大刚片，它与BC杆再用铰B和不通过该铰的链杆2相连，又组成几何不变体系，且没有多余约束。......
2025-09-29
-
立体图形：两平面相交的几何模型详细阅读
两平面立体相交，其相贯线在一般情况下是封闭的空间折线，但有时也会是平面多边形。从图4-17中可以看出，相贯线（折线）上任一段直线都是甲平面立体的一个棱面与乙立体的一个棱面的交线。因此，求作两平面立体相贯线，实质上仍归结为求直线与平面的交点，以及求平面与平面交线的问题。求直立三棱柱与水平三棱柱的相贯线，如图4-17所示。......
2025-09-29
-
实例分析：包容、检验、合格条件和几何公差详细阅读
3）包容要求的实例分析对图4-33做出解释。④检验与合格条件。图4-34最大实体要求动态公差图；标注标记当基准也适用最大实体要求时，则在几何公差框格内的基准字母后面也加写，如图4-35所示。......
2025-09-29
-
平面与曲面的相交：立体几何优化详细阅读
平面立体与曲面立体的表面交线，一般是由数段平面曲线组合而成的空间曲线，如图4-18所示。因此，求作平面立体与曲面立体的相贯线，可归结为求作平面与曲面立体的截交线和求直线（棱线）与曲面立体表面的交点。其中除左边的棱面AB完全与半球相交外，其他两个棱面只部分与半球相交。因此，本题只需再作出相贯线的正面投影及侧面投影即可。......
2025-09-29
相关推荐