图3.14两直线交叉判断交叉两直线重影点的可见性：如图3.15所示，Ⅰ、Ⅱ两点是H面的重影点，从V面投影可得Ⅰ点在Ⅱ点的上方为可见点，Ⅱ点在Ⅰ点的下方为不可见点，同理，判断Ⅲ、Ⅳ重影点及其可见性。如图3.16所示，已知AB和CD垂直相交，AB是水平线，BC是一般位置线，推导证明ab⊥bc。......
2023-08-30
两曲面体相遇-建筑工程制图与识图
【摘要】：求相贯线实质是求出两曲面立体表面上的一系列共有点，依次连成光滑的曲线，并判别可见性。如图3.43所示，求作两圆柱的相贯线。图3.43两圆柱的相贯线竖直放置的圆柱体在水平投影中具有积聚性，则相贯线在水平投影是已知的。用以上方法再设两个水平辅助面，求出相贯线上一般位置点的三面投影。图3.44圆柱与圆锥的相贯线
曲面体与曲面体相贯，一般是封闭的空间曲线，在特殊情况下可以是平面曲线。求相贯线实质是求出两曲面立体表面上的一系列共有点，依次连成光滑的曲线，并判别可见性。求解方法有表面取点法和辅助平面法。
【例3.14】 如图3.43（a）所示，求作两圆柱的相贯线。
【分析】 两曲面立体相交，如果其中一个立体的某投影有积聚性，则相贯线的该投影是已知的，其他投影可以用曲面立体表面上取点的方法求出。
图3.43 两圆柱的相贯线
【解】
（1）竖直放置的圆柱体在水平投影中具有积聚性，则相贯线在水平投影是已知的。横放的圆柱体在侧面投影中具有积聚性，则相贯线在侧面投影中已知。
（2）求特殊点。在相贯线的水平投影中标出曲线的最高点1、2，最低点3、4，1、2、3、4四个点都在转向轮廓线上，根据线上取点，作出四点的侧面投影，进而求得四点的正面投影。
（3）求一般点。在相贯线的水平投影中标出曲线的一般位置点5、6、7、8四个点，四点尽量对称，方便作图，根据线上取点，作出四点的侧面投影，进而求得四点的正面投影。
（4）整理轮廓线，正面投影中的相贯线是前后对称重叠，详见图3.43（b）。
【例3.15】 如图3.44（a）所示，求圆锥与圆柱的相贯线。
【分析】 本题只给出相贯线的侧面投影，无法用表面取点法求得，可以采用辅助平面法。选择辅助平面的原则：应使辅助平面与两个曲面立体表面交线的投影都为最简单的线条（直线或圆）。
【解】
（1）求特殊点。圆柱的侧面投影有积聚性，相贯线与圆柱的侧面投影重合。相贯线的最高点Ⅰ为圆柱最上面素线与圆锥的交点，最低点Ⅱ为圆柱最下面的素线与圆锥的交点，点Ⅰ、Ⅱ的正面投影和水平投影均直接作出。点Ⅲ为圆柱最前面素线与圆锥的交点，用一水平面过点3″切割圆柱和圆锥，点Ⅲ就是截交线的交点，在侧面投影中量取纬圆半径，于水平面中作一纬圆，此为圆锥被平面切割后产生的截交线，它与圆柱前后两条轮廓线的两个交点即为所求。进而求出正面投影。
（2）求一般点。用以上方法再设两个水平辅助面，求出相贯线上一般位置点的三面投影。
（3）连点并判断可见性。相贯线的水平投影在圆柱上部分可见，下部分不可见为虚线，正面投影前部分可见，后部分不可见，前后重合，补齐剩下的轮廓线。具体作图过程见图3.44（b），作图结果见图3.44（c）所示。
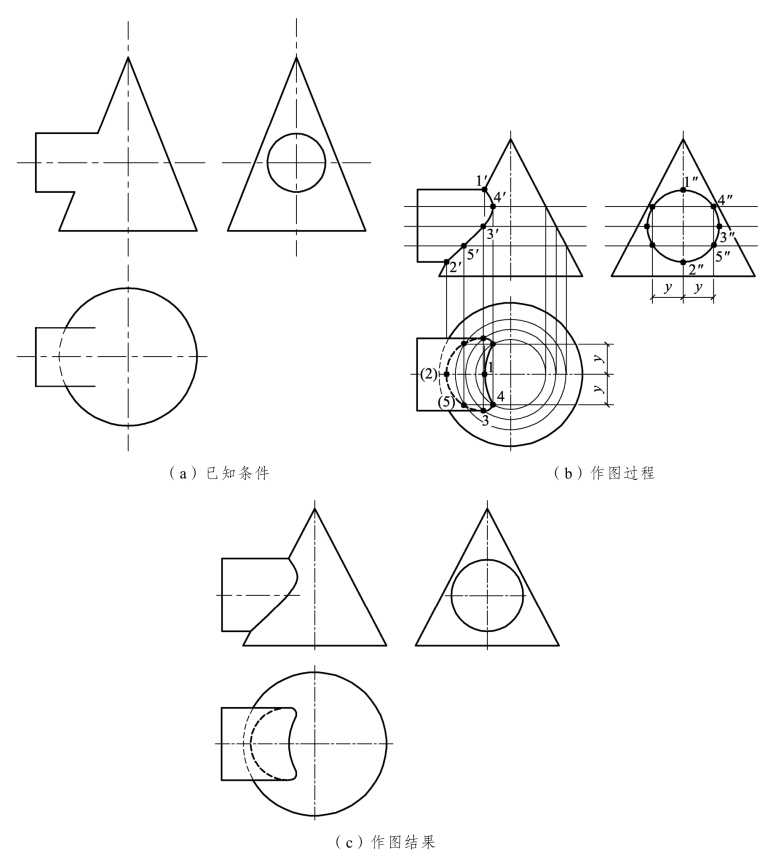
图3.44 圆柱与圆锥的相贯线
有关建筑工程制图与识图：含建筑设备工程识图的文章
- 详细阅读
-
平面体与曲面体在建筑工程制图中的相交详细阅读
平面体与曲面体的相贯线由平面曲线段或平面曲线与直线段的组成。因此，经常把求平面体与曲面体的相贯线问题，转化为求贯穿点问题。求解平面体与曲面体相贯线的方法：求平面与曲面体的截交线；求棱线与曲面立体的贯穿点或曲面立体的轮廓素线与平面立体棱面的贯穿点。如图3.42所示，求三棱柱与圆锥的相贯线。解题前应先分析平面立体有哪些棱面参与了相贯，以避免作图的盲目性。......
2023-08-30
-
建筑工程制图与识图：包含设备工程识图详细阅读
表8.1给水排水施工图的线型2.比例给水排水工程常用比例见表8.2。表8.2给水排水工程常用比例注：① 在管道纵断面图中，竖向与纵向可采用不同的组合比例。图8.1平面图管道标高表示方法轴测图中，管道标高如图8.2所示。当一种系统的立管数量多于一根时，应按阿拉伯数字进行编号，如图8.6图8.6立管表示方法6.常用图例给水排水施工图常用图例如表8.3所示。......
2023-08-30
-
两平面体相交-建筑工程制图与识图：含建筑设备详细阅读
一般情况，平面体的相贯线是封闭的空间折线，特殊情况下可以是不封闭的空间折线或封闭的平面多边形。如图3.41所示，求两个三棱柱的相贯线。图3.41两三棱柱相贯相贯线的水平投影和侧面投影是已知的，竖直的三棱柱的水平投影有积聚性，所以相贯线的水平投影积聚在竖直三棱柱与横放三棱柱相交的部分。分析两立体为互贯，定性判别相贯线的形状为一组空间折线的相贯线。......
2023-08-30
-
房屋组成：建筑工程制图与识图详细阅读
图6.1房屋的组成1.基础基础位于墙或柱的下部，属于承重构件，起承重作用，并将全部荷载传递给地基。两端的横墙通常称为山墙。此外，房屋的正前方一般还设台阶及雨棚；屋面周围有女儿墙。......
2023-08-30
- 详细阅读
-
智能建筑工程：建筑工程制图与识图详细阅读
智能建筑工程施工图的内容与建筑电气工程施工图基本相同，阅读方法也是一样的。熟悉智能建筑工程系统图要比电气照明系统、电气动力系统图更为重要，智能建筑工程各系统图所表示的内容比照明系统图更全面、更具体，基本反映了整个系统的组成及各设备之间的连接关系。见图11.7（见附页）为一层弱电平面图。......
2023-08-30
-
建筑工程制图与识图：基础图示意详细阅读
车间采用排架结构，基础采用钢筋混凝土柱下独立基础，用代号J表示，代号JL和MK分别表示基础梁和车间大门的门框，为了表示清楚各杯型基础、基础梁、门框柱以及它们之间的交接关系，用中实线画出独立基础上的外形轮廓线，粗实线表示预制钢筋混凝土基础梁的平面布置情况。图中涂黑部分表示钢筋混凝土柱的断面。基础的尺寸及受力筋①，根据编号可在表7.4基础表中查出。......
2023-08-30
相关推荐