首页理论教育平面与平面体的相交方法

平面与平面体的相交方法

2023-08-30 理论教育版权反馈

【摘要】：平面与立体表面的交线称为截交线，该平面称为截平面。平面体的截交线为多边形。平面截切平面体时，截交线在一个截平面内，截交线与截平面具有相同的投影特性。当截平面为特殊位置平面，截交线在其相应的投影面上的投影是已知的。图3.36平面立体求截交线如图3.37、所示，已知带切口的三棱锥S-ABC的正面投影，补全水平投影和侧面投影。由的方法求出截平面与棱线交点的投影以及截平面与截平面交点的投影，依次连接可得截交线。

平面与立体表面的交线称为截交线，该平面称为截平面。如图3.34所示，假想用截平面P来截切三棱锥，移去切掉的部分，被截切后的形体称为截断体。

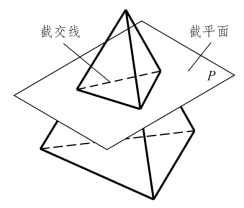
pagenumber_ebook=54,pagenumber_book=46

图3.34　截交线的概念

截交线具有如下性质：

（1）截交线在立体的表面上——表面性。

（2）截交线是截平面和立体表面的共有线——共有性。

（3）截交线是封闭的线条——封闭性。

平面体的截交线为多边形。多边形的边数取决于立体表面的形状及截平面的位置。关键是看立体有几个面参与了相交。

平面截切平面体时，截交线在一个截平面内，截交线与截平面具有相同的投影特性。当截平面为特殊位置平面（截平面至少有一个投影积聚为直线），截交线在其相应的投影面上的投影是已知的。求截交线投影时，可利用已知的积聚性投影。

pagenumber_ebook=55,pagenumber_book=47

图3.35　平面体截交线立体图

【例3.8】　如图3.35所示，已知三棱锥S-ABC被正垂面P截切，求其截交线的投影。

【分析】　如图3.36所示，因截平面是正垂面，所以三棱锥的三条棱线都参与截交，截交点为1、2、3点。1、2、3点属于棱线上的点，可以用线上取点求出其他两面投影。将各投影面上的截交点依次相连并判断截交线的可见性。

【解】　具体作图步骤见图3.36（b）。

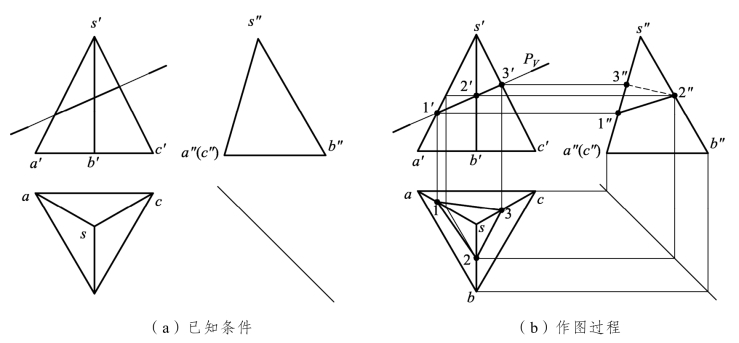
pagenumber_ebook=55,pagenumber_book=47

图3.36　平面立体求截交线

【例3.9】　如图3.37（a）、（b）所示，已知带切口的三棱锥S-ABC的正面投影，补全水平投影和侧面投影。

【分析】　补画三棱锥缺口的投影，实际是画截交线的投影。切口由一个正垂面和一个水平面切割形成。正垂面和水平面在正面的投影积聚为直线，截交线的正面投影是已知的。由【例3.8】的方法求出截平面与棱线交点的投影以及截平面与截平面交点的投影，依次连接可得截交线。

【解】　具体作图步骤见图3.37（c）。

pagenumber_ebook=56,pagenumber_book=48

图3.37　补全带切口的三棱锥

（1）截平面1MN和2MN垂直于正立面，两截平面相交于MN，直线MN垂直于正立面，投影为m′n′。

（2）根据点的从属性，可作出1、2点的水平投影和侧面投影。由1作1 m∥ab、1n∥ac，再分别由m′、n′向下引投影线，作出m、n。由M、N点的两面投影作出第三面投影。

（3）连接m、n，由于mn被三个棱面的水平投影遮挡不可见，所以画虚线，m″n″重合在水平截面的积聚成直线的侧面投影上。

（4）整理轮廓线，加粗实际存在的线，如图3.37（d）。