首页理论教育建筑工程制图与识图：两直线相对位置

建筑工程制图与识图：两直线相对位置

2023-08-30 理论教育版权反馈

【摘要】：图3.14两直线交叉判断交叉两直线重影点的可见性：如图3.15所示，Ⅰ、Ⅱ两点是H面的重影点，从V面投影可得Ⅰ点在Ⅱ点的上方为可见点，Ⅱ点在Ⅰ点的下方为不可见点，同理，判断Ⅲ、Ⅳ重影点及其可见性。如图3.16所示，已知AB和CD垂直相交，AB是水平线，BC是一般位置线，推导证明ab⊥bc。

空间中两直线的相对位置有三种：平行、相交、交叉。其中，平行两直线或相交两直线位于同一个平面上，称为共面直线；交叉两直线不在同一个平面上，称为异面直线。

1.两直线平行

如图3.12所示，空间两直线平行，则他们的同面投影也互相平行。两平行直线投影特性：

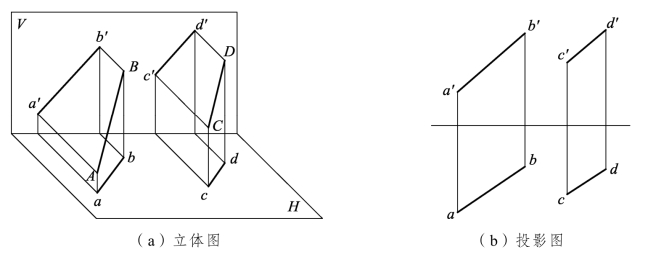
pagenumber_ebook=41,pagenumber_book=33

图3.12　两直线平行

（1）若空间两直线平行，则三对同面投影都平行；

（2）若两直线的同面投影都分别平行，则空间这两条直线必相互平行；

（3）平行两线段的投影长度之比等于其实长之比。

2.两直线相交

如图3.13所示，两直线在空间相交，则各同面投影必相交，且交点符合点的投影规律。

pagenumber_ebook=41,pagenumber_book=33

图3.13　两直线相交

两相交直线投影特性：

（1）若两直线的各同面投影均相交，且交点符合点的投影规律，则他们在空间中相交；

（2）若空间两直线相交，则三对同面投影都相交，且交点连线符合点的投影规律。

3.两直线交叉

如图3.14所示，两直线在空间中既不平行又不相交称为交叉。

两交直线投影特性：

（1）若两直线在空间既不平行也不相交则为交叉；

（2）两交叉直线，它们的同面投影可能相交，但交点不符合点的投影规律。

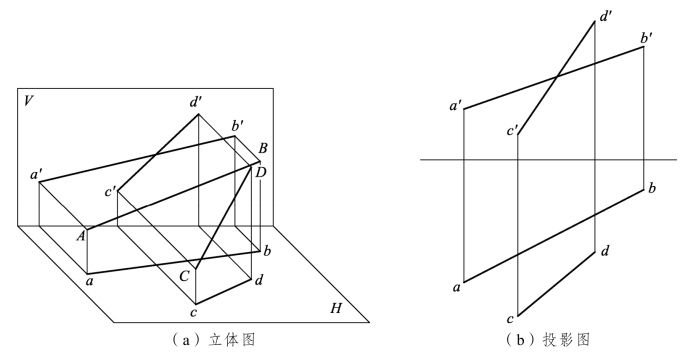
pagenumber_ebook=42,pagenumber_book=34

图3.14　两直线交叉

判断交叉两直线重影点的可见性：

如图3.15所示，Ⅰ、Ⅱ两点是H面的重影点，从V面投影可得Ⅰ点在Ⅱ点的上方为可见点，Ⅱ点在Ⅰ点的下方为不可见点，同理，判断Ⅲ、Ⅳ重影点及其可见性。交叉两直线的同面投影交点是该投影面上重影点的投影，根据投影关系可以判断出重影点的可见性。

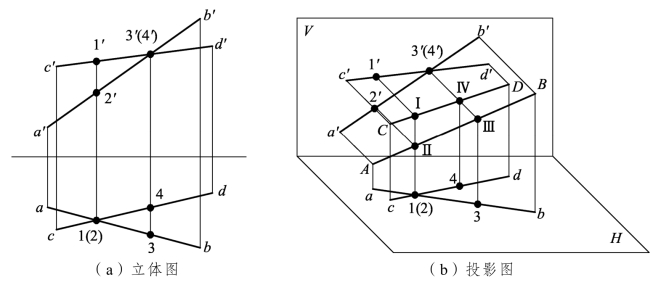
pagenumber_ebook=42,pagenumber_book=34

图3.15　两直线交叉

4.两直线垂直

两直线垂直，其投影适用于直角投影法则：当互相垂直的两直线中至少有一条平行于某个投影面时，则它们在该投影面上的投影也互相垂直。

【例3.2】　如图3.16所示，已知AB和CD垂直相交，AB是水平线，BC是一般位置线，推导证明ab⊥bc。

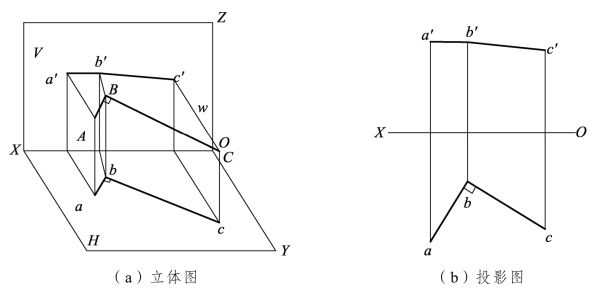
pagenumber_ebook=43,pagenumber_book=35

图3.16　直角投影法则

【解】　因为AB∥H，Bb⊥H，则

AB⊥Bb

又因为AB⊥BC，AB⊥Bb，则

AB⊥BCcb

从ab⊥BC，AB⊥BCcb

可得ab⊥BCcb

故ab⊥bc

直角投影法则，也适用于垂直交叉两直线。当垂直两直线之一为某投影面垂直线时，则另一直线为该投影面的平行线或另两投影面的垂直线。