建筑工程制图：一般位置直线

2025-09-30 理论教育版权反馈

【摘要】：图3.10一般位置直线求实长由此可见：ab＝AB·cosαa′b′＝AB·cosβa″b″＝AB·cosγ从图3.10可归结出直角三角形法求直线的真长和倾角的思路：以直线的某一投影长度为一直角边，以直线两端点到这一投影面的距离差的坐标差为另一直角边，所做出来的直角三角形的斜边就为直线实长，斜边与投影长度的直角边的夹角就是直线与投影面的真实倾角。

对三个投影面H、V、W都倾斜的直线称为一般位置直线。

一般直线的投影特性：

（1）三面投影ab、a′b′、a″b″均倾斜于相应的投影轴。

（2）三面投影不反映直线实长，投影与相应的投影轴之间的夹角不反映直线对投影面倾角的真实大小。

一般位置直线的实长和倾角的求解方法：

如图3.10所示，在投影体系中，空间线段的实际长度称为实长。空间直线相对每个投影面都有倾角。直线与水平面的倾角用α表示，与正立面的倾角用β表示，与侧立面的倾角用γ表示。延长直线AB和投影ab相交于点E，两条线夹角α，在直角三角形BbE平面上，过A作水平线AB0∥ab，则∠AB0B是直角，△AB0B是直角三角形。在直角三角形AB0B中，直角边AB0＝ab；另一条直角边BB0＝bB－aA，就是B点和A点在Z轴上的坐标差ΔZ；斜边是直线AB的真长；斜边与AB0的夹角是倾角α。同理，△AA0B和△AA1B也是直角三角形，AA0＝Δy，AA1＝Δx。(https://www.chuimin.cn)

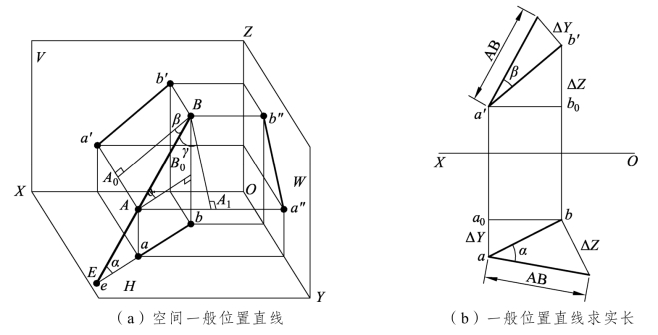
pagenumber_ebook=38,pagenumber_book=30

图3.10　一般位置直线求实长

由此可见：ab＝AB·cosα

a′b′＝AB·cosβ

a″b″＝AB·cosγ

从图3.10可归结出直角三角形法求直线的真长和倾角的思路：以直线的某一投影长度为一直角边，以直线两端点到这一投影面的距离差的坐标差为另一直角边，所做出来的直角三角形的斜边就为直线实长，斜边与投影长度的直角边的夹角就是直线与投影面的真实倾角。

建筑工程制图：一般位置直线

相关推荐