根据投射线形式的不同，将投影法分为中心投影法和平行投影法。
1.中心投影法
投射线从投射影中心发射对物体做投影的方法叫中心投影法，所得的中心投影称作为透视图。中心投影法是投影法的一类，投射线都汇交于一点，如图1.2（a）。
中心投影法特点：
（1）如平行移动物体（几何元素），即改变元素与投射中心或投影面之间的距离、位置，则其投影的大小也随之改变。度量性较差。
（2）在投射中心确定的情况下，空间的一个点在投影面上只存在唯一一个投影。
2.平行投影法
如果把中心投影法的投射中心移至无穷远处，则投射线成为相互平行的直线，如图1.2（b）所示。
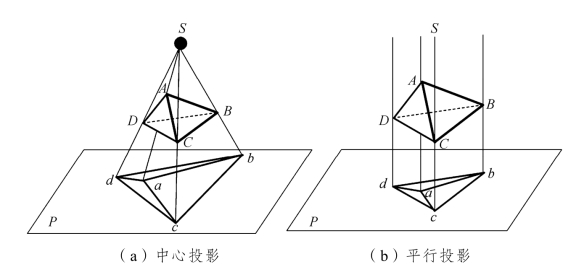
图1.2 投影的分类
根据投射线与投影面的关系，将平行投影法分为斜投影法和正投影法。如图1.3所示，投射线倾斜于投影面，称为斜投影法；投射线与投影面垂直时，称为正投影法。工程图样大多数采用正投影法。正投影法更简单，而且角度唯一。
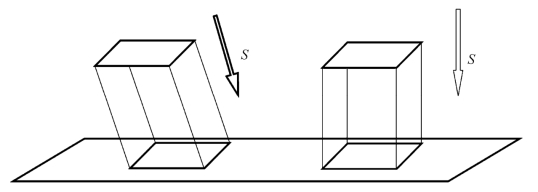
图1.3 平行投影的分类
平行投影法的性质：
（1）类似性（相仿性）：一般情况下，平面形的投影都要发生变形，但投影形状总与原形相仿。所以点的投影仍然是点，直线的投影一般还是直线，平面图形的投影一般是原图形的类似形。
（2）真实性（实形性）：当元素平行于投影面时，其投射反映元素的真实性。当直线平行于投影面时，其投影反映实长；当平面平行于投影面时，其投影反映实形。
（3）积聚性：当直线平行于投射方向时，直线的投影为点；当平面平行于投射方向时，其投影为直线。
（4）定比性：若点在直线上，则点的投影必在直线的同面投影上。若点将直线分为两段，则两段的实长之比等于其投影长度之比。如图1.4中，AC∶CB＝ac∶cb。
（5）平行性：若空间两直线互相平行，则其同面投影也互相平行（投影重合为其特例）。二平行线段的空间实长之比等于其投影长度之比。如图1.5中，AB∶CD＝ab∶cd。
（6）从属性：若点在直线上，则该点的投影一定在该直线的投影上。
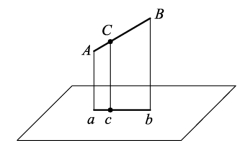
图1.4 定比性
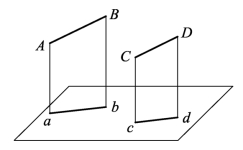
图1.5 平行性
有关建筑工程制图与识图：含建筑设备工程识图的文章
电缆的结构、特点和用途可通过型号表示出来，其型号表示方法如表11.3。例如：WD01 YJV-5SC80-WS3.5，表示电缆参照代号为WD01，电缆型号为YJV，电缆根数为5，电缆导体根数与截面为，敷设方式为穿管直径80 mm的焊接钢管沿墙敷设，线缆敷设距地高度为3.5 m。表11.5线缆敷设方式标注的文字符号表11.6线缆敷设部位标注的文字符号3.照明灯具的标注灯具的标注是在灯具旁按灯具标注规定标注灯具数量、型号、灯具中的光源数量和容量、悬挂高度及安装方式。......
2023-08-30
一般情况，平面体的相贯线是封闭的空间折线，特殊情况下可以是不封闭的空间折线或封闭的平面多边形。如图3.41所示，求两个三棱柱的相贯线。图3.41两三棱柱相贯相贯线的水平投影和侧面投影是已知的，竖直的三棱柱的水平投影有积聚性，所以相贯线的水平投影积聚在竖直三棱柱与横放三棱柱相交的部分。分析两立体为互贯，定性判别相贯线的形状为一组空间折线的相贯线。......
2023-08-30
如表3.6所列，截平面与圆锥体轴线的相对位置不同，截交线有5种情况：截平面与圆锥体轴线垂直，截交线为一个圆；截交线与圆锥体轴线倾斜并与所有素线相交，截交线为一个椭圆；截平面与圆锥体一条素线平行，截交线为一抛物线和直线围成的图形；截平面与圆锥体轴线平行，截交线为一双曲线和直线围成的图形；截平面通过圆锥体的锥顶，截交线为等腰三角形。表3.6圆锥体截交线的5种情况如图3.39所示，求带切口圆锥体的投影。......
2023-08-30
表8.1给水排水施工图的线型2.比例给水排水工程常用比例见表8.2。表8.2给水排水工程常用比例注：① 在管道纵断面图中，竖向与纵向可采用不同的组合比例。图8.1平面图管道标高表示方法轴测图中，管道标高如图8.2所示。当一种系统的立管数量多于一根时，应按阿拉伯数字进行编号，如图8.6图8.6立管表示方法6.常用图例给水排水施工图常用图例如表8.3所示。......
2023-08-30
图6.1房屋的组成1.基础基础位于墙或柱的下部，属于承重构件，起承重作用，并将全部荷载传递给地基。两端的横墙通常称为山墙。此外，房屋的正前方一般还设台阶及雨棚；屋面周围有女儿墙。......
2023-08-30
工程图样是包括建筑工程在内的工程与产品信息的载体，是表达设计思想、进行技术交流的语言，是工程技术部门的一项重要技术文件。到了计算机高度普及的21世纪，人们已经很少使用手工绘制图样，取而代之的是计算机制图，“程序”替代了“手工”，但是基于“画法几何”的基本原理依旧没有改变，在未来社会仍将影响着人们的创作和表达。为协调各个国家制图标准，国际上制订了相关的国际标准，供各个国家制订或修订制图标准时参考。......
2023-08-30
三面投影图的位置为正面投影处于左上方，水平投影在正面投影的正下方，侧面投影在正面投影的正右方。如图1.10所示，空间物体有上下、左右、前后6个方位，但在三面投影图中，每个投影面上的投影反映6个中的4个方位。图1.9三面投影图度量对应关系图1.10三面投影图位置对应关系作图方法。如图1.11所示，根据“长对正、高平齐、宽相等”的“三等”关系和正投影法，画出三面投影图。图1.11三面投影图作图方法......
2023-08-30
相关推荐