系统集成:信息流及信息单元矩阵描述

2023-08-30 理论教育版权反馈

【摘要】：图11-1 系统集成中的信息数据流及传输2.纵向信息数据可以将系统集成中的信息数据及处理方式用n维线性空间的矩阵元表示。系统中不同的监控点所携载的信息可以构成一个信息组，用一个子矩阵块表示。

有些学者对系统集成进行理论描述方面做了很有益的工作，他们这样描述集成系统中的信息流向和数据转换：集成系统信息流分为横向和纵向信息流，纵向信息流是指子系统内部及其与中央集成平台之间的信息流动和融合；横向信息流是指各子系统之间的跨系统联动和融合。信息分为检测和控制信息，监测类信息自底层设备指向中央监控主机方向侧流动；控制类信息自中央监控主机方向指向底层设备方向流动。

1.系统集成中的信息数据流及传输

信息在流经不同网络层级或者完成从一个异构网络流向另外一个异构网络时，常常会伴随着数据组织方式的转变。数据的逻辑表示方法、报文格式或数据类型都可能发生改变。

系统集成中的信息数据流及传输的情况如图11-1所示。

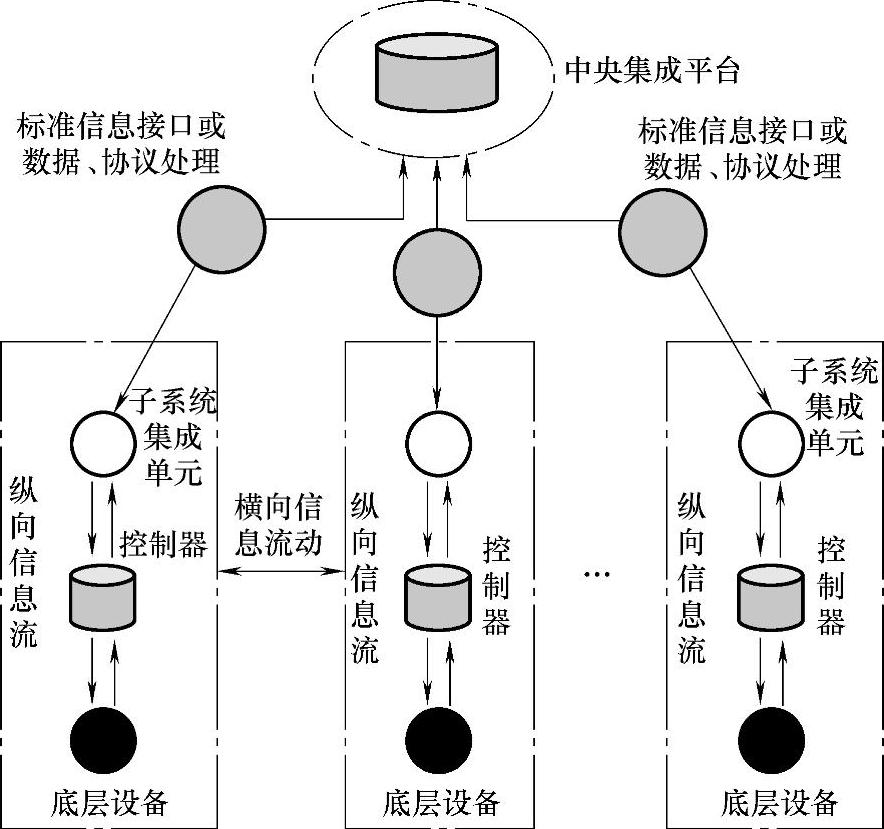
图11-1 系统集成中的信息数据流及传输

2.纵向信息数据

可以将系统集成中的信息数据及处理方式用n维线性空间的矩阵元表示。系统中不同的监控点所携载的信息可以构成一个信息组，用一个子矩阵块表示。

设整个系统有m个子系统，即有一个m维的列向量，系统用Z（m_i）表示：

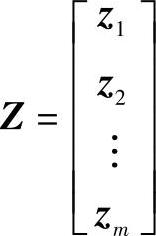
式中 z₁——子系统1；

z₂——子系统2；

…

z_m——子系统m。

也可以表示为

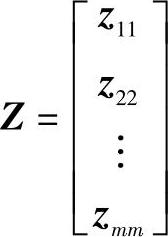
式中 z₁₁——子系统1的监控点信息组，也是一个列向量，具体含有多少个矩阵元由实际系统

决定；

z₂₂——子系统2的监控点信息组；

…

z_mm——子系统m的监控点信息组。

每个子系统可以设置子系统集成单元，接收各个传感器采集的数据信息并进行适当处理，如重复数据较多可以进行数据融合。m个子系统向中央集成平台单向传送待处理的信息数据。每个监测点的数据信息可以用一个属性矩阵来存储。

3.横向信息

m个子系统之间可以进行互通信和互操作的横向信息也可以用一个线性空间中的向量来表示：

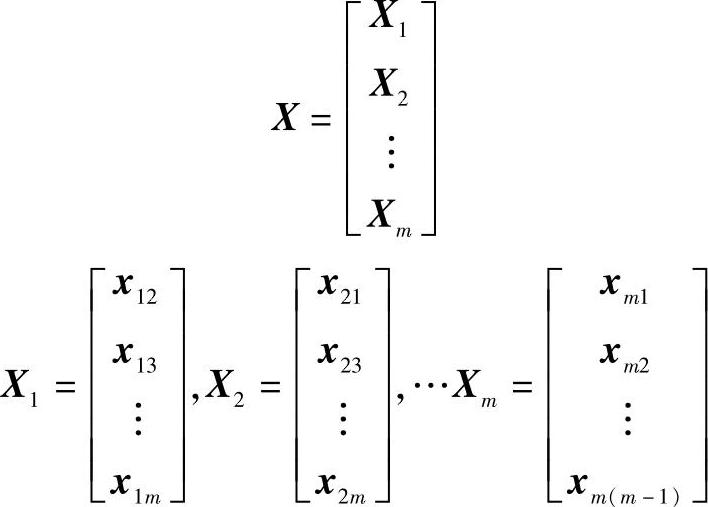
式中 X——m个子系统彼此之间的信息数据横向传递矩阵；

X₁——第1个子系统与其余（m－1）个子系统信息数据交互的矩阵子块；

X₂——第2个子系统与其余（m－1）个子系统信息数据交互的矩阵子块；

x₁₂——第1个子系统与第2个子系统信息数据交互的矩阵子块；

x₁₃——第1个子系统与第3个子系统信息数据交互的矩阵子块。

︙

余类推。

每一个带有控制环节的子系统都有自己的状态空间模型：

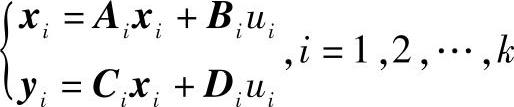
式中 x_i——第i个控制子系统的状态变量；

u_i——第i个控制子系统的外输入；

y_i——第i个控制子系统的输出向量；

A_i、B_i、Ci和D_i——第i个控制子系统的系统矩阵、控制矩阵、输出矩阵和传递矩阵。

各个子系统主要使用常规控制的方式，也可以是智能控制方式。由于空调系统尤其是变风量空调机组及其控制系统是典型的非线性多变量的复杂系统，用常规控制方法实施控制时，当工况发生移动时，一些设定的控制参数就不太适宜新的工况状态了，使用智能控制方法可以很好地应对工况移动造成控制系统控制性能下降的问题，比如PID调节器就是一个典型的例子，PID调节器用于常规控制场所中是很有效的，但对于非线性的多个输入和多个输出的复杂系统，设定好的PID参数随着工况移动而变得不合适了，智能PID调节器的诸参数可以随着工况移动而移动，从而能够有较优良的控制性能。

以上将系统集成的信息数据用数学模型及数据库进行描述及管理的方法有以下优点：

1）有助于系统集成的标准化：没有标准化，不同的系统集成商在集成内容上具有随意性，将会导致系统尽管实现了集成但具有很强大的封闭性，开放性变差。

2）使用数学模型和数据库，将提高系统集成资源的共享，各个不同的BAS有很多的信息数据是完全可以共享的。

3）使用数学模型和数据库有助于降低系统集成设计、施工的难度，因为计算机系统处理数据模型和数据库的效能比人工方式高得多。

系统集成:信息流及信息单元矩阵描述

相关推荐