行车道板计算规范与案例

7.5.1.1 行车道板的力学模型

混凝土梁桥的桥面板是直接承受车辆轮压的混凝土板，它与主梁梁肋和横隔梁联结在一起，既保证了梁的整体作用，又将活载传递于主梁。

对于整体现浇的T形和箱形梁桥，梁肋和横（隔）梁之间的桥面板属于矩形的周边支撑板，如图7.5-1a所示。通常其边长比或长宽比（l_a/l_b）大于或等于2，当有荷载作用于板上时，绝大部分力是由短跨方向（l_b）传递的，因此可近似地按仅由短跨承受荷载的单向板来设计。即仅在短跨方向配置受力主筋，而长跨方向只要配置适当的构造钢筋即可。

同理，对于装配式T形梁桥，其桥面板也存在边长比或长宽比l_a/l_b＞2的关系，如果在两主梁的翼板之间：采用不承担弯矩的铰接缝联结（图7.5-1b）时，则可简化为铰接悬臂板。下面介绍其的计算方法。

《规范》第4.1.1条对板的计算模型的简化有如下规定：四边支撑的板，当长边长度与短边长度之比大于或等于2时，可按短边计算跨径的单向板计算；若该比值小于2时，则应按双向板计算。

7.5.1.2 车轮荷载在板上的分布

作用在桥面上的车轮荷载，通过桥面铺装层扩散分布在钢筋混凝土板面上，车轮与桥面的接触面实际上接近于椭圆，荷载要通过铺装层扩散分布，通常可以偏安全地假定呈45°角扩散分布于混凝土板面上。

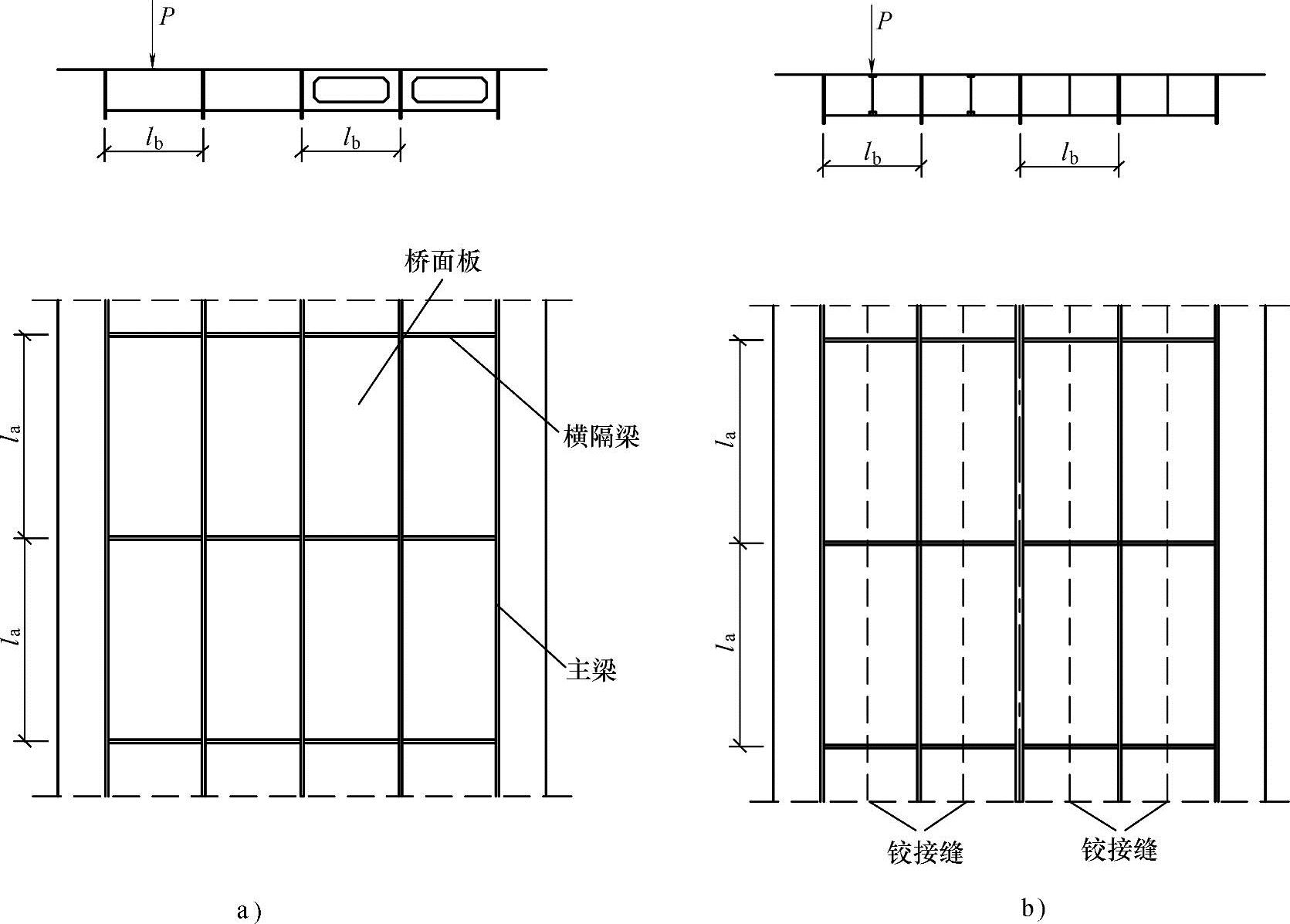
图7.5-1 梁格构造和桥面板的支撑形式

a）整体现浇梁 b）装配式梁桥（翼板间铰接）

假定车轮与桥面的接触面是a₂×b₂的矩形面，此处a₂是车轮（或履带）沿行车方向的着地长度，b₂为车轮（或履带）的宽度，如图7.5-2所示，则最后作用于混凝土桥面板顶面的矩形荷载压力面的边长为

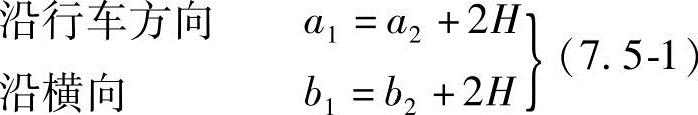
式中 H——铺装层的厚度。

据此，当车辆荷载的后轮作用于桥面板上时，作用于板面上的局部分布荷载为

式中 P——按《公路桥涵设计通用规范》（JTG D60—2004）规定的汽车后轴的轴重。

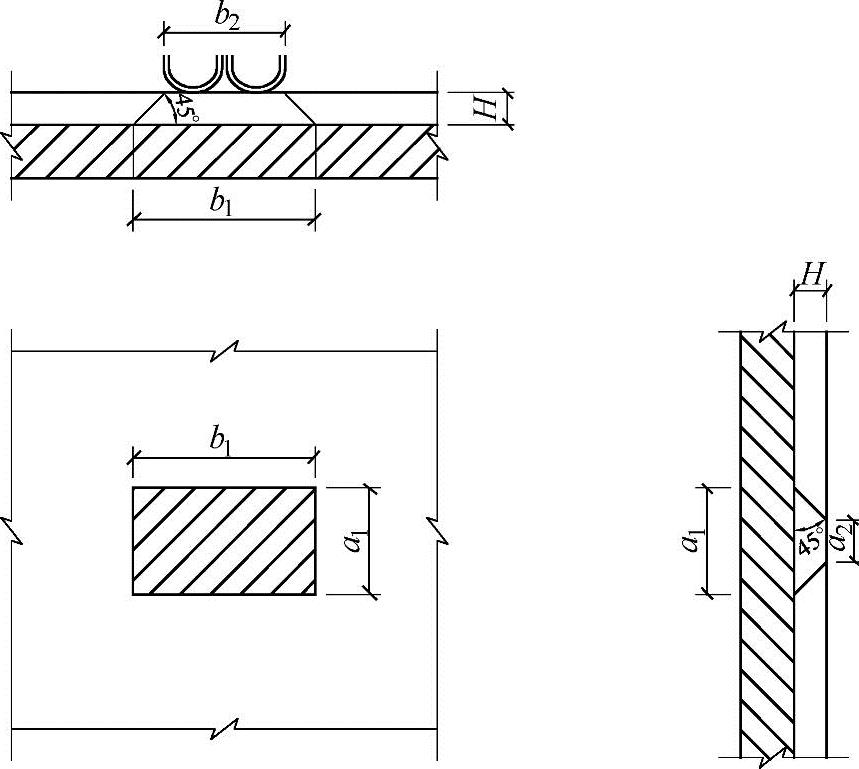
图7.5-2 车辆荷载在板面上的分布

7.5.1.3 板的有效分布宽度

当荷载以a₁×b₁的分布面积作用在板上时，板除了沿计算跨径x方向产生挠曲变形w_x外，沿垂直于计算跨径的y方向也必然发生挠曲变形w_y（图7.5-3a）。这说明荷载作用下不仅使直接承压的宽度为a₁的板条受力，其邻近的板也参与了工作，共同承受车轮荷载所产生的弯矩。

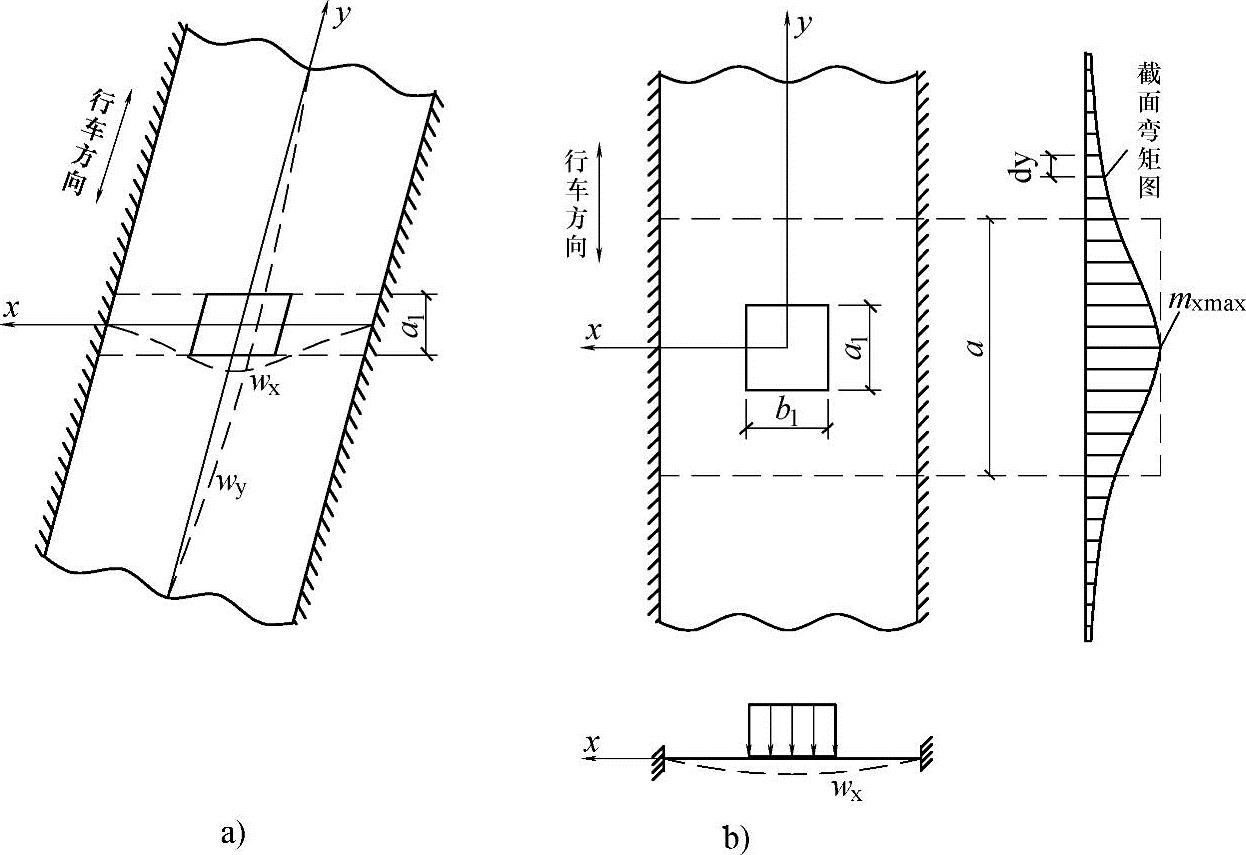
图7.5-3 行车道板的受力状态

为了计算方便，设想以a宽板均匀承受车轮荷载产生的总弯矩（图7.5-3b），即

则得弯矩图形的换算宽度为

式中 M——车轮荷载产生的跨中总弯矩，可直接由结构力学方法计算得到；

m_xmax——荷载中心处的最大单宽弯矩值，精确解需由板的空间计算才能得到。

我们就定义式（7.5-4）的a为板的有效工作宽度或荷载有效分布宽度。用板的有效工作宽度计算板的内力，既满足了弯矩最大值的要求，计算也比较方便。其含义是荷载只在a范围内有效且均匀分布。确定了a就可确定在a×b范围内的荷载集度p。

《规范》第4.1.3条规定，基于大量的理论研究，计算整体单向板时，通过车轮传递到板上的荷载分布宽度应按下列规定计算。

平行于板的跨径方向的荷载分布宽度

b=b₁+2h （7.5-5）

垂直于板的跨径方向的荷载分布宽度：

1）单个车轮在板的跨径中部时

2）多个相同车轮在板的跨径中部时，当各单个车轮按式（7.5-6）计算的荷载分布宽度有重叠时

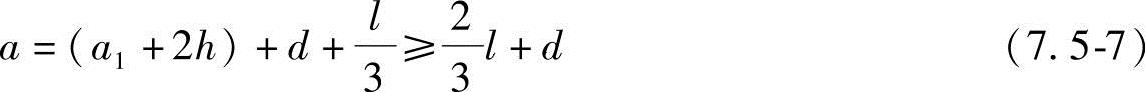
3）车轮在板的支撑处时

a=（a₁+2h）+t （7.5-8）

式中 l——板的计算跨径；

h——铺装层厚度；

t——板的厚度；

d——多个车轮时外轮之间的中距；

a₁、b₁——垂直于板跨和平行于板跨方向的车轮着地尺寸。

4）车轮在板的支撑附近，距支点的距离为x时

a=（a₁+2h）+t+2x （7.5-9）

但不大于车轮在板的跨径中部的分布宽度。

5）按本条算得的所有分布宽度，均不得大于板的全宽度。

6）彼此不相连的预制板，车轮在板内分布宽度不得大于预制板宽度。

7.5.1.4 行车道板的内力计算

1.简支板内力计算

对于实体的矩形行车道板通常由弯矩控制设计。设计时，习惯以每米宽板条来进行计算比较方便，借助板的有效工作宽度，就不难得到作用在每米宽板条上的荷载和其引起的弯矩。

从构造上看，行车道板与主梁梁肋是整体连接在一起的，因此，当板上有荷载作用时，会促使主梁也发生相应的变形，而这种变形又影响到板的内力。如果主梁的抗扭刚度极大，板的工作就接近固端梁（图7.5-4）；反之，如果主梁抗扭刚度极小，板在梁肋支撑处为接近自由转动的铰支座，则板的受力就如多跨连续梁体系。实际上，行车道板和主梁梁肋的支撑条件，既不是固端，也不是铰支，而应该考虑成弹性刚接的受力模式。

图7.5-4 主梁扭转对行车道板受力的影响

鉴于行车道板的受力情况比较复杂，影响的因素比较多，因此，要精确计算板的内力是有一定困难的。通常采用简便的近似方法进行计算。对于弯矩，先算出跨度相同的简支板的跨中弯矩M₀，然后再根据试验及理论分析的数据加以修正。弯矩修正系数可视板厚t和梁肋高度h的比值来选定。

对计算中所用的计算跨径和弯矩修正系数，《规范》第4.1.2条中有明确规定：简支板的计算跨径应为两支撑中心之间的距离。与梁肋整体连接的板，计算弯矩时其计算跨径可取为两肋间的净距加板厚，但不大于两肋中心之间的距离。此时，弯矩可按以下简化方法计算。

（1）支点弯矩

M=-0.7M₀ （7.5-10）

（2）跨中弯矩

1）板厚与梁肋高度比大于或等于1/4时

M=+0.7M₀ （7.5-11）

2）板厚与梁肋高度比小于1/4时

M=+0.5M₀ （7.5-12）

式中 M₀——与计算跨径相同的简支板跨中弯矩。

与梁肋整体连接的板，其计算剪力时的计算跨径可取两肋间净距，剪力按该计算跨径的简支板计算。

简支板的跨中弯矩M₀由两部分组成

M₀=r_GM_0g+r_QM_0p （7.5-13）

式中，r_G为恒载效应分项系数，r_Q为活载效应分项系。

M_0g为每米板宽的跨中恒载弯矩，可由式（7.5-14）计算

此处g为1m宽板条每延米的恒载重量。

M_0p为1m宽简支板条的跨中活载弯矩（图7.5-5），为了找到最大的跨中活载弯矩，首先要确定活载的布置，对汽车荷载受板跨的大小的限制，多数情况下（即l＜1.8m时）只有一个车轮能安排在板跨内，所以该荷载总是被安排在跨中。如果认为轮压为一个集中力，则跨中弯矩为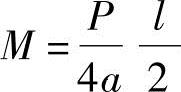；当考虑冲击力的影响后，。由于轮压P/2认为是均匀分布在b的范围，所以计算弯矩时，要考虑这种影响。

式中 P——轴重，对于汽车荷载应取用加重车后轴的轴重计算；

a——板的有效工作宽度；

l——板的计算跨径；

（1+μ）——考虑冲击影响的增大系数，汽车荷载的局部加载及在T形梁、箱形梁悬臂板上的冲击系数采用1.3。

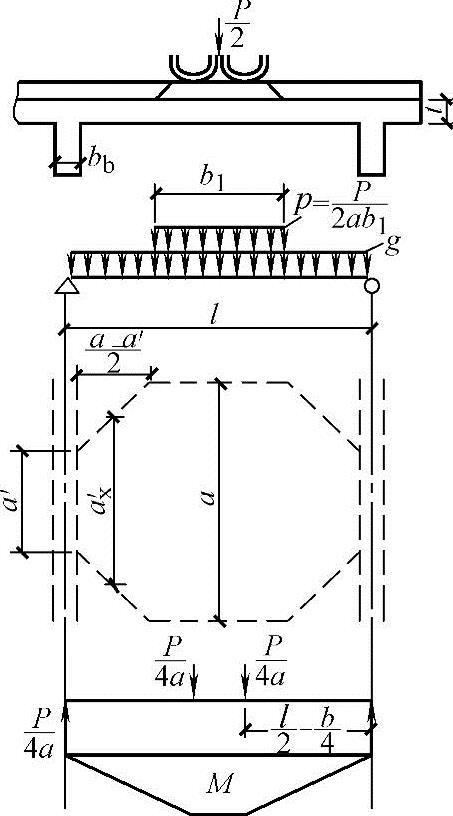
图7.5-5 单向板内力计算图式

如果板的跨径较大，可能还有第二个轮进入跨径内时，可将荷载布置得使跨中弯矩为最大。

【例7.5-1】 一个前轴车轮作用下桥面板的内力计算。主梁跨径为19.5m，桥墩中心距为20m，横隔梁间距4.85m，桥宽为（5×1.6+2×0.75）m=9.5m，主梁为6片。铺装层由沥青面层（3cm）和混凝土垫层（9cm）组成。板厚12cm，主梁肋宽18cm，高130cm，见图7.5-6。桥面荷载为公路—Ⅰ级。试确定板内的弯矩。

图7.5-6 【例7.5-1】图

解答：（1）板类型判别 行车道板平面尺寸：顺桥向L_a=485cm，横桥向L_b=160cm。

所以行车道板为单向板，可取单位宽度来设计。

（2）计算跨度 计算弯矩时，l=L₀+t=（160-18+12）cm=154cm，此处t（t=12cm）为板厚，b_b（b_b=18cm）为梁肋宽，h_b（h_b=130cm）为梁肋高。

剪力计算时

l=L₀=（160-18）cm=142cm

（3）每延米板上恒载g

沥青混凝土面层g₁ 0.03×1.0×23kN/m=0.69kN/m

C25混凝土垫层g₂ 0.09×1.0×24kN/m=2.16kN/m

C25混凝土桥面板g₃ 0.12×1.0×25kN/m=3.0kN/m

合计 g=g₁+g₂+g₃=5.85kN/m

（4）简支条件下每米宽度上恒载产生的板的内力

（5）轮压区域尺寸 汽车前轮的着地长度a₂为20cm，宽度b₂为30cm，如图7.5-6所示，前轴上的压力为30kN，此时桥面板上的轮压区域为

a₁=a₂+2h=（20+2×12）cm=44cm

b₁=b₂+2h=（30+2×12）cm=54cm

此处h为铺装层，由沥青面层和混凝土垫层组成。

h=（3+9）cm=12cm

（6）桥面板荷载有效分布宽度a

1）车轮在板跨中部时，应用式（7.5-6）

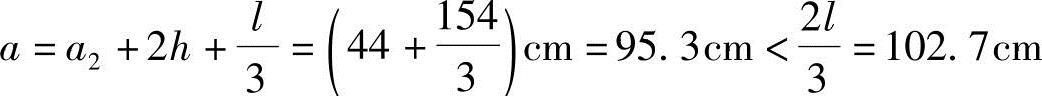，取a=102.7cm。

2）车轮在板跨边端时，应用式（7.5-8）

a=a₂+2h+t=（44+12）cm=56cm

因车辆轮距为1.8m，而桥主梁间距为1.6m，因此，每一跨板内仅只作用有一个车轮，故板内的车轮荷载为P/2。

（7）车辆荷载在桥面板中产生的内力 因为汽车荷载的局部加载的冲击系数采用0.3，所以车轮考虑冲击影响的增大系数1+μ=1.3。

（8）简支梁跨中弯矩M₀ 由式（7.2-9）、式（7.2-10）中的符号说明得永久作用效应的分项系数为1.2，汽车荷载效应的分项系数为1.4。

M₀=（1.2×1.73+1.4×6.03）kN·m=10.52kN·m

（9）最终内力 由于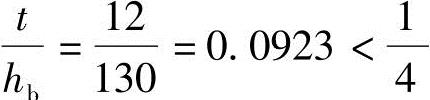，故主梁抗扭能力较大。由式（7.5-10）、式（7.5-12）得：

桥面板跨中弯矩

M_中=0.5M₀=0.5×10.52kN·m=5.26kN·m

桥面板支点弯矩

M_支=-0.7M₀=-0.7×10.52kN·m=-7.36kN·m

2.悬臂板的内力计算

悬臂板在荷载作用下，除了直接承受荷载的板条外，相邻的板条也发生挠曲变形而承受部分荷载。因此，在计算悬臂板内力时，应先计算悬臂板活载的有效分布宽度。垂直于悬臂板跨径方向的车轮荷载分布宽度，当c值（图7.5-7）不大于2.5m时，可按下列公式计算

a=（a₁+2h）+2c （7.5-16）

式中 a——垂直于悬臂板跨径的车轮荷载分布宽度；

a₁——垂直于悬臂板跨径的车轮着地尺寸；

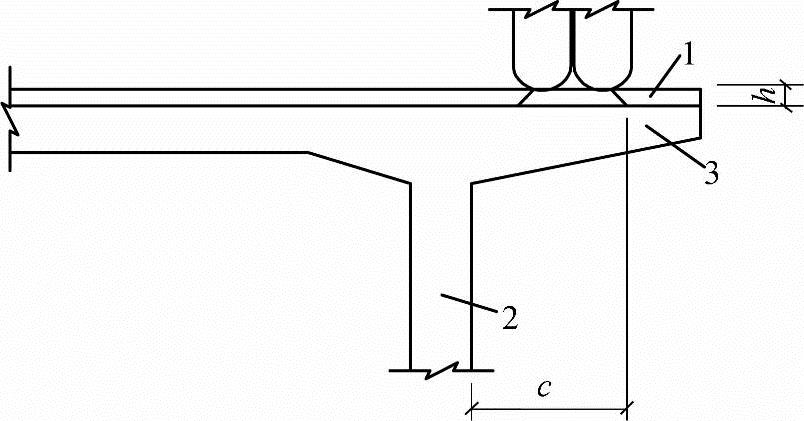
图7.5-7 车轮荷载在悬臂板的分布

1—桥面铺装 2—腹板 3—悬臂板

c——平行于悬臂板跨径的车轮着地尺寸的外缘，通过铺装层45°分布线的外边线至腹板外边缘的距离；

h——铺装层厚度。

计算根部最大弯矩时，应将车轮荷载靠板的边缘布置，此时b=b₁+h，如图7.5-8所示。则恒载和活载弯矩值可由一般公式求得。

悬臂板根部每米宽板条的恒载弯矩（近似值）为

图7.5-8 悬臂板的力学模型

悬臂板根部每米宽板条的活载弯矩为

或

式中 ——汽车荷载作用在每米宽板条上的荷载集度；

l₀——悬臂板的长度。

最后可得1m板条的最大弯矩为

M_A=r_QM_AP+r_GM_Ag

式中 r_G——恒载效应分项系数；

r_Q——活载效应分项系数。

【例7.5-2】 如图7.5-9所示，某公路桥桥面净宽为（8+2×0.50）m，汽车荷载为公路—Ⅱ级。翼缘板带有湿接缝的钢筋混凝土T梁桥，标准跨径为20m，主梁间距2.2m，边板外翼缘1.2m。梁高1.5m，横隔梁间距4.85m，铺装层平均厚度为8cm，铺装层重度γ_铺=24kN/m³，桥面板重度γ_板=25kN/m³，防撞护栏每侧重5kN/m。试计算边板悬臂板的弯矩、剪力。

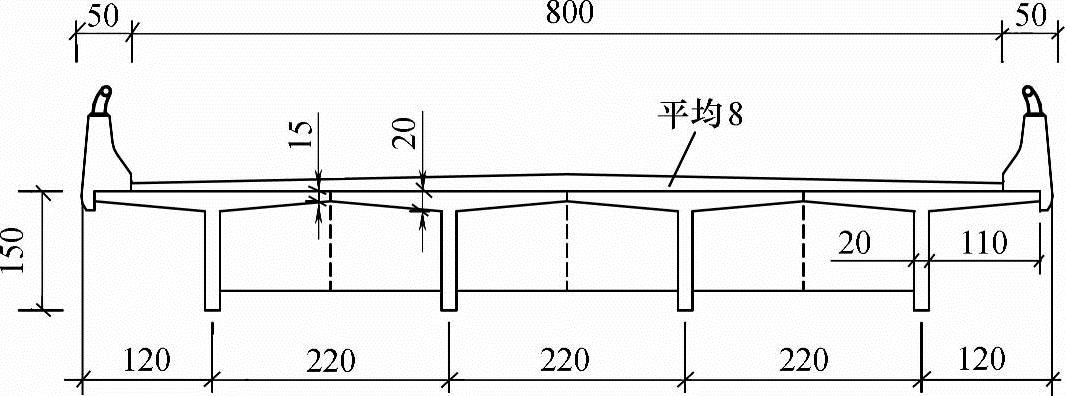
图7.5-9 【例7.5-2】图（尺寸单位：cm）

解答：边主梁外翼缘为嵌固在主梁梁肋上的悬臂板。

（1）板的计算跨径l=1.1m。

（2）恒载集度g。

铺装层g₁ 0.08×1.0×24kN/m=1.92kN/m

混凝土桥面板g₂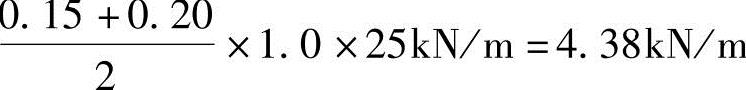

合计 g=g₁+g₂=6.30kN/m

防撞护栏自重：P_护=5×1kN=5kN；

作用点l_护：取外翼缘端部以内0.2m处，即l_护=0.9m。

（3）恒载弯矩、剪力

（4）汽车荷载选用如图7.5-10所示车辆荷载进行计算。

图7.5-10 车辆荷载

1）选取荷载：根据轴距及轴重，采用2×P=2×140kN或2×P=2×120kN或前轴P=30kN计算，应以重轴为主。

2）轮载分布：重轴车轮着地尺寸a₂×b₂=0.2m×0.6m。

经铺装层按45°角扩散后在板顶的分布尺寸

a₁=a₂+2h=（0.2+2×0.08）m=0.36m

b₁=b₂+2h=（0.6+2×0.08）m=0.76m

3）板的有效工作宽度。车轮尽量靠近悬臂端部，如图7.5-11所示。

c=0.48m＜2.5m

a=（a₁+2h）+2c=（0.36+2×0.48）m=1.32m

小于最小轴距1.4m，取后轴，且有效工作宽度无重叠，取用单个车轮的有效工作宽度即可。

4）车轮荷载集度。车轮位于悬臂根部，分布范围a=1.32m，b=0.76m。

车轮荷载集度

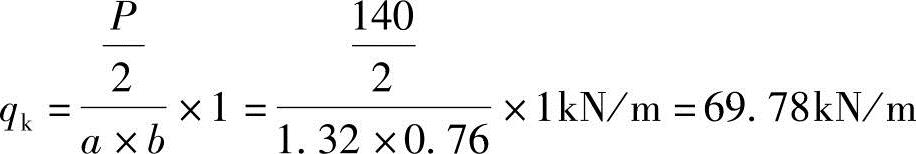
（5）汽车及冲击力弯矩、剪力（取冲击系数μ=0.3）

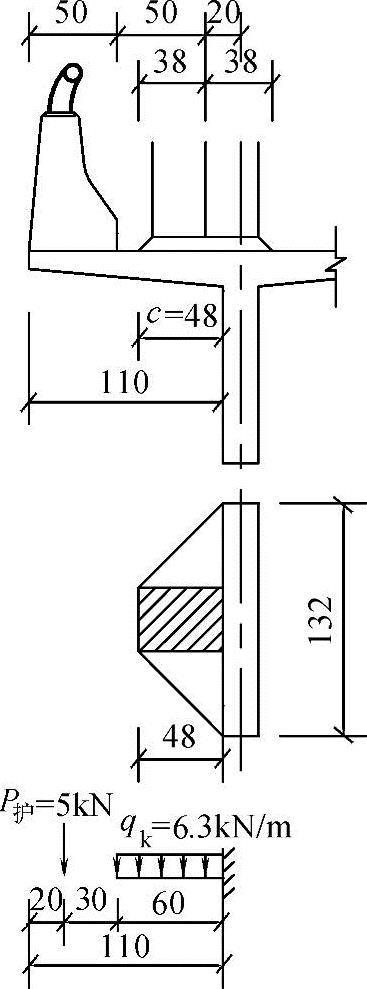
图7.5-11 板的有效工作宽度（尺寸单位：cm）

（6）弯矩组合

M_悬=γ₀（γ_GlM_Gl+γ_QlM_Ql）=1.0×（1.2×5.63+1.4×10.45）kN·m=23.39kN·m

V_悬=γ₀（γ_GlV_Gl+γ_QlV_Ql）=1.0×（1.2×8.78+1.4×43.54）kN=71.49kN

3.铰接悬臂板的内力计算

T形梁翼缘作为行车道板往往用铰接的方式连接，最大弯矩在悬臂根部。

根据计算分析可知，计算活载弯矩M_Ap时，最不利的荷载位置是把车轮荷载对中布置在铰接处，这时铰内的剪力为0，可按悬臂板计算，两相邻悬臂板各承受半个车轮荷载，即P/4，如图7.5-12所示。悬臂板根部每米宽的活载弯矩为

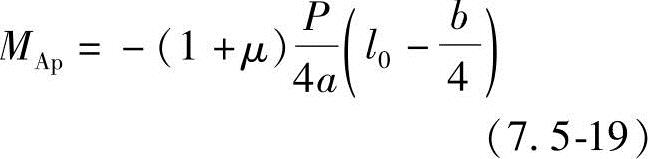
式中 1+μ=1.3。

悬臂板根部每米宽的恒载弯矩为

式中 l₀——铰接悬臂板的净跨径。

图7.5-12 铰接悬臂板的受力图式

悬臂板根部每米宽的最大弯矩为

M=r_QM_Ap+r_GM_Ag （7.5-21）

式中 r_G——恒载效应分项系数；

r_Q——活载效应分项系数。

【例7.5-3】 图7.5-13所示T形梁翼板所构成的铰接悬臂板。设计荷载为公路—Ⅱ级，γ₀=1.0，冲击系数μ=0.3。桥面铺装为5cm沥青混凝土面层（重度为21kN/m³）和15cm防水混凝土垫层（重度为25kN/m³）。计算铰接悬臂板的设计内力。

解答：（1）恒载内力（以顺桥向1m宽的板进行计算）

1）每延米板上的恒载集度。

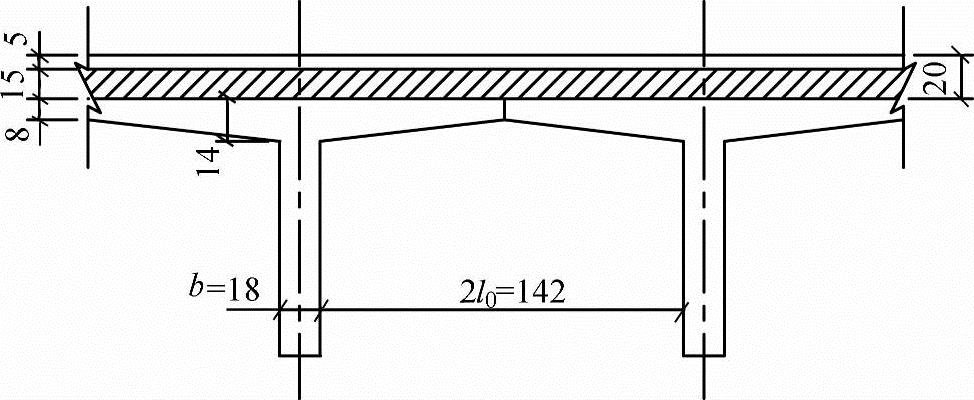
图7.5-13 铰接悬臂行车道板（尺寸单位：cm）

沥青混凝土面层： g₁=0.05×1.0×21kN/m=1.05kN/m

防水混凝土垫层： g₂=0.15×1.0×25kN/m=3.75kN/m

T形梁翼板自重：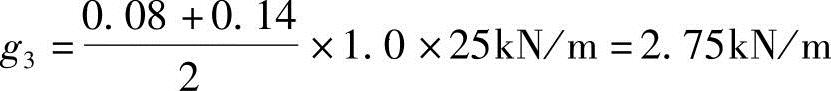

合计 g=∑g_i=7.55kN/m

2）每米宽板条的恒载内力。

弯矩

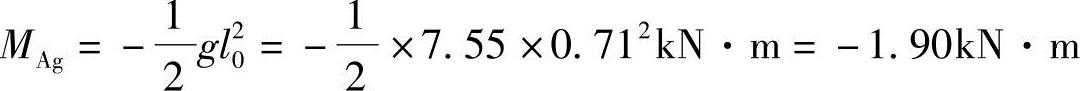
剪力

V_Ag=gl₀=7.55×0.71kN=5.36kN

（2）公路—Ⅱ级车辆荷载产生的内力 将公路—Ⅱ级车辆荷载的两个140kN轴重的后轮（轴间距1.4m）沿桥梁的纵向作用于铰缝轴线上，为最不利荷载。由表7.2-4查得重车后轮的着地长度a₂=0.2m，着地宽度b₂=0.6m，车轮在板上的布置及其压力分布图形如图7.5-14所示，铺装层总厚H=（0.05+0.15）m=0.20m，则板上荷载压力面的边长为

a₁=a₂+2H=（0.2+2×0.20）m=0.6m

b₁=b₂+2H=（0.6+2×0.20）m=1.0m

则铰缝处纵向两个车轮对于悬臂根部的有效分布宽度为

a=a₁+d+2l₀=（0.6+1.4+2×0.71）m=3.42m

作用于每米宽板条上的弯矩为

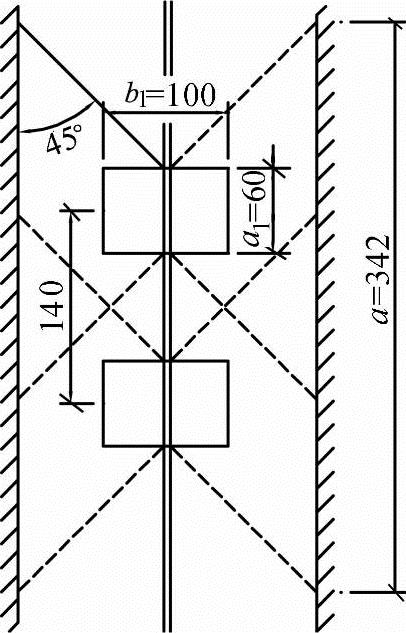
图7.5-14 两个后轴轮载作用于铰缝轴线上（尺寸单位：cm）

P为在有效分布宽度内作用于铰缝的轴重之和，P=140×2kN=280kN。

相应于每米宽板条活载最大弯矩时的每米宽板条上的剪力

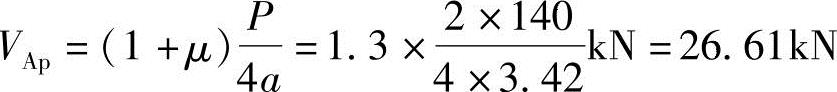
（3）悬臂板根部每米宽的最大弯矩

M=γ₀（γ_AgM_Ag+γ_ApM_Ap）=1.0×（-1.2×1.90-1.4×12.24）kN·m=-19.42kN·m

V=γ₀（γ_AgV_Ag+γ_ApV_Ap）=1.0×（1.2×5.36+1.4×26.61）kN·m=43.69kN·m

7.5.1.5 斜板桥的受力特点

国外学者通过对简支斜板桥进行模型试验，认为可以把斜板的受力性能简单地用一个三跨连续梁相比拟，如图7.5-15所示。具体归纳为如下几点：

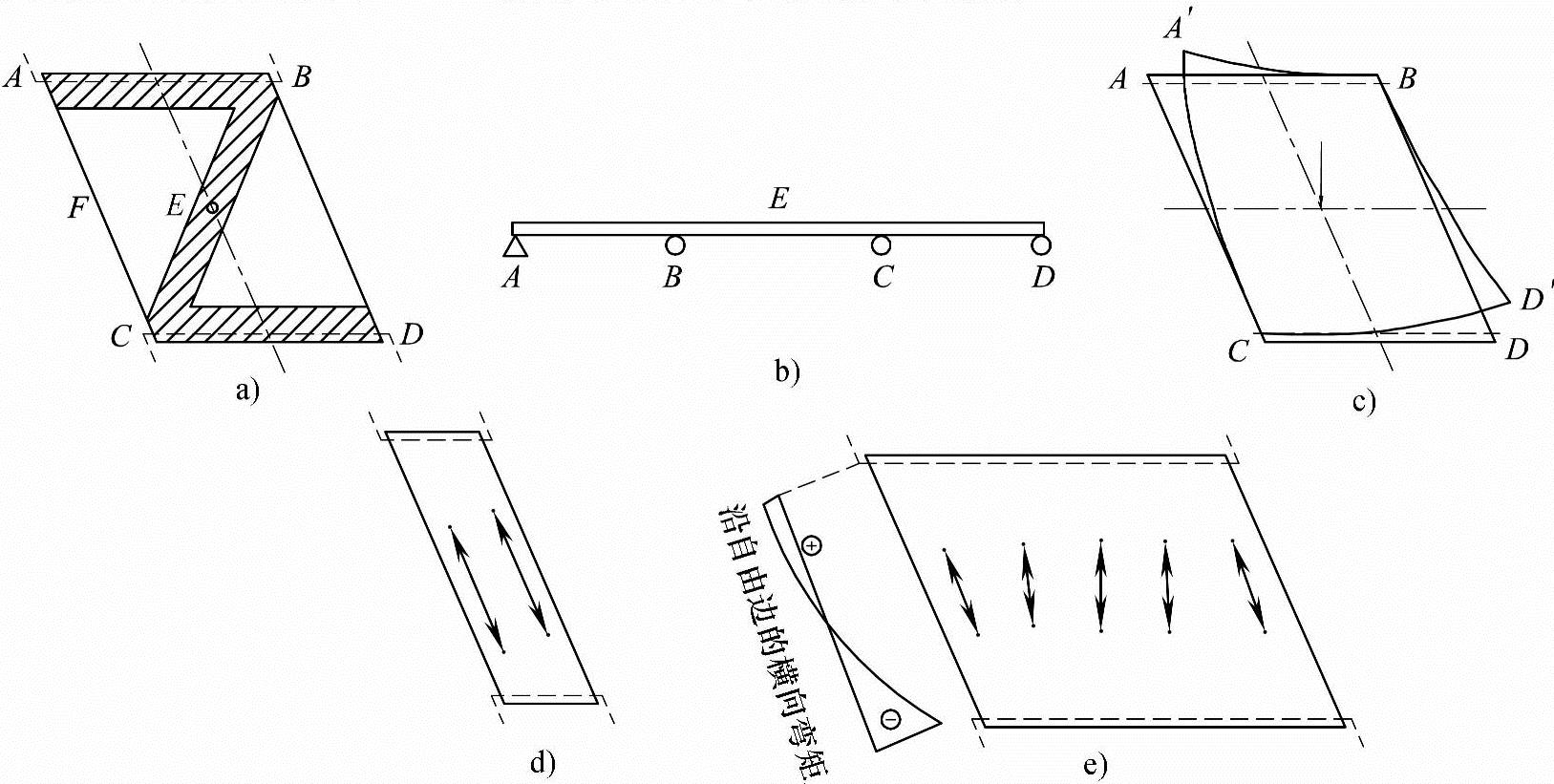
图7.5-15 斜板桥的受力状态

（1）支撑边反力 支撑边的反力是呈不均匀分布的，以钝角B、C处的反力最大，以锐角A、D处的反力最小，甚至可能出现负反力，使锐角向上翘，如图7.5-15c所示。

（2）跨中主弯矩 对于宽跨比较大的斜板，其中心处的主弯矩方向接近与支撑边正交。但在斜板的两侧，则无论斜板宽跨比的大小，其主弯矩方向接近平行自由边，如图7.5-15d、e所示。并且，弯矩值沿板宽分布也是不均匀的，对于均布荷载，中部弯矩值大于两侧；对于集中荷载，则以布载点处为最大。

（3）钝角负弯矩 如同连续梁的中支点截面一样，在钝角B、C处产生负主弯矩，有时它的绝对值比跨中主弯矩还要大，其负主弯矩的方向接近与钝角的二等分线相正交。

（4）横向弯矩 斜板的最大纵向弯矩，虽比同等跨径的直桥要小，但横向弯矩却比同等跨径的直桥要大得多，并且沿自由边的横向弯矩还出现反号，靠近锐角处为正，靠近钝角处为负（图7.5-15e）。

（5）扭矩 图7.5-15c所示的A、D点，有起翘的趋势，如果固定A、D两点，那么将使斜板在两个方向产生扭矩，这也是斜板的一个重要特点，但它的分布十分复杂。

影响斜板桥受力的因素包括以下内容。

（1）斜交角α 斜交角是指桥梁轴线与支撑边垂线的夹角，斜交角大小直接关系到斜桥的受力特性，斜交角越大，斜桥的特点越明显。《规范》规定：当斜交角小于15°时，可以忽略斜交的影响，按正交板桥计算。

（2）宽跨比b/l 设b为垂直于桥轴线方向的桥宽，l为垂直于支撑线的宽跨，宽跨比较大，斜桥相对宽度越大，斜桥的特点越明显；宽跨比较小的斜桥，其跨中受力特点比较靠近正桥，只是在支撑线附近的断面才显示出斜桥的特点。

（3）支撑形式 支座个数的多少、支撑形式的变化，包括横桥向是否可以转动或移动、是否采用弹性支撑，对斜板的内力分布均有明显的影响。

掌握了上述斜板的受力性能后，就可以应用近似方法计算其内力，合理地配置斜板的钢筋。当整体式斜板桥的斜交角（板的支撑轴线的垂直线与桥纵轴线的夹角）不大于15°时，可按正交板计算，计算跨径为：当l/b≤1.3时，按两支撑轴线间垂直距离的正跨径计算；当l/b＞1.3时，按顺桥向纵轴线的斜跨径计算；以上l为斜跨径，b为垂直于桥纵轴线的板宽。装配式铰接斜板桥的预制板块，可按宽为两板边垂直距离、计算跨径为斜跨径的正交板计算。