梁的强度计算包括抗弯强度、抗剪强度、局部承压和折算应力。......
2023-08-28
我国《钢木规范》第1.2.3条~1.2.14条规定:结构构件的内力按弹性受力阶段确定。变形按构件的毛截面计算,不考虑钉(栓)孔削弱的影响。为简化计算,可将桥跨结构划分为若干个平面系统分别计算,但应考虑各个平面系统的共同作用和相互影响。
(1)轴心受拉杆 轴心受拉杆件中,由于钢材的塑性,孔洞边的应力集中现象会趋于均匀,凡带孔受拉杆的强度计算中只核算扣孔净截面上的计算平均应力,限值为材料的基本容许应力[σ]。但其疲劳容许应力,则要考虑应力集中的不利而采用B类(高强螺栓连接)或C类(铆钉连接)的限值规定,详见《钢木规范》表1.2.17。
在承受动荷载的轴心受拉杆件中,疲劳计算肯定是起控制作用的。
(2)轴心受压杆 《钢木规范》中所计算的钢压杆的最大承载力,乃取有初偏心、初弯矩、焊接残余应力和其他初始缺陷的钢压杆的压溃荷载,故又称稳定的极限承载力计算。该荷载是第Ⅱ类稳定问题的临界值。为计算方便,《钢木规范》仍沿袭φ1系数法,纵向弯曲系数φ1根据杆件的长细比λ=l0/r从表7.3-3中查用。使用时应区分构件形式、验算平面和材料的不同。
表7.3-3 轴心受压构件的纵向弯曲系数
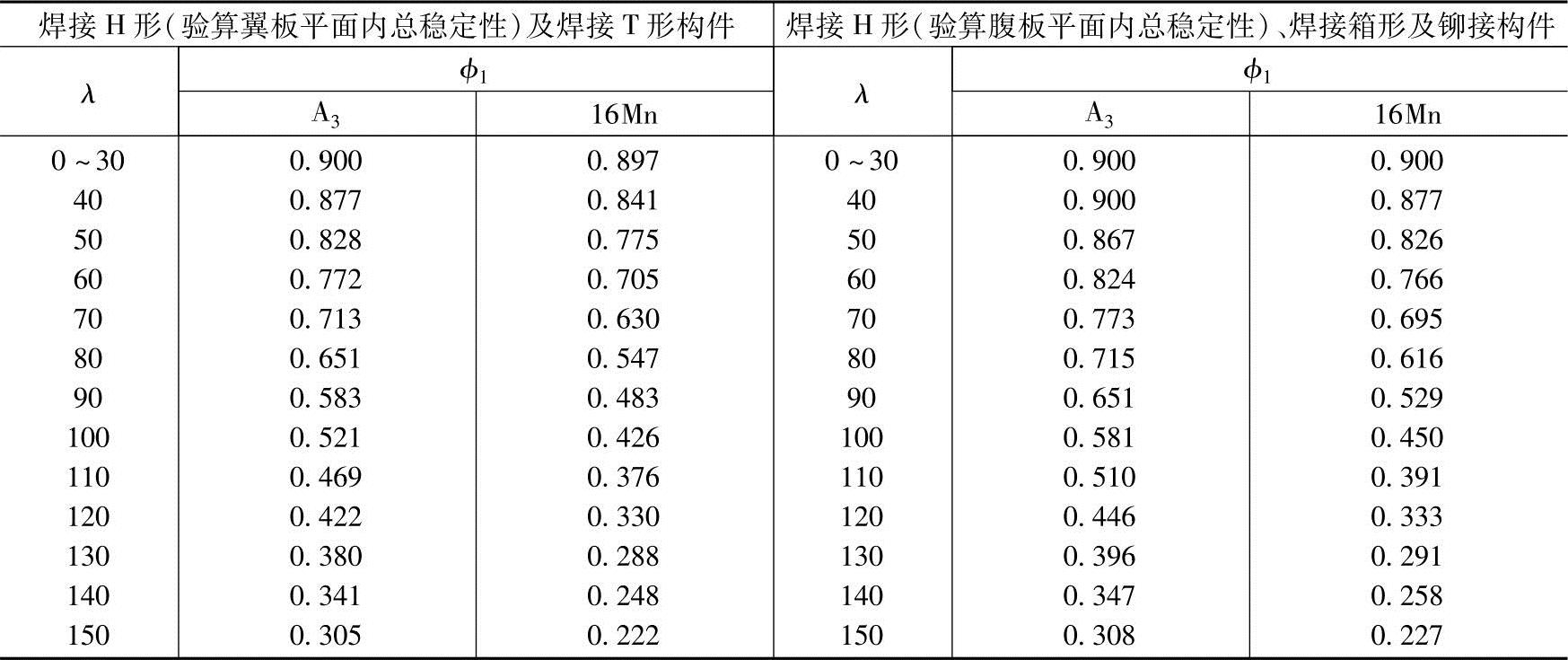
此外,压杆尚应满足板件的宽厚比要求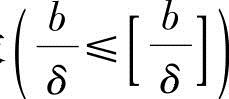 ,以保证它的局部稳定性和整体刚度(λ≤[λ])的要求。
,以保证它的局部稳定性和整体刚度(λ≤[λ])的要求。
(3)受弯构件 钢桥中的受弯构件,主要是受弯实腹钢梁(单向受弯)用于梁式桥或行车道梁。《钢木规范》中仅针对组合式板梁,由于是弹性阶段,故计算并无特色,只是有关的构造,诸如板梁翼缘、腹板、加劲肋、支座等需要加以注意。
至于单梁的整体稳定,由于桥梁结构中以单梁出现承载的情况并不存在,仅在个别架设状态下尚有可能。因此,复习时应当理解梁的丧失整体稳定实际上是由纯弯曲受力突变为侧向弯曲和扭转的耦合受力,这种平衡的失稳仍属第一类稳定,它的临界弯矩Mcr也可用弹性理论求得。现行《钢木规范》是以纯弯梁出现弯曲和扭转屈曲时的弯矩为临界弯矩Mcr,并以相应的跨中截面受压翼缘的最大压应力为临界压应力σcr,而且认定各种钢梁只要受压翼缘的正应力σ≤σcr,梁就不会整体失稳。显然这里并没有考虑梁的诸多缺陷,所以是一种近似算法。为了和压杆的计算取得统一,计算时又引入了梁的纵向弯曲系数φ2,又一次进行了近似处理。φ2为构件只在一个主平面受弯时的纵向弯曲系数(若是压弯杆,可按N=0的情况来确定),再进一步分析时可按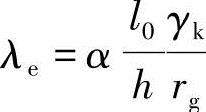 计算长细比λe,并按λe由表7.3-3查得相应的φ1以替代φ2。
计算长细比λe,并按λe由表7.3-3查得相应的φ1以替代φ2。
(4)偏心受压杆 偏心受压杆计算时应满足强度、弯矩平面内的稳定、垂直于弯矩平面的稳定、局部稳定性及刚度的要求。偏心受压杆的强度验算,此处不再赘述。
偏心受压杆的稳定验算,考虑到轴力N和弯矩M的交互作用,《钢木规范》中采用了交叉影响公式

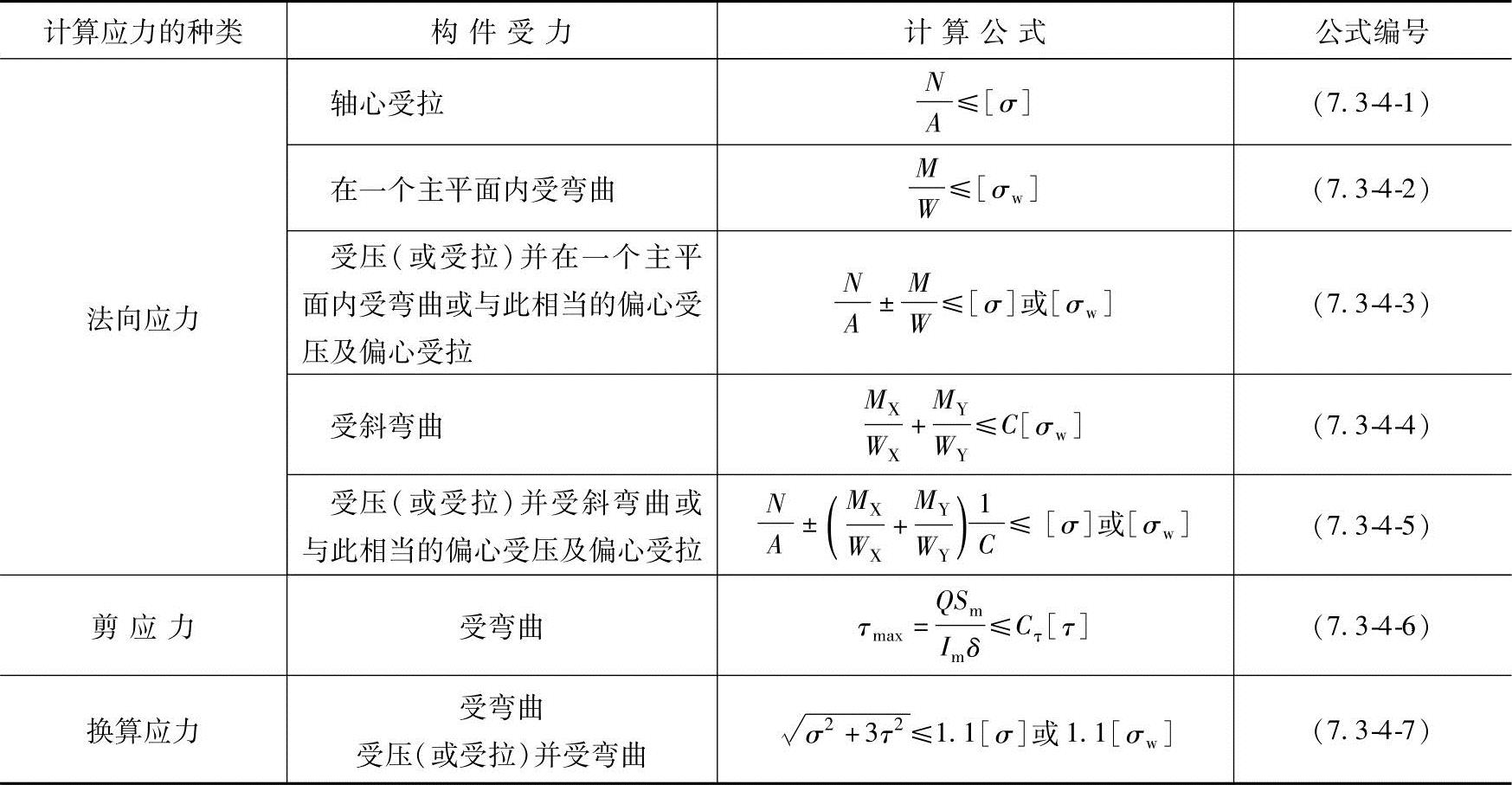
此外,我国《钢木规范》第1.2.15条规定结构构件的强度应按表7.3-4的公式计算。
表7.3-4 强度计算公式
结构构件的总稳定性按表7.3-5的公式计算。
表7.3-5 总稳定性计算公式

有关全国一、二级注册结构工程师专业考试教程的文章

表4.9-5 不同设计使用年限时木材强度设计值和弹性模量的调整系数2.轴心受拉构件的承载力,应按下式验算式中 ft——木材顺纹抗拉强度设计值;N——轴心受拉构件拉力设计值;An——受拉构件的净截面面积,计算An时应扣除分布在150mm长度上的缺孔投影面积。验算挠度和稳定时,可取构件的中央截面,验算抗弯强度时,可取最大弯矩处的截面。表4.9-7 受弯构件挠度限值注:l为受弯构件的计算跨度。......
2023-08-28

一般常用检验电荷来探测、研究电场的性质。、nq,在A点所受到的电场力分别为F、2F、3F、…显然,F/q反映了电场中不同位置电场力的特性。检验电荷在电场中某一点所受电场力F与检验电荷量q的比值,称为该点的电场强度,简称场强,用公式表示为该计算值与假设值相近,说明假设的H3是正确的,表明1kg高压驱动蒸汽可以引射0.75kg的低压蒸汽;换言之,每引射1kg低压水蒸气需用1.33kg的驱动蒸汽。......
2023-06-20

分析:根据式(4-7)知,材料的许用应力为由强度条件式,得由于直杆横截面为圆形,所以得所以圆截面杆的直径至少为18 mm。图4-30简易悬臂吊车分析:求两杆的轴力。根据轴向拉(压)杆的强度条件,AB、BC 杆的最大应力为可见BC 杆的最大工作应力超过了材料的许用应力,所以此结构不安全。根据钢杆AB 的强度要求,有根据木杆BC 的强度要求,有可见,吊车的最大起吊量即许用载荷为FG,其值为40.4 kN。......
2023-06-19

金属基础常专用于直线塔,如图351所示。主柱强度为:图351金属基础式中A2——主柱角钢断面积;N——作用于立柱上的轴向力;Mx、My——作用于主柱上正面和侧面的弯矩;Wx、Wy——主柱角钢平行轴断面系数;[σ]——钢材允许应力。1)a—a构件式中P0——作用于构件内的轴向力,;θ1——斜撑与水平材的夹角;Ma——作用于构件上的弯矩,。......
2023-06-29

表4.8-5 砖砌体强度的正应力影响系数注:σ0为对应于重力荷载代表值的砌体截面平均压应力。表4.8-7 砖砌体房屋构造柱设置要求注:1.较大洞口,内墙指不小于2.1m的洞口;外墙在内外墙交接处已设置构造柱时允许适当放宽,但洞侧墙体应加强。房屋高度和层数接近表4.8-1的限值时,横墙内的构造柱间距不宜大于层高的2倍,下部1/3楼层的构造柱间距适当减小;当外纵墙开间大于3.9m时,应另设加强措施,内纵墙的构造柱间距不宜大于4.2m。......
2023-08-28

受弯构件的抗剪计算 受弯构件的剪力V假定由腹板承受,剪切强度应符合下式要求:V≤hwtwfv 式中 hw、tw——腹板高度和厚度;fv——钢材抗剪强度设计值。压弯构件的压力N不应大于0.6Anf,其剪切强度应符合式的要求。φx、N′Ex和βmx计算参照第3.3.8节相关内容。采用塑性设计法对柱AB进行验算。......
2023-08-28
相关推荐