5.9.5桩基承台设计与计算方法

2023-08-28 理论教育版权反馈

【摘要】：桩承台应采用钢筋混凝土材料，采用现场浇筑施工。柱下桩基承台的弯矩按以下简化计算方法确定。此时承台板的抗冲切强度按《规范》规定计算。图5.9-9 承台斜截面受剪计算示意图《规范》规定：柱下桩基础独立承台应分别对柱边和桩边、变阶处和桩边连线形成的斜截面进行受剪计算。

1.桩基础承台的作用

桩基础承台的作用是将多根桩连接成整体，共同承受上部荷载；将上部结构荷载通过桩承台传递到各桩的顶部；桩基承台相当于一个浅基础，因此桩基承台本身具有类似于浅基础的承载能力，即桩基承台效应。桩承台应采用钢筋混凝土材料，采用现场浇筑施工。承台的混凝土强度等级不低于C20。钢筋混凝土保护层厚度不应小于70mm，当有混凝土垫层时，不应小于50mm；且不应小于桩头嵌入承台内的长度。

桩基承台应满足抗冲切、抗剪切、抗弯承载力的要求。下面分别论述。

2.桩基承台的抗弯计算

抗弯计算实际上是配筋计算，多数承台的含钢量较低，常为受弯破坏，所以应按承台截面最大弯矩进行配筋。

柱下桩基承台的弯矩按以下简化计算方法确定。

（1）多桩矩形承台计算截面取在柱边和承台高度变化处（杯口外侧或台阶边缘，如图5.9-4a所示）

M_x=∑N_iy_i （5.9-8a）

M_y=∑N_ix_i （5.9-8b）

式中 M_x、M_y——垂直Y轴和X轴方向计算截面处的弯矩设计值（kN·m）；

x_i、y_i——垂直Y轴和X轴方向自桩轴线到相应计算截面的距离（m）；

N_i——扣除承台和其上填土自重后相应于作用的基本组合时的第i根桩竖向力设计值（kN）。

（2）三桩承台

1）等边三桩承台（如图5.9-4b所示）。

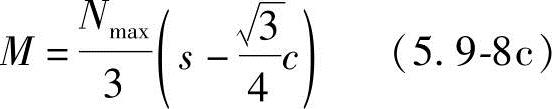
式中 M——由承台形心至承台边缘距离范围内板带的弯矩设计值（kN·m）；

N_max——扣除承台和其上填土自重后的三桩中相应于作用的基本组合时的最大单桩竖向力设计值（kN）；

s——桩距（m）；

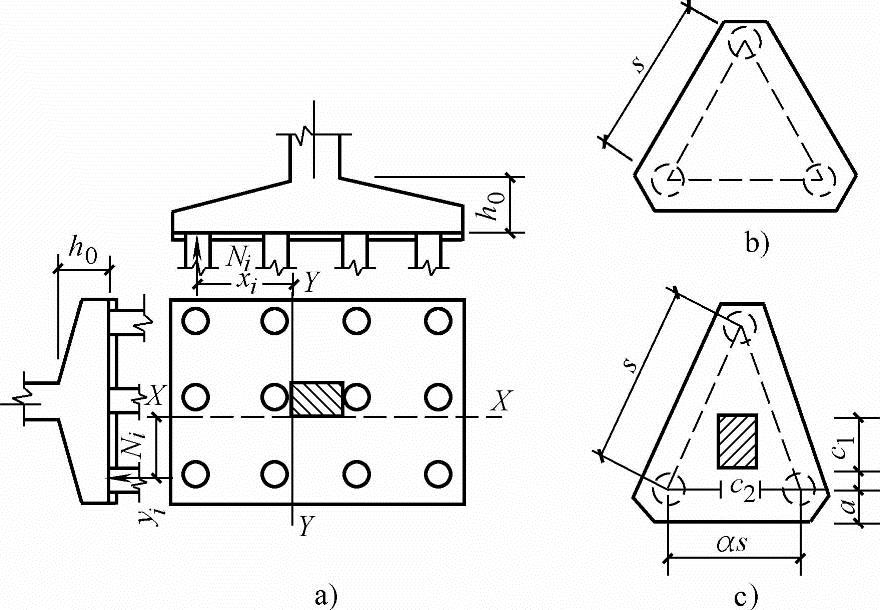
图5.9-4 承台弯矩计算图示

c——方柱边长（m），圆柱时c=0.866d（d为圆柱直径）。

2）等腰三桩承台（如图5.9-4c所示）。

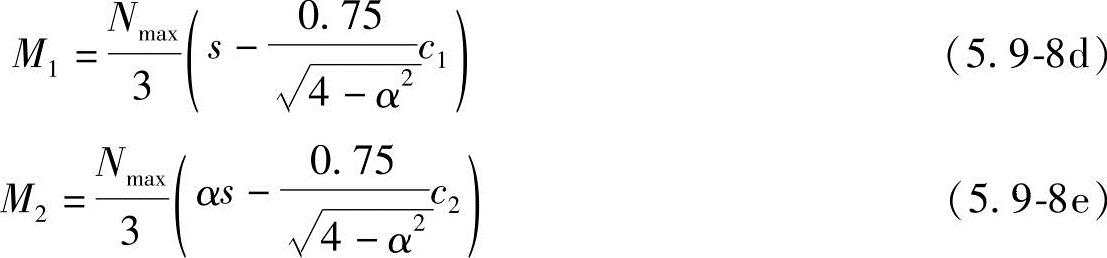
式中 M₁、M₂——由承台形心到承台两腰和底边的距离范围内板带的弯矩设计值（kN·m）；s——长向桩距（m）；

α——短向桩距与长向桩距之比，当α小于0.5时，应按变截面的二桩承台设计；

c₁、c₂——垂直于、平行于承台底边的柱截面边长（m）。

3.柱下桩基础独立承台的冲切计算

承台的冲切问题有两种：一种是柱对承台自上而下的冲切，另一种是桩顶竖向净反力对承台自下而上的冲切。

（1）柱对承台的冲切承台在承受柱传来的荷载时，若承台厚度不足，就会发生如图5.9-5所示的冲切破坏，在柱子的四周形成一个不大于45°的斜面冲切破坏锥体。对于矩形截面柱的矩形承台，在柱与承台交接处以及承台变阶处的冲切，可按下列公式计算（如图5.9-5所示）

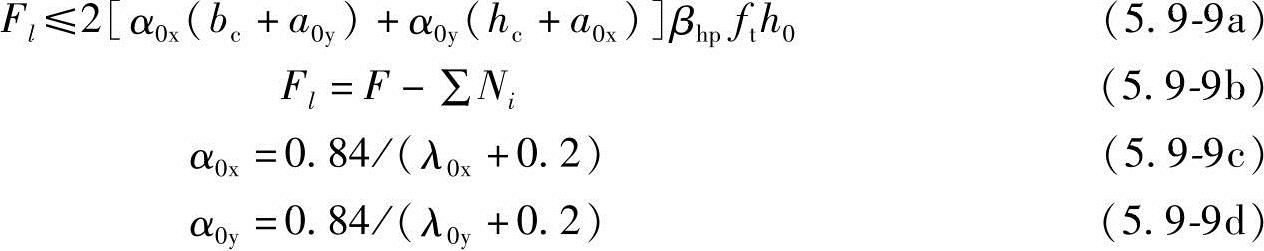
式中 F_l——扣除承台及其上填土自重，作用在冲切破坏锥体上相应于作用的基本组合时的冲切力设计值（kN），冲切破坏锥体应采用自柱边或承台变阶处至相应桩顶边缘连线构成的锥体，锥体与承台底面的夹角不小于45°，如图5.9-5所示；

h₀——冲切破坏锥体的有效高度（m）；

β_hp——受冲切承载力截面高度影响系数，当h不大于800mm时，β_hp取1.0；当h大于或等于2000mm时，β_hp取0.9，其间按线性内插法取用；

α_0x、α_0y——冲切系数；

λ_0x、λ_0y——冲跨比，λ_0x=a_0x/h₀，λ_0y=a_0y/h₀，a_0x、a_0y为柱边或变阶处至桩边的水平距离；当a_0x（a_0y）＜0.25h₀时，a_0x（a_0y）=0.25h₀；当a_0x（a_0y）＞h₀时，a_0x（a_0y）=h₀；

F——柱根部轴力设计值（kN）；

∑N_i——冲切破坏锥体范围内各桩的净反力设计值之和（kN）。

对中低压缩性土上的承台，当承台与地基土之间没有脱空现象时，可根据地区经验适当减小柱下桩基础独立承台受冲切计算的承台厚度。

对于圆柱和圆桩，计算时应将截面换算成方柱及方桩，即换算柱截面边宽b_c=0.886d_c，换算桩截面边宽b₀=0.8d₀，此处d_c和d₀分别为柱和桩的直径。

（2）角桩对承台的冲切当承台边缘处的厚度较小时，桩的反力有可能使承台边缘沿45°斜截面产生冲切破坏，如图5.9-6所示。此时承台板的抗冲切强度按《规范》规定计算。

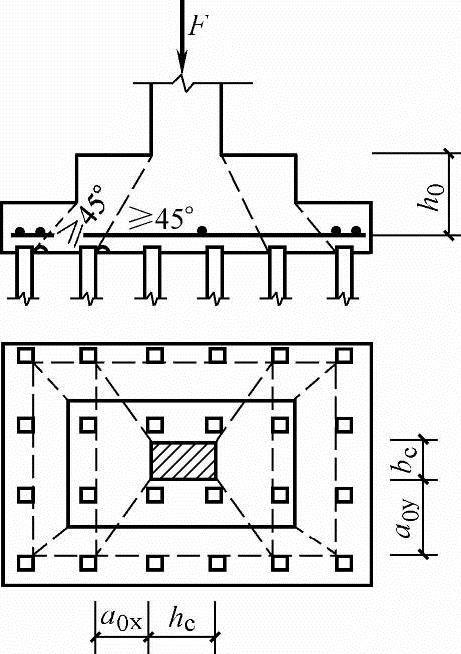
图5.9-5 柱对承台冲切计算图示

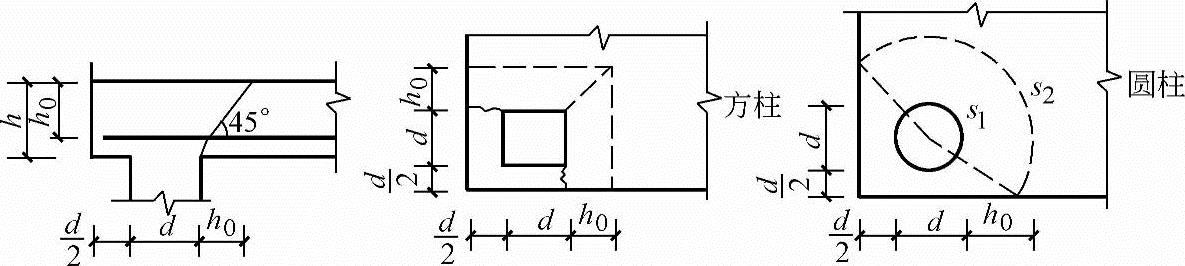
图5.9-6 角桩对承台冲切计算图示

1）多桩矩形承台受角桩冲切的承载力应按式（5.9-10a）计算（如图5.9-7所示）。

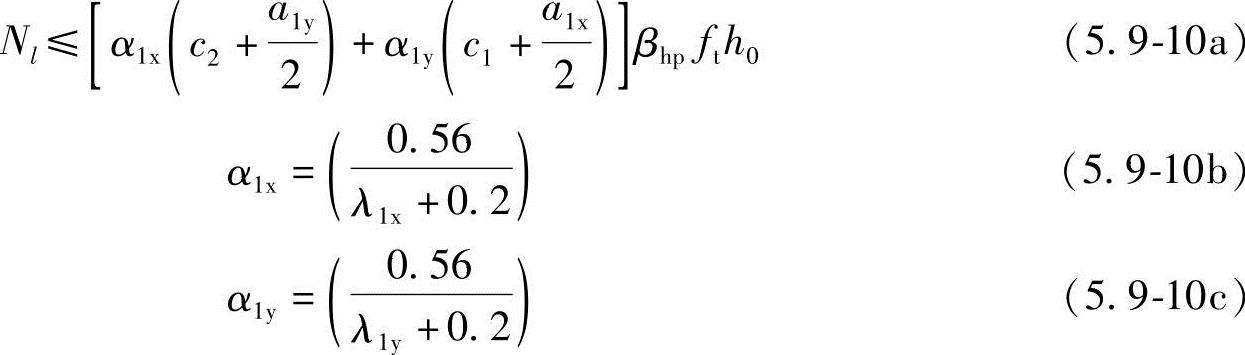
式中 N_l——扣除承台及其上填土自重后的角桩桩顶相应于作用的基本组合时的竖向力设计值；

α_1x、α_1y——角桩冲切系数；

λ_1x、λ_1y——角桩冲跨比，其值满足0.25～1.0，λ_1x=a_1x/h₀、λ_1y=a_1y/h₀；

c₁、c₂——从角桩内边缘至承台外边缘的距离（m）；

a_1x、a_1y——从承台底角桩内边缘引45°冲切线与承台顶面或承台变阶处相交点至角桩内边缘的水平距离（m）；

h₀——承台外边缘的有效高度（m）。

2）三桩三角形承台受角桩冲切的承载力可按下列公式计算（如图5.9-8所示）。

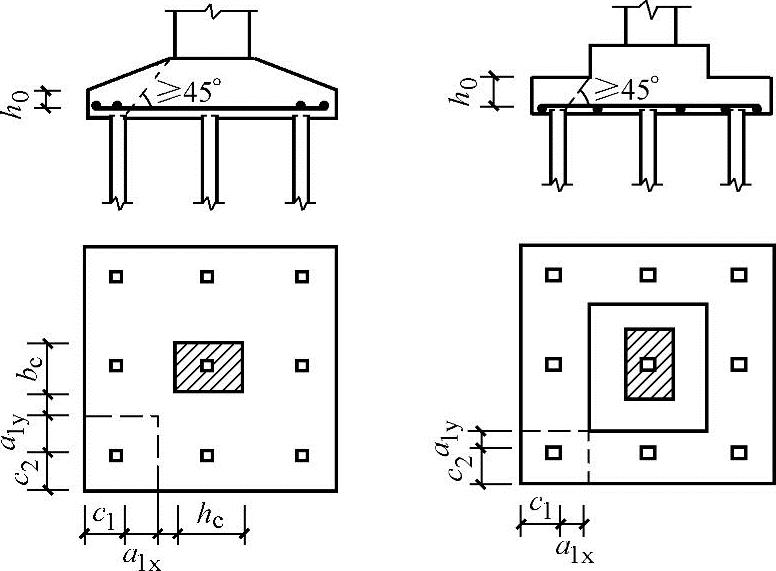
图5.9-7 矩形承台角桩冲切验算图示

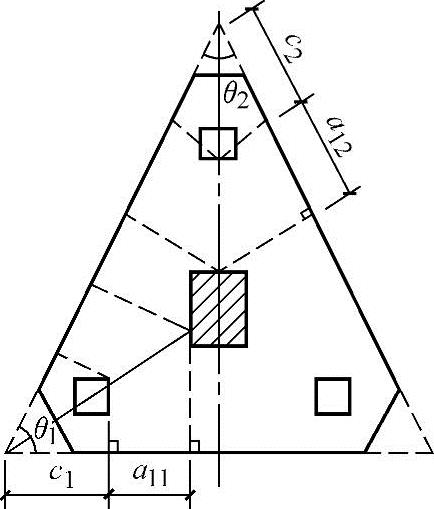
图5.9-8 三角形承台角桩冲切验算示意图

底部角桩

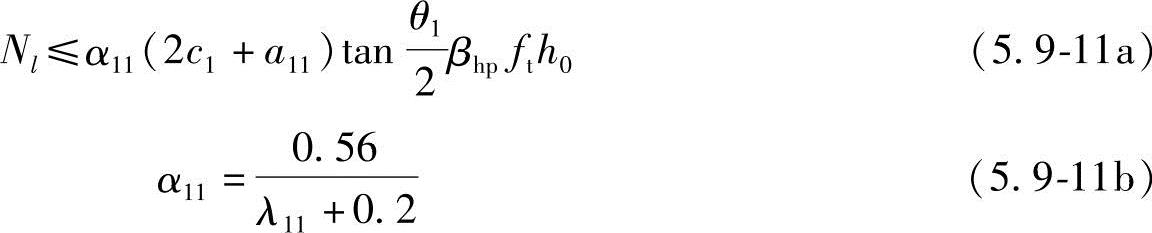
顶部角桩

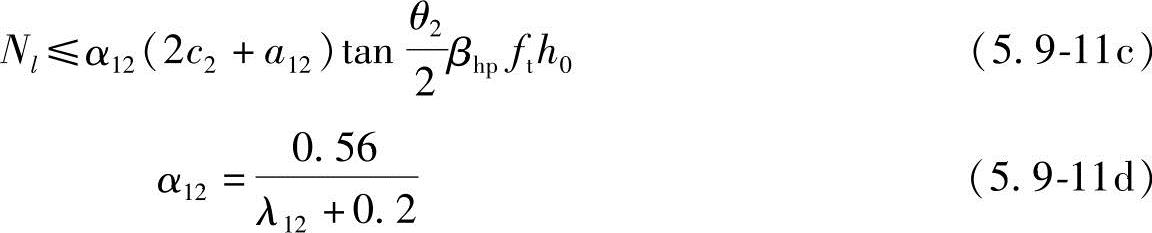
式中 λ₁₁、λ₁₂——角桩冲跨比，其值满足0.25～1.0，λ₁₁=a₁₁/h₀、λ₁₂=a₁₂/h₀；

a₁₁、a₁₂——从承台底角桩内边缘向相邻承台边引45°冲切线与承台顶面相交点至角桩内边缘的水平距离（m）；当柱位于该45°线以内时则取柱边与桩内边缘连线为冲切锥体的锥线。

对圆柱及圆桩，计算时可将圆形截面换算成正方形截面。

4.桩基承台的受剪计算

剪切破坏面为荷载作用处与支座间连线所形成的斜截面，即柱边（墙边）和桩边连线所形成的斜截面，应对柱的纵、横（x-x，y-y）两个方向的斜截面分别进行受剪承载力验算。

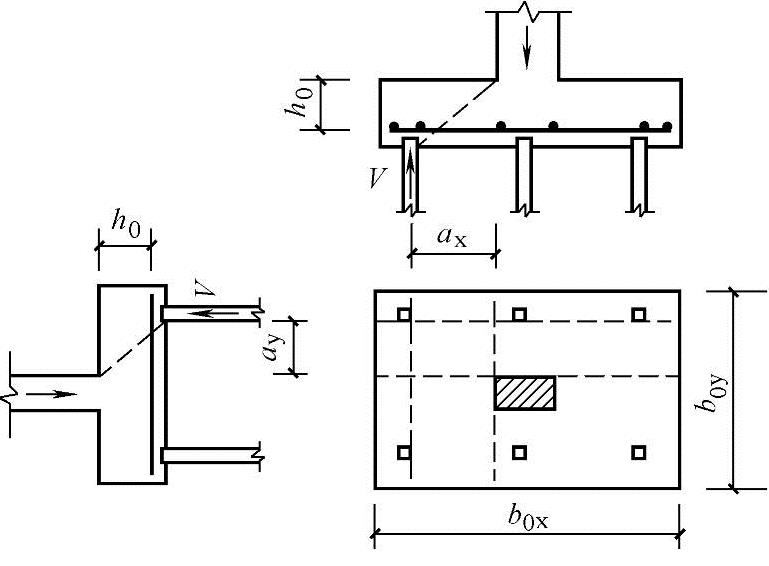
图5.9-9 承台斜截面受剪计算示意图

《规范》规定：柱下桩基础独立承台应分别对柱边和桩边、变阶处和桩边连线形成的斜截面进行受剪计算。当柱边外有多排桩形成多个剪切斜截面时，尚应对每个斜截面进行验算。

柱下桩基础独立承台斜截面受剪承载力可按下列公式计算（图5.9-9）

式中 V——扣除承台及其上填土自重后相应于作用的基本组合时的斜截面的最大剪力设计值（kN）；

b₀——承台计算截面处的计算宽度（m）；阶梯形承台变阶处的计算宽度、锥形承台的计算宽度应按《规范》附录U确定；

h₀——计算宽度处的承台有效高度（m）；

β——剪切系数；

β_hs——受剪切承载力截面高度影响系数，按β_hs=（800/h₀）1/4计算；

λ——计算截面的剪跨比，λ_x=a_x/h₀、λ_y=a_y/h₀；a_x、a_y为柱边或承台变阶处至x、y方向计算一排桩的桩边的水平距离，当λ＜0.25时，取λ=0.25；当λ＞3时，取λ=3。

《规范》附录U中阶梯形承台及锥形承台斜截面受剪的截面宽度计算方法摘录如下。

对于阶梯形承台应分别在变阶处（A₁—A₁、B₁—B₁）及柱边处（A₂—A₂、B₂—B₂）进行斜截面受剪计算，如图5.9-10所示。

图5.9-10 阶梯形承台斜截面受剪计算示意图

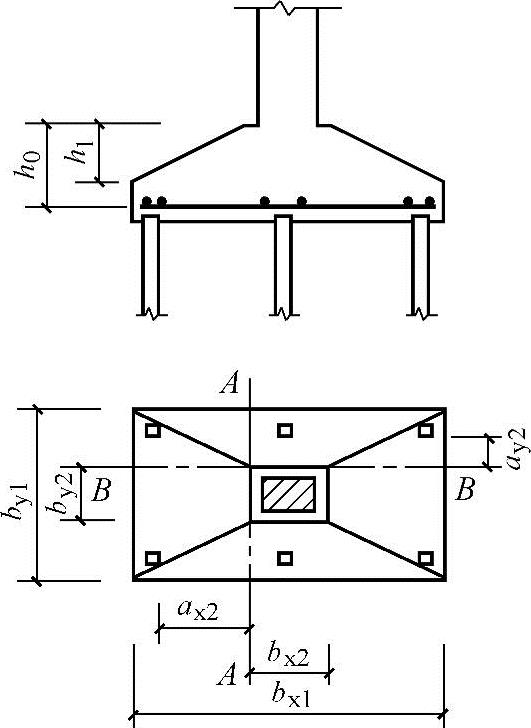
图5.9-11 锥形承台受剪计算示意图

计算变阶处截面A₁—A₁、B₁—B₁的斜截面受剪承载力时，其截面有效高度均为h₀₁，截面计算宽度分别为b_y1和b_x1。

计算柱边截面A₂—A₂和B₂—B₂处的斜截面受剪承载力时，其截面有效高度均为h₀₁+h₀₂，截面计算宽度按下式计算。

对A₂—A₂

对B₂—B₂

对于锥形承台应对A—A及B—B两个截面进行受剪承载力计算，如图5.9-11所示，截面有效高度均为h₀，截面的计算宽度按下式计算。

对A—A

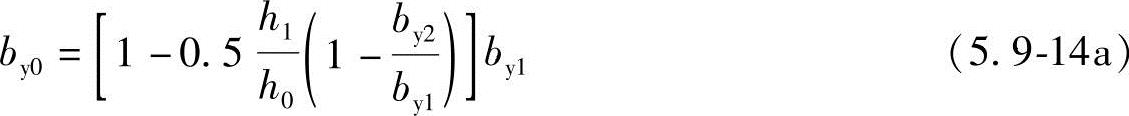
对B—B

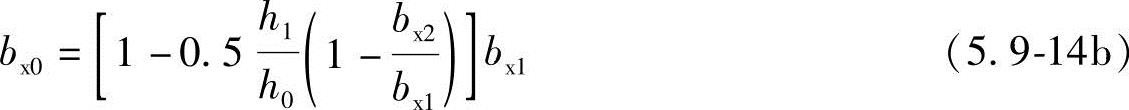
【例5.9-10】～【例5.9-14】有一等边三桩承台基础，采用沉管灌注桩，桩径为426mm，有效桩长为24m。有关地基各层土层分布情况、桩端阻力特征值、桩侧阻力特征值及桩的布置、承台尺寸等如图5.9-12所示。

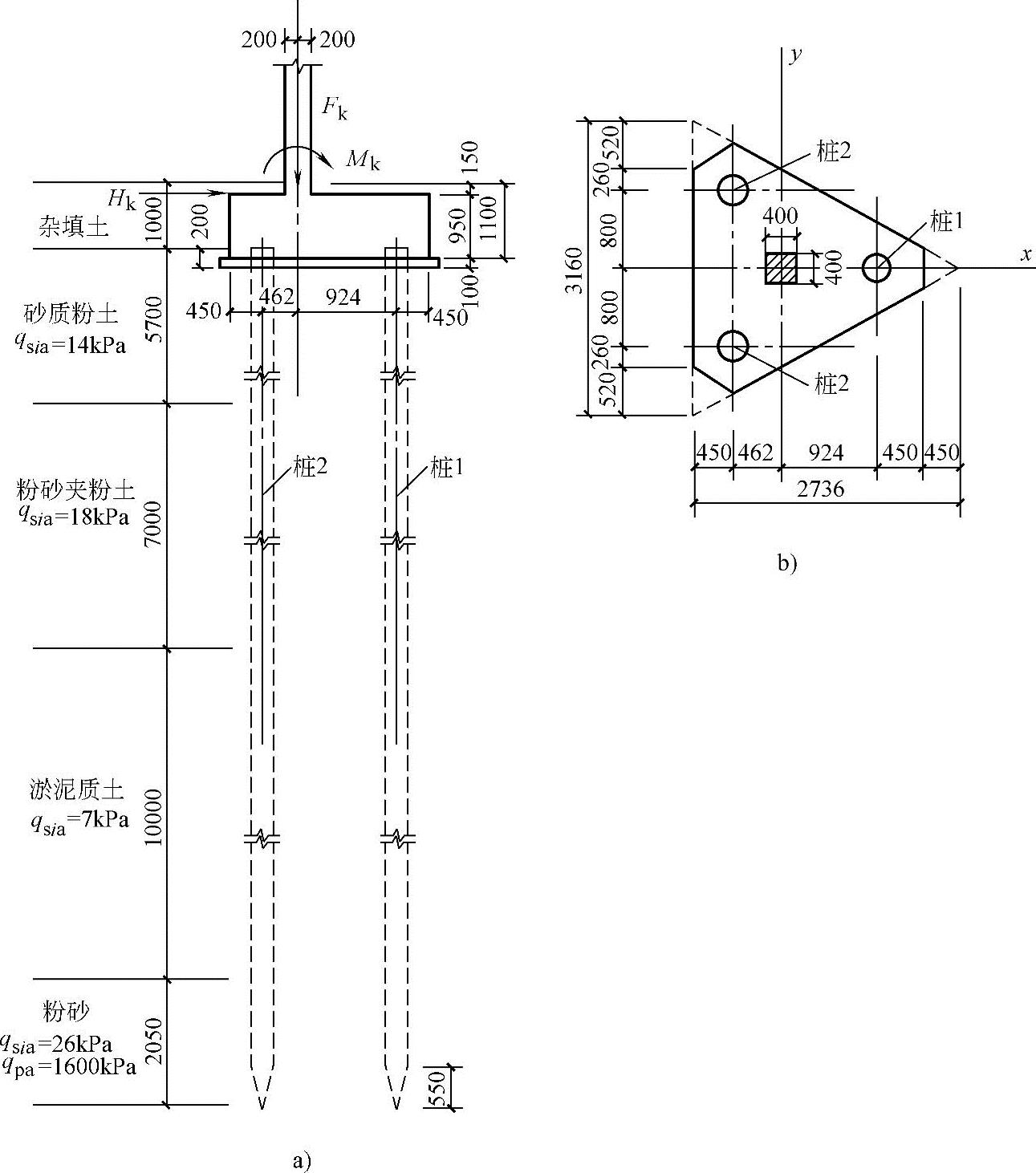
图5.9-12 【例5.9-10】～【例5.9-14】图

【例5.9-10】按《规范》的规定，在初步设计时，估算该桩基础的单桩竖向承载力特征值R_a（kN），并指出其值最接近下列哪项数值？

（A）361 （B）645 （C）665 （D）950

答案：（B）

解答：采用经验参数法进行计算，利用式（5.9-1）

R_a=q_paA_p+up∑q_sial_i

其中桩身周边长度u_p=dπ=0.426πm=1.338m

桩底端横截面面积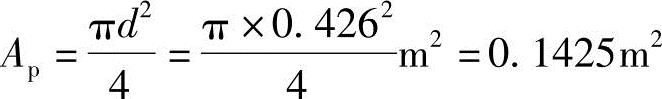

R_a=q_paA_p+u_p∑q_sial_i

=[1600×0.1425+1.338×（14×5.5+18×7.0+7×10+26×1.5）]kN

=[228.00+1.338×（77+126+70+39）]kN=（228.00+1.338×312）kN

=（228.00+417.46）kN=645.46kN

【例5.9-11】假定钢筋混凝土柱传至承台顶面处的标准组合值为竖向力F_k=1400kN，力矩M_k=160kN·m，水平力H_k=45kN；承台自重及承台上土自重标准值G_k=87.34kN。在上述一组力的作用下，试问桩1桩顶竖向力Q_k（kN）最接近下列哪项数值？

（A）590 （B）610 （C）620 （D）640

答案：（D）

解答：已知G_k=87.34kN

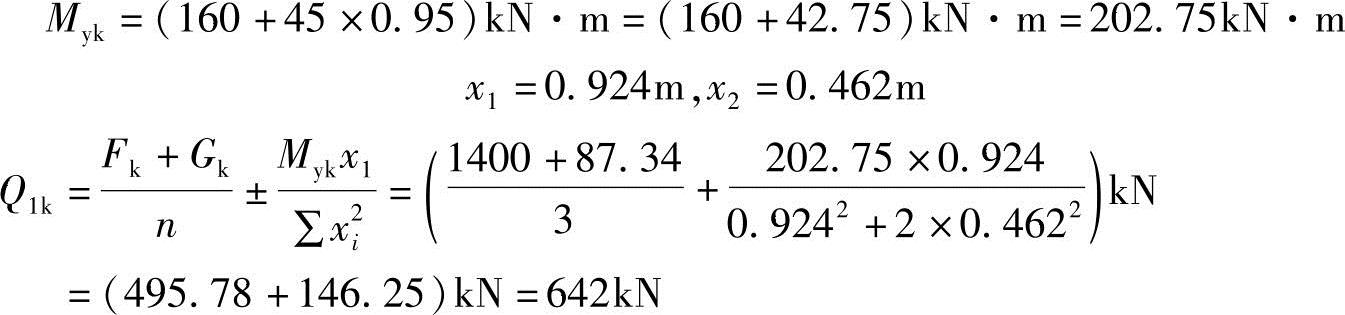
【例5.9-12】假定由柱传至承台的作用由永久作用控制，承台自重和承台上的土重G_k=87.34kN；在标准组合偏心竖向力作用下，最大单桩（桩1）竖向力Q_1k=610kN。试问，由承台形心到承台边缘（两腰）距离范围内板带的弯矩设计值M₁（kN·m）最接近下列哪项数值？

（A）276 （B）336 （C）376 （D）392

答案：（C）解答：为等边三桩承台，按照式（5.9-8c）计算弯矩。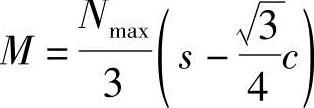

其中，扣除承台和其上填土自重后的三桩中相应于作用的基本组合时的最大单桩竖向力设计值N_max计算如下

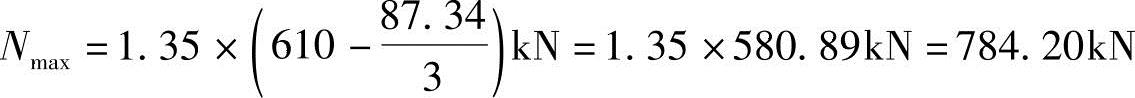
式中的系数1.35为由作用的标准组合值换算为作用的基本组合的设计值时的系数，桩距s=1.60m，方桩边长由圆桩直径换算，c=0.866d=0.866×0.426=0.369m。

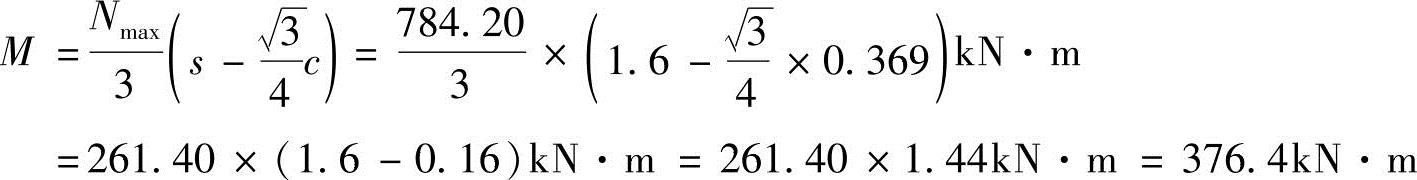
【例5.9-13】已知c₂=939mm，a₁₂=467mm，h₀=890mm，角桩冲跨比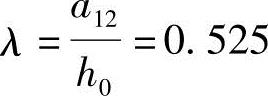；承台采用混凝土强度等级C25。试问，承台受桩1冲切的承载力（kN）最接近下列哪项数值？

（A）740 （B）810 （C）850 （D）1166

答案：（D）

解答：桩1为顶部角桩，确定顶部角桩对承台的冲切，采用式（5.9-11c）右端公式计算。

其中，已知角桩冲跨比

λ₁₂=a₁₂/h₀=467/890=0.525

角桩冲切系数

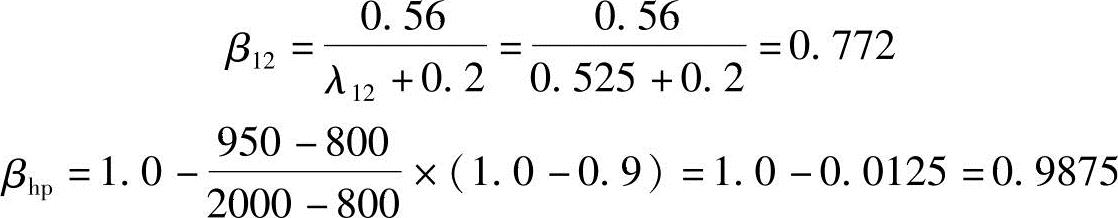
混凝土强度等级为C25，f_t=1.27MPa，等边三角形θ₂=60°

承台受角桩冲切的承载力为

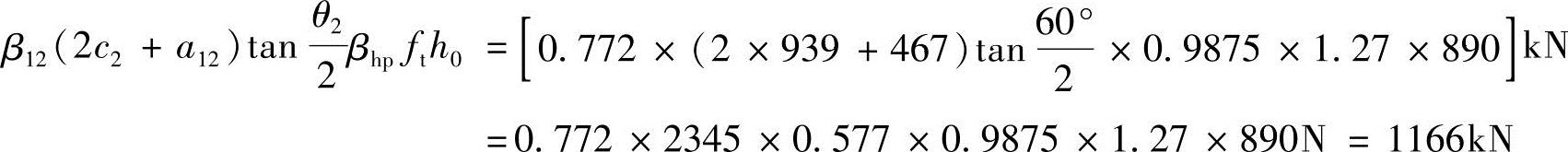
【例5.9-14】已知b₀=2427mm，h₀=890mm，剪跨比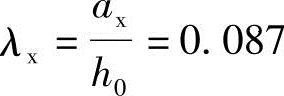；承台采用混凝土强度等级C25。试问，承台对底部角桩（桩2）形成的斜截面受剪承载力（kN）最接近于下列哪项数值？

（A）2990 （B）3460 （C）3740 （D）4140

答案：（C）

解答：斜截面受剪承载力采用式（5.9-12a）右端β_hsβf_tb₀h₀公式计算。

已知计算截面的剪跨比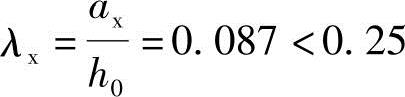：，取λ_x=0.25。

剪切系数

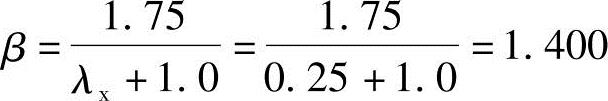
受剪切承载力截面高度影响系数，按。

承台对底部角桩（桩2）形成的斜截面受剪承载力为

β_hsβf_tb₀h₀=0.974×1.400×1.27×2427×890N=3740679N=3741kN

5.桩基承台局部受压计算

《规范》规定：当承台的混凝土强度等级低于柱或桩的混凝土强度等级时，尚应验算柱下或桩上承台的局部受压承载力。具体计算公式见《混凝土结构设计规范》。

5.9.5桩基承台设计与计算方法

相关推荐