图5-19三维角色的多角度造型5.3.4头部的设计一个角色设计得好坏在很大程度上取决于角色头部的设计。无论是人物角色还是动物角色，五官与头部基本形的处理都是设计的根本任务。......
2025-09-29
钢筋混凝土联合基础设计教程
【摘要】：采用静力分析方法计算基础内力，即截面弯矩和剪力设计值，并绘出分布图。 假定作用的基本组合竖向力F1=1100kN，F2=900kN，右边支座悬挑尺寸b=1000mm，则基础梁左边支座悬挑尺寸c为下列哪项数值时，地基反力才呈均匀（矩形）分布状态？图5.8-11 ～用图1100mm 1200mm 1300mm 1400mm答案：解答：先确定基础长度L。 条件同，其基础梁最大剪力设计值与下列哪项数值最接近？
当两个柱下独立基础距离较近，或由于场地条件限制，其中一个柱下独立基础边缘扩展受限，往往设计成双柱下联合基础，按照联合基础底面形状可分为矩形联合基础和梯形联合基础。
联合基础的设计包括：确定联合基础底面尺寸；按照基底净反力设计值计算基础内力，即截面弯矩和剪力；再根据受剪和受冲切承载力确定基础底板厚度；根据最大弯矩确定基础底板的纵向配筋。具体计算设计步骤如下：
（1）计算柱荷载的合力作用位置，确定外荷载作用重心。
（2）确定基础长度l，确定依据是使基础底面形心尽可能与柱荷载重心重合。
（3）按照满足地基承载力要求确定基础底面宽度b。
（4）假定基底反力线性分布计算基底净反力设计值。
（5）采用静力分析方法计算基础内力，即截面弯矩和剪力设计值，并绘出分布图。
（6）根据受剪承载力和受冲切承载力确定基础高度，一般可先假定基础高度，再进行高度验算：
1）受剪承载力验算。
验算公式可根据墙下条形基础的受剪承载力验算式（5.8-7）进行改变
V≤0.7βhpftbh0 （5.8-23）
2）受冲切承载力验算。
验算公式可直接采用柱下独立基础的受冲切承载力验算公式（5.8-17a）。
（7）由弯矩图中的最大正负弯矩按照前述公式进行纵向配筋计算。
【例5.8-35】～【例5.8-40】 某双柱下条形基础梁，荷载效应作用的基本组合条件下，由柱传至基础梁顶面的上部结构竖向力分别为F1和F2。基础梁尺寸及工程地质剖面如图5.8-11所示。假定基础梁为无限刚度，地基反力可按直线分布考虑。
【例5.8-35】 假定作用的基本组合竖向力F1=1100kN，F2=900kN，右边支座悬挑尺寸b=1000mm，则基础梁左边支座悬挑尺寸c为下列哪项数值时，地基反力才呈均匀（矩形）分布状态？
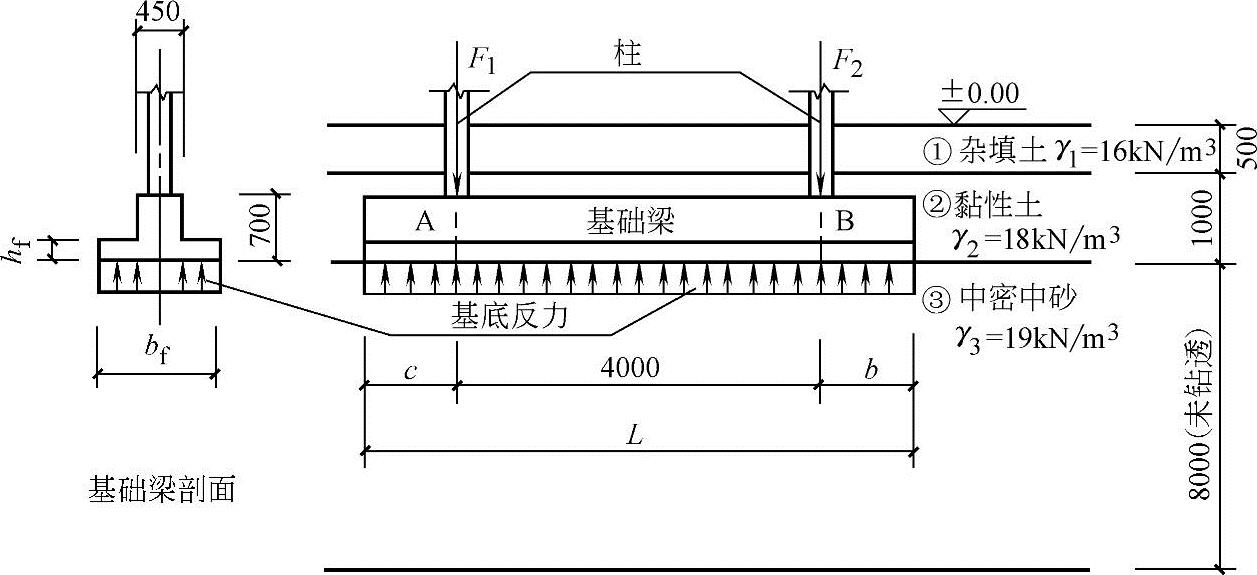
图5.8-11 【例5.8-35】～【例5.8-40】用图（尺寸单位：mm）
（A）1100mm （B）1200mm （C）1300mm （D）1400mm
答案：（D）
解答：先确定基础长度L。
总竖向外荷载设计值
∑F=F1+F2=（1100+900）kN=2000kN
设合力作用点距左边柱中点A的距离为x，以A为矩心，有2000x=4000F2=4000×900，则合力重心距A点x=1800mm。
则距右边柱B点的距离为（4000-1800）mm=2200mm。
若使得总外荷载通过矩形基底的中点，以便使基底反力均匀分布，则基础长度L应为
L=2×（2200+b）=2×（2200+1000）mm=6400mm
L=4000+1000+c，故c=1400mm
【例5.8-36】 已知基础梁翼板宽度bf=1250mm，中密中砂层地基承载力特征值fak=250kPa。则地基承载力修正后的特征值fa与下列哪项数值最接近？
（A）278kPa （B）287kPa （C）302kPa （D）326kPa
答案：（D）
解答：查表5.6-1确定中砂承载力系数ηb=3.0，ηd=4.4，bf=1250mm＜3m，取为3m。
【例5.8-37】 假定正常使用极限状态下作用的标准组合Fk1=1206kN，Fk2=804kN，c=1800mm，b=1000mm，地基承载力修正后特征值fa=300kPa，计算基础梁自重与上覆填土自重的平均重度γG=20kN/m3，地基反力可按均匀分布考虑。则基础梁翼板的最小宽度bfmin与下列哪项数值最接近？
（A）1000mm （B）1100mm （C）1200mm （D）1300mm
答案：（B）
解答：此时基础长度
【例5.8-38】 假定作用的基本组合F1=1206kN，F2=804kN，c=1800mm，b=1000mm。当柱支座宽度的影响略去不计时，其基础梁支座处最大弯矩设计值与下列哪项数值最接近？
（A）147.8kN·m （B）123.2kN·m （C）478.9kN·m （D）399.1kN·m
答案：（C）
解答：基础纵向每米长度的总净反力，即为单位面积上的净反力与基础宽度的乘积
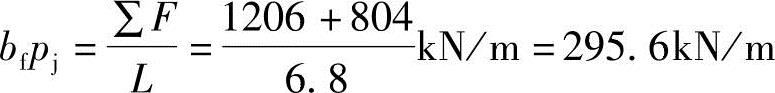
A支座距左边缘的距离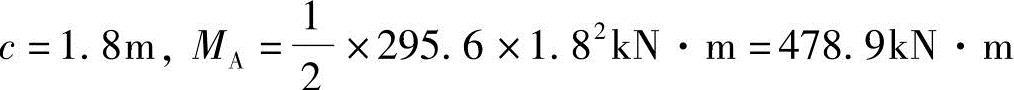
；B支座距右边缘的距离b=1.0m，
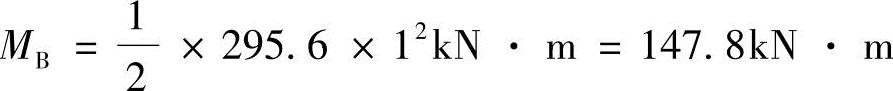，Mmax=MA=478.9kN·m。
【例5.8-39】 条件同【例5.8-38】，其基础梁最大剪力设计值与下列哪项数值最接近？
（A）673.95kN （B）591.18kN （C）561.63kN （D）493.03kN
答案：（A）
解答：最大剪力在A支座右侧
VA=（295.6×1.8-1206）kN=-673.92kN
【例5.8-40】 条件同【例5.8-38】，其基础梁的跨中最大弯矩设计值与下列哪项数值最接近？
（A）205.85kN·m （B）231.56kN·m （C）289.45kN·m （D）519.18kN·m
答案：（C）
解答：设最大弯矩截面与基础左侧A点的距离为x0，由该截面剪力为零的条件可得
295.6（1.8+x0）-1206=0，x0=（4.08-1.8）m=2.28m
最大弯矩设计值
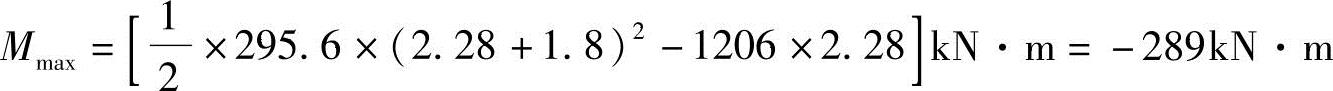
【例5.8-41】～【例5.8-47】 设计如图5.8-12所示的二柱矩形联合基础。基础材料是：混凝土C20，HRB335钢筋。已知柱1、柱2截面为bc×hc=300mm×300mm。要求基础左侧与柱1外侧对齐，已知基础埋深为1.50m，基础宽度b=1000mm，高h=500mm，荷载效应基本组合时，柱上作用有竖向力F1、F2，弯矩M1、M2。
(https://www.chuimin.cn)
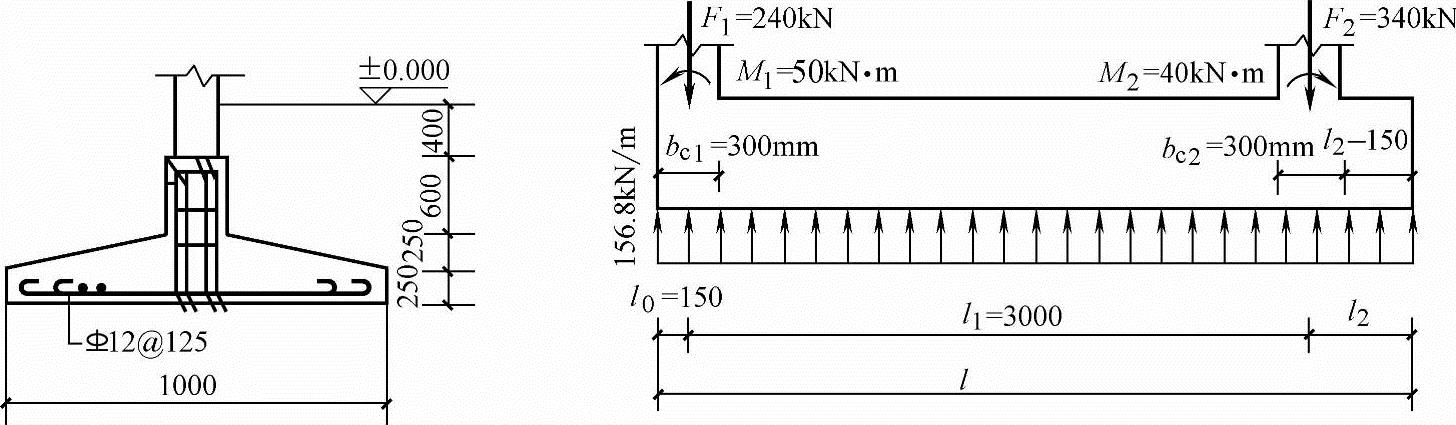
图5.8-12 【例5.8-41】～【例5.8-47】用图
【例5.8-41】 如果题中F1=240kN，F2=340kN，M1=50kN·m，M2=40kN·m，当基底反力均匀分布时，柱2轴心距联合基础右端距离l2与下列哪项数值最接近？
（A）540mm （B）580mm （C）630mm （D）670mm
答案：（C）
解答：先确定基础长度l
总竖向外荷载
∑F=F1+F2=（240+340）kN=580kN
设合力作用点距左边柱1轴心的距离为x，以左边柱轴心为矩心，有580x+M1-M2=3.0F2=3.0×340=1020，则合力重心距柱1轴心距离为
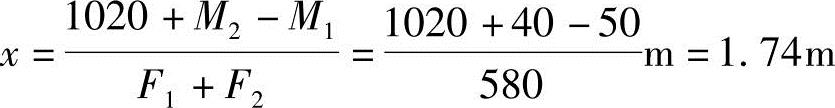
若使得总外荷载通过矩形基底的中点，以便使基底反力均匀分布，则基础长度l应为2×（1.74+bc1/2）=2×（1.74+0.15）m=3.78m。
由l=0.15+3.0+l2=3.78m，故l2=0.63m=630mm。
【例5.8-42】 如F1=240kN，F2=340kN，M1=50kN·m，M2=40kN·m不变，l=3700mm，l2=550mm时，柱1轴线右侧剪力与下列哪项数值最接近？
（A）-225.8kN （B）-216.5kN （C）-201.5kN （D）-190.3kN
答案：（B）
解答：基础纵向每米长度的总净反力，即为单位面积上的净反力与基础宽度的乘积
【例5.8-43】 如条件同【例5.8-42】时，柱2轴线左侧剪力与下列哪项数值最接近？
（A）-253.76kN （B）-260.94kN （C）-265.49kN （D）-270.89kN
答案：（A）
解答：V2左=（156.8×0.55-340）kN=-253.76kN
【例5.8-44】 如条件同【例5.8-42】时，基础最大弯矩设计值与下列哪项数值最接近？
（A）-176.9kN·m （B）-180.84kN·m （C）-186.42kN·m （D）-192.6kN·m
答案：（D）
解答：设最大弯矩截面与基础左侧端点的距离为x0，由该截面剪力为零的条件可得
156.8x0-240=0，x0=（240/156.8）m=1.53m
最大弯矩设计值为
【例5.8-45】 如条件同【例5.8-42】，进行冲切验算时，柱1内侧面的冲切力设计值与下列哪项数值最接近？
（A）110.6kN （B）122.4kN （C）135.6kN （D）139.8kN
答案：（B）
解答：考虑柱对基础的冲切验算。
基础有效高度为
h0=（500-50）mm=450mm=0.45m
冲切破坏锥体的底边长为
bc1+2h0=（0.3+2×0.45）m=1.2m＞b=1.0m
表明冲切破坏锥体底面落在基础宽度以外，如图5.8-13虚线所示。
先计算冲切破坏锥体实际的底面积，对柱1
Al1=（bc1+h0）b=[（0.3+0.45）×1.0]m2
=0.75m2
冲切力设计值
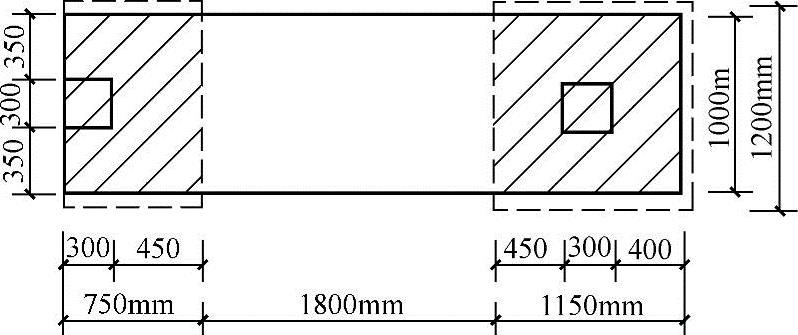
图5.8-13 【例5.8-45】～【例5.8-47】图示
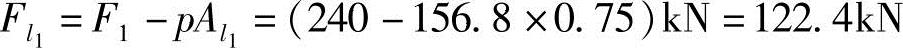
【例5.8-46】 如条件同【例5.8-42】，进行冲切验算时，柱2内侧面的冲切力设计值与下列哪项数值最接近？
（A）122.4kN （B）135.6kN （C）149.8kN （D）159.7kN
答案：（D）
解答：对柱2冲切破坏锥体实际的底面积，如图5.8-13所示。
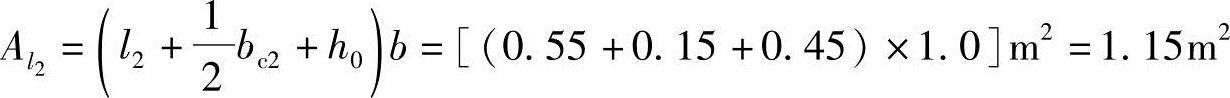
冲切力设计值
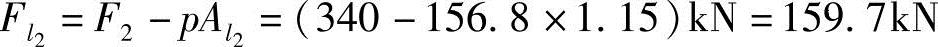
【例5.8-47】 如条件同【例5.8-42】，柱对基础的受冲切承载力（kN）与下列哪项数值最接近？
（A）215 （B）225 （C）235 （D）245
答案：（B）
解答：at+2h0=（0.3+2×0.45）m=1.2m＞1.0m，取ab=1.0m。
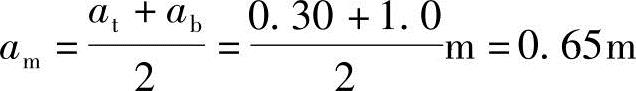
受冲切承载力
0.7βhpftamh0=0.7×1.0×1.10×103×0.65×0.45kN=225kN
相关文章
- 详细阅读
-
优化场景设计原则｜动画基础案例教程详细阅读
场景设计中的任何问题都是围绕着它的基本概念展开的。而场景设计是指动漫游戏中除角色造型以外的环境空间设计。图6-1游戏《三国志》场景社会环境性如《再见萤火虫》中的场景表现了战乱时期日本社会环境。图6-4电影《阿凡达》场景6.1.2 场景设计的意义作用1.场景存在的最基本意义——交代时空关系场景设计在游戏、动画影片中提供了角色表演的特定时间与空间的舞台。......
2025-09-29
-
无筋扩展基础设计-5.8.2简明教程详细阅读
无筋扩展基础的特点是基础的抗压性能较好而抗拉和抗剪性能较差。表5.8-6 无筋扩展基础台阶宽高比的允许值注：1.pk为作用的标准组合时基础底面处的平均压力值。因为计算基础宽度不超过3m，所以不需要再进行地基承载力特征值的宽度修正。......
2025-09-30
-
动画基础案例教程：前期创作与角色设计详细阅读
前期创作的人员是团队的核心成员，参与人员一般不会太多，这一阶段的工作往往会交替进行，反复修改和讨论。图3-2文字分镜头《生活原来是这样的》图3-3《僵尸新娘》体现了蒂姆·伯顿独特的美术风格5.角色造型设计角色是给观众感受最为直接的动画元素，许多动画影片的主要目的就是塑造角色。......
2025-09-29
-
动画基础原理-动画基础案例教程详细阅读
“动画”的中文叫法源自日本。第二次世界大战前后，日本称用线条描绘的漫画作品为“动画”。随着新技术的应用，动画片的界定也变得复杂了。确切地讲，动画片属于视听艺术范畴。“视觉暂留”理论成为动画与电影的基石，也加速了动画与影视的发展。......
2025-09-29
-
Modelsim基础教程详细阅读
图5.23 编译图5.24 编译完成3.启动仿真工具当设计文件“traffic_lights_state_machine.v”和测试文件“testbench.v”编译通过之后，启动仿真工具。图5.27中，弹出时默认选中第一个“No design object visibility”，需要改选为第二个“Apply full visibility to all modules”选项，第二个选项可以使模块内部及模块连接间的信号都能被观察到，能够帮助我们更好地进行调试，而其他选项只能看到部分信号。......
2025-09-29
-
传统动画制作教程-动画基础案例教程详细阅读
图9-5动画定位尺图9-6打孔机9.1.5拷贝台拷贝台又叫透写台、透光台、临摹台，是制作漫画、动画时的专业工具。拷贝台是动画师和漫画师必不可少的工具之一。图9-7拷贝台9.1.6动画桌动画桌也称透光桌、拷贝桌。图9-9赛璐珞片9.1.8动画规格框规格框也称安全框，是动画纸上的画面外延尺寸的边框，在框内所作的画才是有效的。......
2025-09-29
-
动物造型设计的卡通化-动画基础案例教程详细阅读
图5-34动画《战鸽飞翔》图5-35动画《马达加斯加2》5.4.1动物造型设计的卡通化使用概括的造型手段来塑造动物卡通角色的形象是卡通式造型的重要表现手法。图5-37以几何形体为基础来丰富角色细节5.4.3常见的卡通动物造型1.兽类在众多的兽类动物中，可以大致分为两大类：爪类和蹄类。图5-40家禽动物卡通造型图5-41鸟类角色造型4.两栖类和爬行类两栖类动物是指既能在陆地上活动，又能在水中活动的一类动物，比如青蛙。......
2025-09-29
相关推荐