朗肯土压力理论学习笔记

1.主动土压力计算

对无黏性土

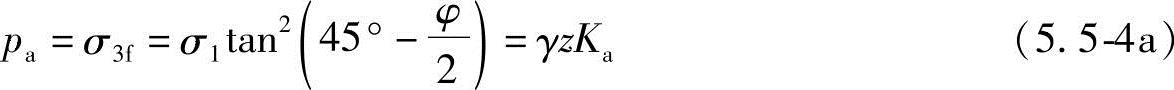
对黏性土

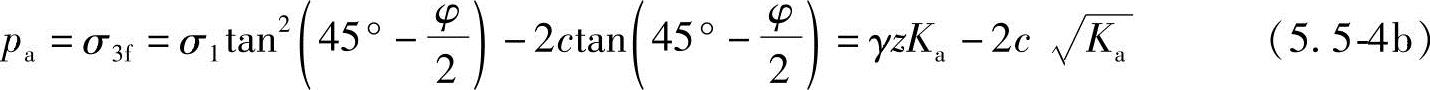
式中 γ——土的重度（kN/m³）；

z——计算点距填土表面的距离（m）；

K_a——主动土压力系数，；

φ——内摩擦角（°）；

c——黏聚力（kPa）。

由式（5.5-4a）和式（5.5-4b）分别可得到无黏性土和黏性土的主动土压力的强度分布，如图5.5-2b、c所示。

图5.5-2 朗肯主动土压力分布

总主动土压力可由分布图的面积求得（略去负值）。

无黏性土

黏性土

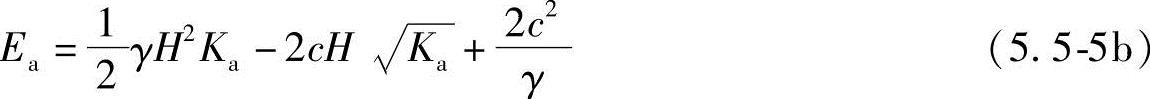
总主动土压力作用方向垂直指向墙背，作用点通过分布图的形心，如图5.5-2b、c所示。

2.被动土压力计算

对无黏性土可由式（5.5-6a）计算

对黏性土

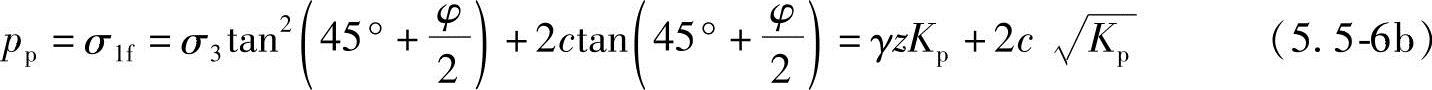
式中 K_p——被动土压力系数，。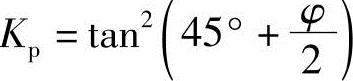

其他符号同前。

无黏性土和黏性土的被动土压力的分布分别如图5.5-3b、c所示。

总被动土压力可由分布图的面积求得。

无黏性土

黏性土

总被动土压力作用方向垂直指向墙背，作用点通过分布图的形心，如图5.5-3b、c所示。

【例5.5-1】～【例5.5-3】 某挡土墙高5m，墙背垂直、光滑，填土表面水平。填土重度γ=18kN/m³，内摩擦角φ=40°，黏聚力c=0。

【例5.5-1】 试问静止土压力合力大小和作用点距墙底位置与下列哪组数值最接近？

（A）19.53kN/m，1.67m

（B）48.83kN/m，1.67m

（C）32.13kN/m，1.67m

（D）80.33kN/m，1.67m

答案：（D）

解答：静止土压力系数

图5.5-3 朗肯被动土压力分布

K₀=1-sinφ′=1-sin40°=0.357

在墙顶

z=0，p₀=0

在墙底

z=H=5m，p₀=γzK₀=18×5×0.357kPa=32.13kPa

静止土压力合力为三角形分布图的面积

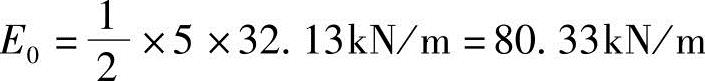
作用点：距墙底h/3=（5/3）m=1.67m。

【例5.5-2】 试问主动土压力合力大小和作用点距墙底位置与下列哪组数值最接近？

（A）19.53kN/m，1.67m （B）48.83kN/m，1.67m

（C）32.13kN/m，1.67m （D）80.33kN/m，1.67m

答案：（B）

解答：主动土压力系数

在墙顶

z=0，p_a=0

在墙底

z=H=5m，p_a=γzK_a=18×5×0.217kPa=19.53kPa

主动土压力合力

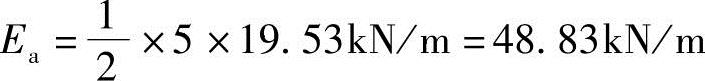
作用点：距墙底h/3=（5/3）m=1.67m。

【例5.5-3】 试问被动土压力合力大小和作用点距墙底位置与下列哪组数值最接近？

（A）19.5kN/m，1.67m （B）48.8kN/m，1.67m

（C）413.9kN/m，1.67m （D）1034.8kN/m，1.67m

答案：（D）

解答：被动土压力系数

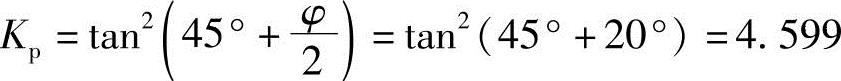
在墙顶

z=0，p_p=0

在墙底

z=H=5m，p_p=γzK_p=18×5×4.599kPa=413.91kPa

被动土压力合力

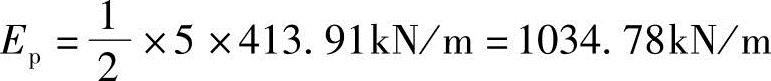
作用点：距墙底h/3=5m/3=1.67m。

【例5.5-4】～【例5.5-7】 某挡土墙高10m，如图5.5-4所示，墙背垂直、光滑，填土表面水平。填土重度γ=17.5kN/m³，内摩擦角φ=20°，黏聚力c=12kPa。（主动土压力增大系数取1.0）

【例5.5-4】 试问主动土压力系数与下列哪项数值最接近？

（A）0.49 （B）0.7

（C）1.43 （D）2.04

答案：（A）

解答：主动土压力系数

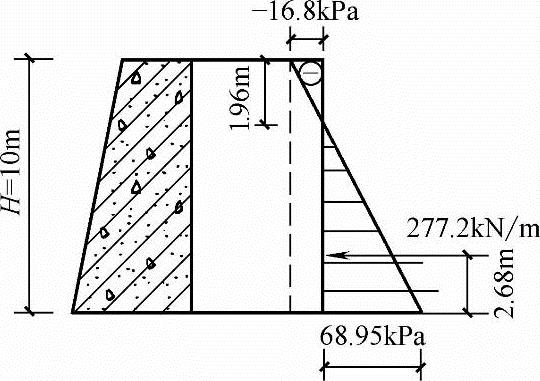
图5.5-4 【例5.5-4】～【例5.5-7】图及结果

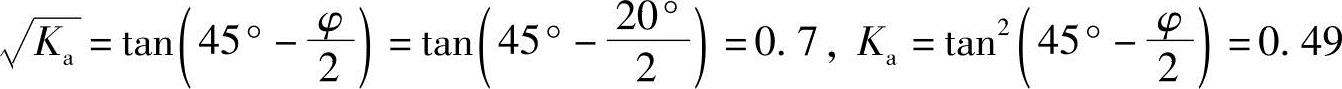
【例5.5-5】 试问墙底主动土压力强度数值与下列哪项数值最接近？

（A）-16.8kPa （B）69kPa （C）-16.8kN/m （D）69kN/m

答案：（B）

解答：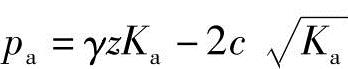

在墙顶

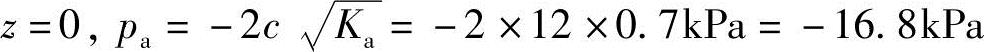
在墙底：z=H=10m p_a=（17.5×10×0.49-2×12×0.7）kPa=68.95kPa

绘出分布图如图5.5-4所示。

【例5.5-6】 试问墙顶受拉区深度与下列哪项数值最接近？

（A）0.96m （B）1.24m （C）1.45m （D）1.96m

答案：（D）

解答：受拉区深度由下述方法求得

则

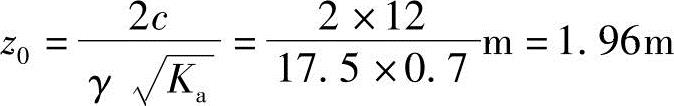
【例5.5-7】 试问总主动土压力合力大小和距墙底的位置与下列哪组数值最接近？

（A）260.7kPa，3.33m （B）277.2kPa，2.68m

（C）277.2kN/m，2.68m （D）260.7kN/m，3.33m

答案：（C）

解答：总主动土压力计算：

负值部分忽略。

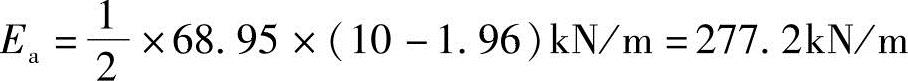
作用点：距墙底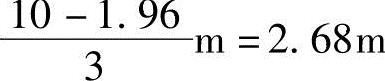，方向垂直指向墙背。

3.实际工程中朗肯土压力理论的应用

（1）水平填土表面作用均布荷载q 图5.5-5为墙后填土表面水平并作用均布荷载q的情况。此时深度z处微元体的水平面上受到的垂直应力为

σ_z=γz+q （5.5-8）

对无黏性土，c=0，垂直墙背上的主动土压力强度为

p_a=（γz+q）K_a （5.5-9a）

其主动土压力强度分布图形为梯形，如图5.5-5所示。

图5.5-5 水平填土表面作用均布荷载

其方向如图5.5-5所示，作用点通过分布图形的形心。

总主动土压力为分布图形的面积

对于黏性土，垂直墙背上的主动土压力强度为

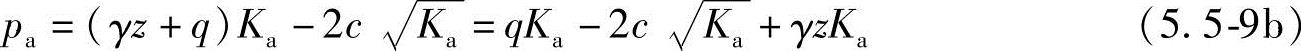
其主动土压力强度分布图形状视qK_a和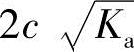的大小而定，可能呈现三角形或梯形分布，如图5.5-6所示。总主动土压力大小则为相应有效分布图的面积，作用位置通过有效分布图形心。

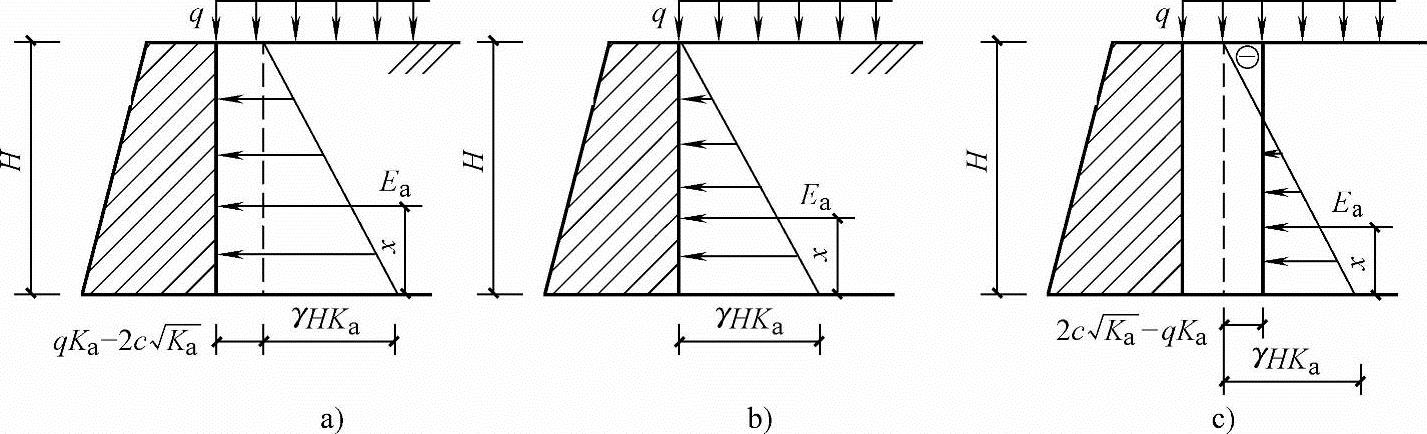
图5.5-6 黏性填土表面作用均布荷载时的主动土压力计算

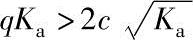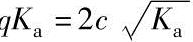a） b） c）

【例5.5-8】、【例5.5-9】 已知某挡土墙高5m，墙后填土水平，墙背垂直、光滑，填土重度γ=20kN/m³，内摩擦角φ=32°，填土面作用均布荷载q=20kPa。

【例5.5-8】 当墙后土体c=0时，用朗肯理论计算得到的主动土压力合力大小和距墙底的距离与下列哪组数值最接近？

（A）107.45kN/m，1.90m

（B）36.84kPa，1.90m

（C）6.14kPa，1.90m

（D）30.7kPa，1.90m

答案：（A）

图5.5-7 【例5.5-8】、【例5.5-9】图及结果

解答：主动土压力系数

在墙顶

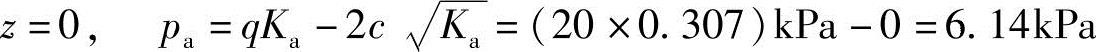
在墙底

主动土压力强度为梯形分布，如图5.5-7a所示。

总主动土压力合力大小：梯形图形的面积，。

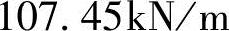作用点：，107.45x=76.75+127.92=204.67，距墙踵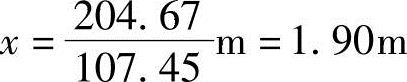，方向垂直指向墙背。

【例5.5-9】 当墙后土体c=10kPa时，用朗肯理论计算得到的墙顶主动土压力强度数值和主动土压力合力大小与下列哪组数值最接近？

（A）25.76kPa，54.1kN/m （B）36.84kPa，107.45kN/m

（C）-4.94kPa，54.1kN/m （D）6.14kPa，107.45kN/m

答案：（C）

解答：主动土压力系数

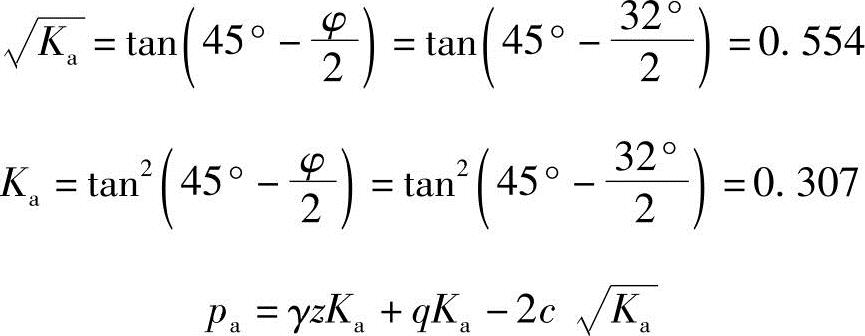
在墙顶

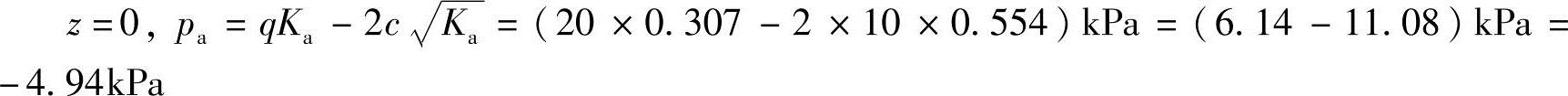
在墙底

z=H=10m

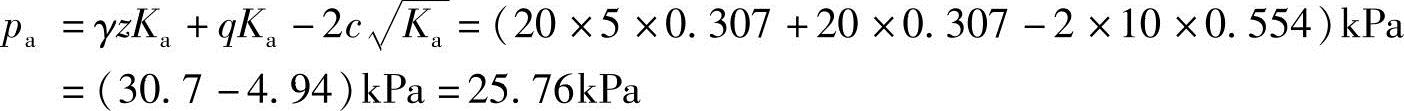
主动土压力强度为三角形分布，如图5.5-7b所示。

受拉区深度可由下述方法求得

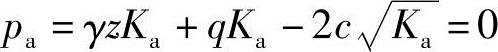
则

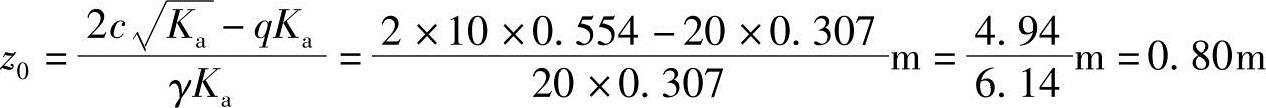
总主动土压力

负值部分忽略，三角形有效图形的面积。

作用点：距墙踵，方向垂直指向墙背。

（2）成层填土 当墙后填土成层，利用朗肯理论计算某深度z处的主动土压力时，先在该处取微元体，求出微元体水平面上的垂直应力σ_z，然后求出该处主动土压力强度

其中，K_ai由第i土层的内摩擦角φ_i求得，c_i为第i土层的黏聚力，在土层分界面处需分别计算上、下土层的主动土压力值。绘出分布图，再由分布图的面积求总主动土压力合力大小。

对无黏性土，主动土压力分布如图5.5-8a、b所示。

【例5.5-10】～【例5.5-14】 挡土墙高H=6m，墙背垂直光滑，填土为成层土，各层土的指标如图5.5-9所示。（主动土压力增大系数取1.0）

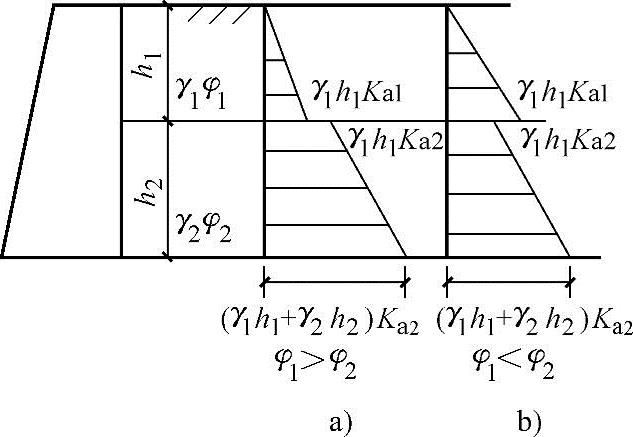
图5.5-8 成层填土主动土压力分布

图5.5-9 【例5.5-10】～【例5.5-14】图及结果

【例5.5-10】 试问第一层和第三层土的主动土压力系数与下列哪组数值最接近？

（A）K_a1=0.333，K_a3=0.455 （B）K_a1=0.577，K_a3=0.675

（C）K_a1=0.49，K_a3=0.455 （D）K_a1=0.333，K_a3=0.49

答案：（A）

解答：计算各分层主动土压力系数

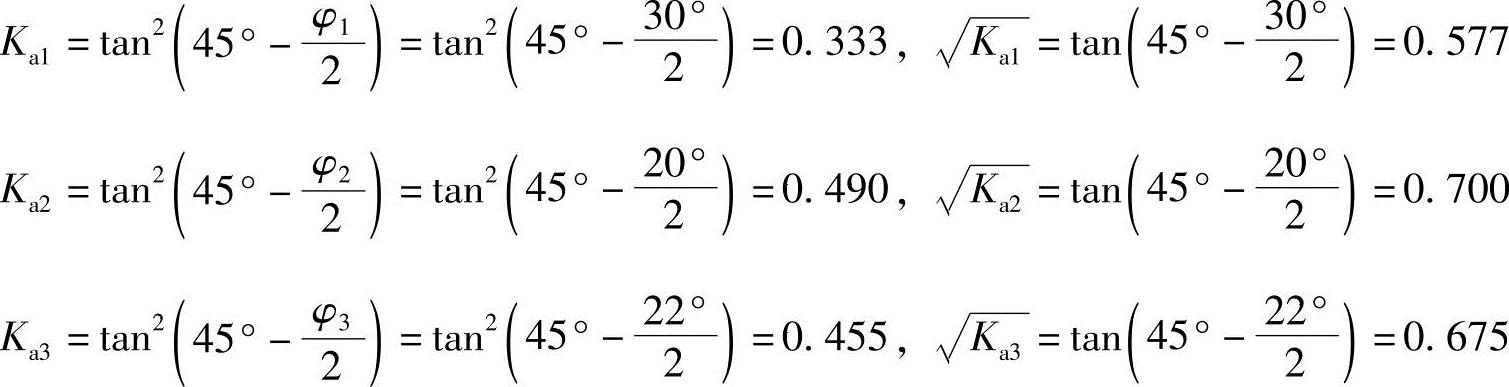
【例5.5-11】 试问第一层土底面处的主动土压力强度与下列哪项数值最接近？

（A）-5.92kPa （B）5.49kPa （C）5.92kPa （D）6.49kPa

答案：（B）

解答：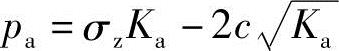

垂直压力

σ_z=∑γ_ih_i

A处：σ_zA=0，c=0，p_aA=0

C处：σ_zC=γ₁h₁=16.5×1kPa=16.5kPa，p_aC上=σ_zCK_a1-0=16.5×0.333kPa=5.49kPa

【例5.5-12】 试问第二层土顶面和底面处的主动土压力强度与下列哪组数值最接近？

（A）-5.92kPa，17.14kPa （B）5.49kPa，17.14kPa

（C）-5.92kPa，11.73kPa （D）5.49kPa，11.73kPa

答案：（C）

解答：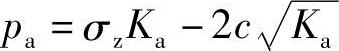

C处：

D处：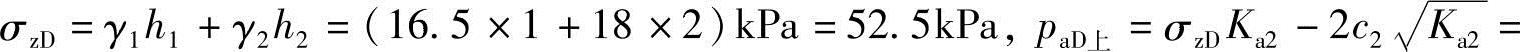

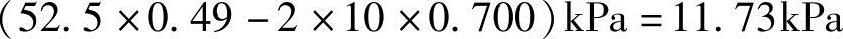
【例5.5-13】 试问第三层土顶面和底面处的主动土压力强度与下列哪组数值最接近？

（A）52.5kPa，112.5kPa （B）5.49kPa，44.44kPa

（C）11.73kPa，44.44kPa （D）17.14kPa，44.44kPa

答案：（D）

解答：D处：

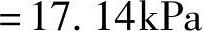
B处：

绘制主动土压力强度分布图，标出土压力强度数值，如图5.5-9所示。

【例5.5-14】 试问主动土压力合力E_a以及距墙底距离与下列哪组数值最接近？

（A）44.44kN/m，1.55m （B）44.44kN/m，1.33m

（C）102.92kN/m，1.55m （D）102.92kN/m，1.33m

答案：（C）

解答：计算总主动土压力E_a：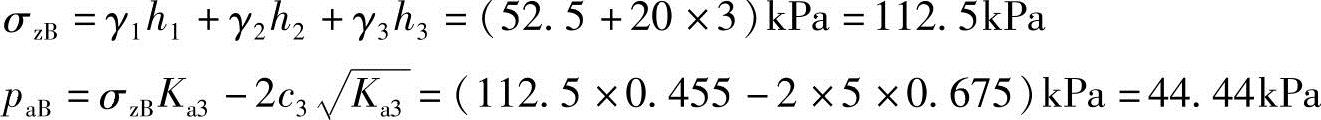

总主动土压力为土压力强度分布图面积，由三角形比例关系可求得第二层土中正应力强度分布范围为

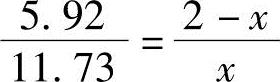
解得x=1.33m。

总主动土压力大小

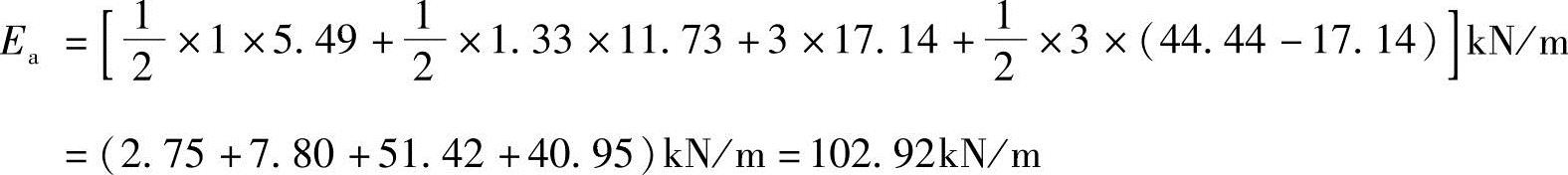
合力作用点

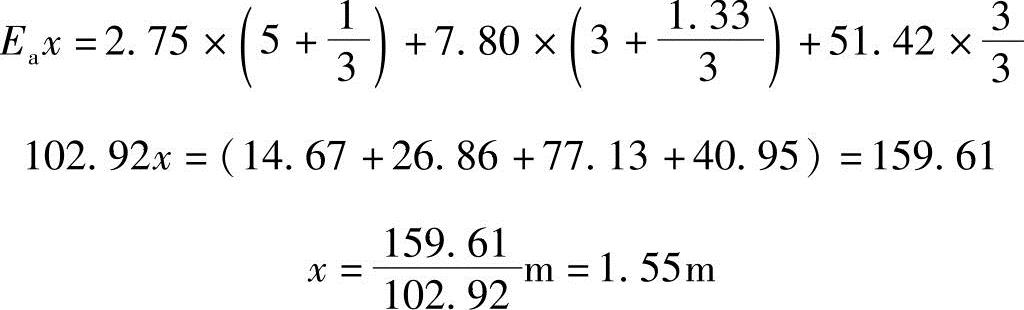
合力作用方向如图5.5-9所示。

（3）填土中存在地下水 当填土中有地下水时，水的存在不仅影响土的重度γ，水上、水下的φ常不同。计算土压力时可与成层土情况一样处理，只是当土层处于水下时采用浮重度γ′，φ取水下值进行土压力计算。而且除考虑土压力外，还应考虑作用于墙背的水压力，土压力与水压力的矢量和为作用于墙背上的侧压力。图5.5-10给出了水上、水下φ值相同时的土压力和水压力分布及合力方向，其作用点通过分布图的形心。

图5.5-10 地下水对土压力的影响

【例5.5-15】～【例5.5-18】 图5.5-11中挡土墙高5m，地下水位位于地表下3m处，土层参数如图5.5-11所示。（主动土压力增大系数取1.0）

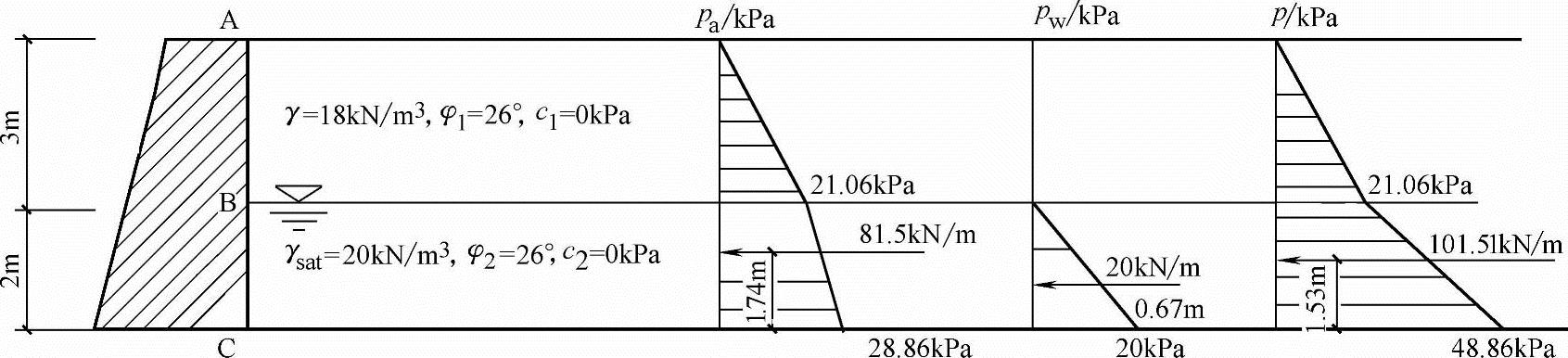
图5.5-11 【例5.5-15】～【例5.5-18】图及计算结果

【例5.5-15】 试问第一层土底面处的主动土压力强度与下列哪项数值最接近？

（A）21.06kPa （B）28.86kPa （C）54kPa （D）74kPa

答案：（A）

解答：主动土压力系数

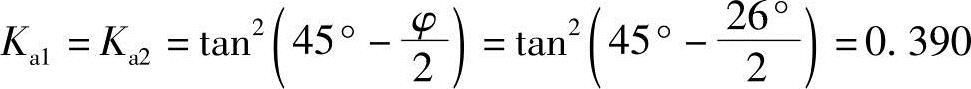
A：σ_zA=0，c=0，p_aA=0

B：σ_zB=（18×3）kPa=54kPa，p_aB=σ_zBK_a1=（54×0.390）kPa=21.06kPa

【例5.5-16】 试问第二层土底面处的主动土压力强度与下列哪项数值最接近？

（A）20.0kPa （B）21.06kPa （C）28.86kPa （D）48.86kPa

答案：（C）

解答：C点：σ_zC=（54+2×10）kPa=74kPa，p_aC=σ_zCK_a2=（74×0.390）kPa=28.86kPa

【例5.5-17】 试问挡土墙上的总主动土压力数值及距墙底的合力作用位置与下列哪组数值最接近？

（A）28.86kN/m，1.74m （B）48.86kN/m，1.53m

（C）81.51kN/m，1.74m （D）101.1kN/m，1.53m

答案：（C）

解答：主动土压力合力大小

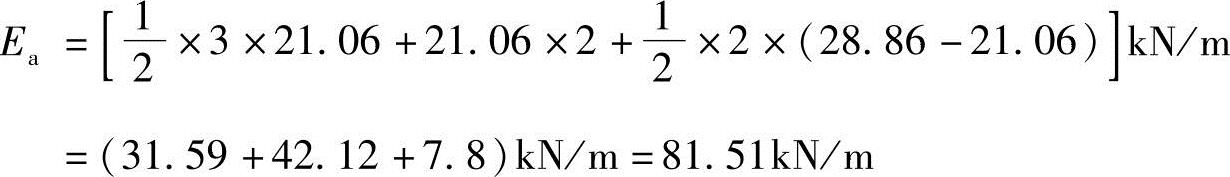
合力位置

【例5.5-18】 试问挡土墙上的总侧压力数值及距墙底的合力作用位置与下列哪组数值最接近？

（A）28.86kN/m，1.74m （B）48.86kN/m，1.53m

（C）81.51kN/m，1.74m （D）101.1kN/m，1.53m

答案：（D）

解答：水压力 总压力

A：p_wA=0 p_A=0

B：p_wB=0 p_B=21.06kPa

C：p_wC=（2×10）kPa=20kPa p_C=（28.86+20）kPa=48.86kPa

水压力合力

位置

（1/3×2）m=0.67m

总侧压力

E=E_a+E_w=（81.51+20）kN/m=101.51kN/m

位置

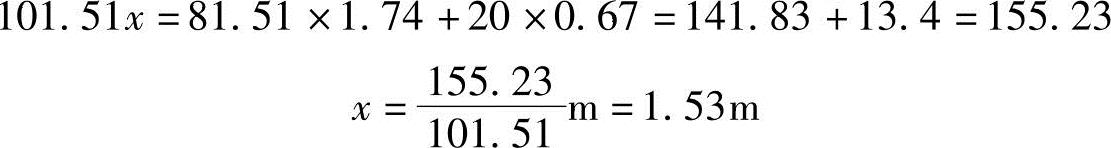
合力方向均垂直指向墙背，如图5.5-11所示。

【例5.5-19】～【例5.5-25】 挡土墙的墙背垂直、光滑，墙高5m，墙后填土表面水平，填土物理力学性质指标如图5.5-12所示。（主动土压力增大系数取1.0）

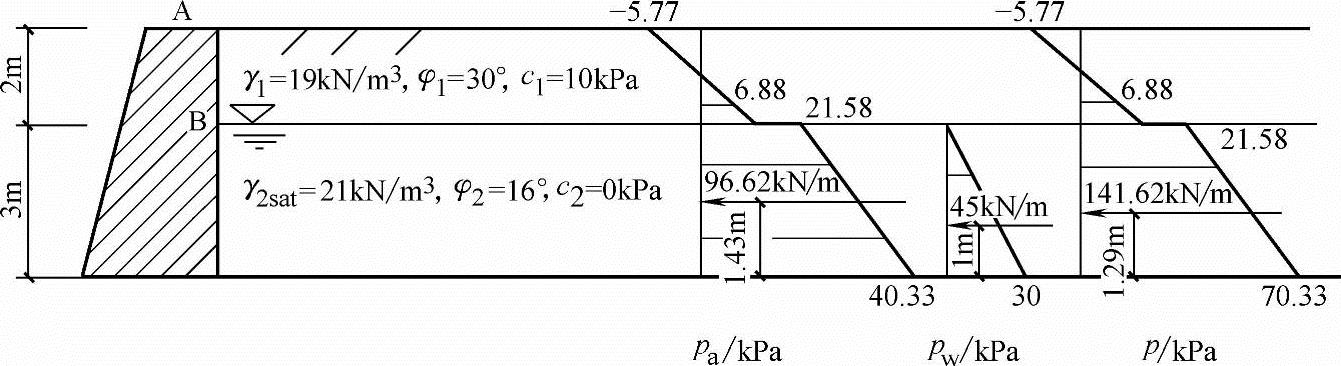
图5.5-12 【例5.5-19】～【例5.5-25】图及计算结果

【例5.5-19】 试问两层土的主动土压力系数与下列哪组数值最接近？

（A）K_a1=0.333，K_a2=0.754 （B）K_a1=0.577，K_a2=0.754

（C）K_a1=0.577，K_a2=0.568 （D）K_a1=0.333，K_a2=0.568

答案：（D）

解答：计算主动土压力系数

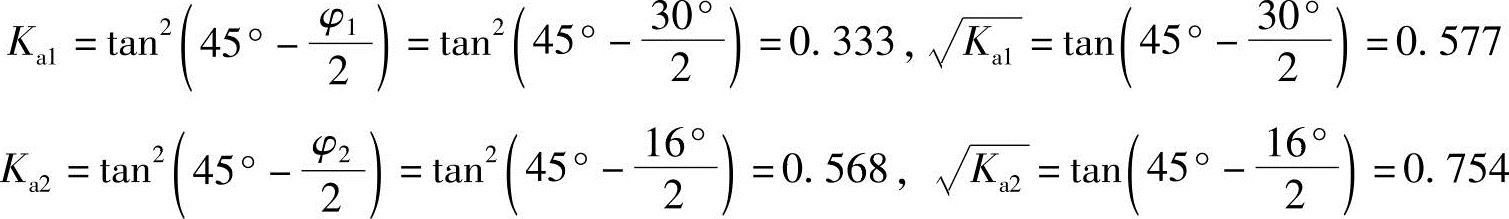
【例5.5-20】 试问第一层土顶面处的主动土压力强度与下列哪项数值最接近？

（A）0kPa （B）-3.33kPa （C）-5.77kPa （D）-7.54kPa

答案：（C）

解答：A：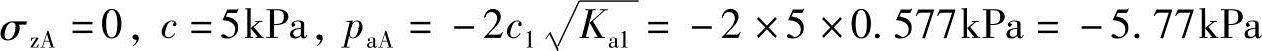

【例5.5-21】 试问第一层土底面处的主动土压力强度与下列哪项数值最接近？

（A）6.88kPa （B）7.88kPa （C）8.88kPa （D）9.88kPa

答案：（A）

解答：B：

【例5.5-22】 试问第二层土顶面和底面处的主动土压力强度与下列哪组数值最接近？

（A）38kPa，71kPa （B）21.58kPa，40.33kPa

（C）6.88kPa，40.33kPa （D）21.58kPa，71kPa

答案：（B）

解答：B：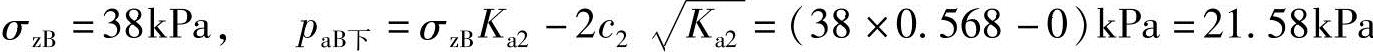

C：σ_zC=（38+3×11）kPa=71kPa， p_aC=σ_zCK_a2=（71×0.568）kPa=40.33kPa

【例5.5-23】 试问受拉区深度与下列哪项数值最接近？

（A）0.91m （B）1.09m （C）0.81m （D）1.19m

答案：（A）

解答：由三角形比例关系可求得第一层土中受拉区深度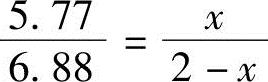，，解得x=0.91m。

【例5.5-24】 试问挡土墙上的总主动土压力大小及距墙底的合力作用位置与下列哪组数值最接近？

（A）6.88kPa，1.43m （B）21.58kPa，1.43m

（C）40.33kPa，1.43m （D）96.62kN/m，1.43m

答案：（D）

解答：由受拉区深度得正应力强度分布范围为

（2-0.91）m=1.09m

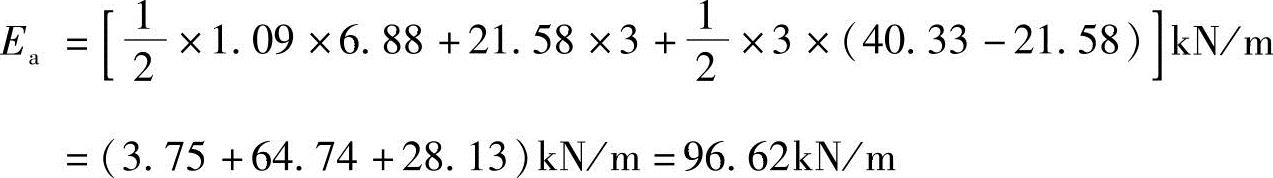
作用位置：

距墙底

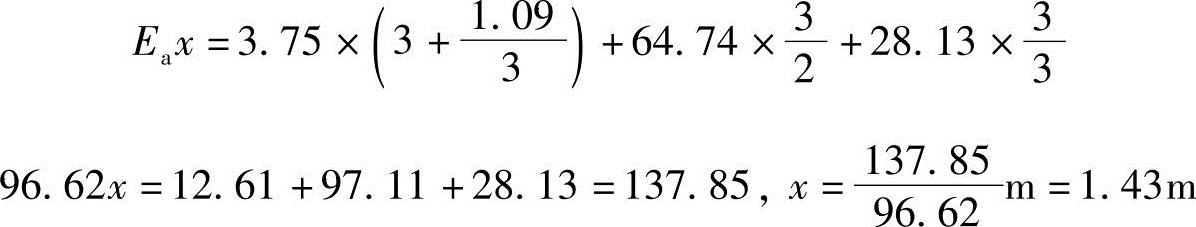
【例5.5-25】 试问挡土墙上的总侧压力及合力作用位置距墙底与下列哪组数值最接近？

（A）96.62kN/m，1.43m （B）141.62kN/m，1.43m

（C）96.62kN/m，1.29m （D）141.62kN/m，1.29m

答案：（D）

解答：水压力p_wB=0，B点总压力等于主动土压力。

水压力p_wC=（3×10）kPa=30kPa，总压力p_C=（40.33+30）kPa=70.33kPa。

总水压力合力

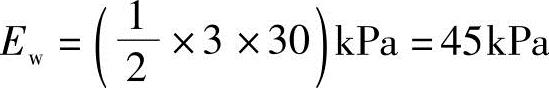
总的侧压力

E=E_a+E_w=（96.62+45）kPa=141.62kPa

总侧压力作用位置，距墙底