在一般情况下,变形毛坯内各质点的变形和受力状态是不相同的。通常将质点的受力状态称为点的应力状态。对同一点应力状态,6个应力分量的大小与所选坐标有关,不同坐标系所表现的6个应力分量的数值是不同的。对于板料冲压工艺,第二行应力状态居多。......
2023-06-26
地基附加应力是地基中增加的有效应力,对于地面作用大面积均布荷载和地下水位下降引起的地基附加应力计算方法简单,可以按照前述自重应力计算方法确定。对于有限尺寸的建筑物基础在地基中产生的附加应力,目前在求解时一般假定地基土是连续、均匀、各向同性的完全弹性体,根据弹性理论计算,并可利用叠加原理进行应力叠加、计算,矩形基础地基附加应力计算的角点法是常用方法;有时也采用简化方法,应力扩散角法就是其中之一。
1.地面作用大面积均布荷载
如图5.3-6所示,可以把大面积均布荷载p换算为一层和地基土体等重度的土,这层土的厚度h=p/γ,γ为地基土体的重度。加载前,地基中的自重应力σcz的分布图为由原地面算起的三角形;加载后,地基中自重应力σcz的分布图为由新地面算起的三角形,两条线平行,差值在各深度处都为γh=p。所以,由大面积均布荷载p所产生的附加应力图为上、下等值的矩形,其值为p。
2.地下水位下降
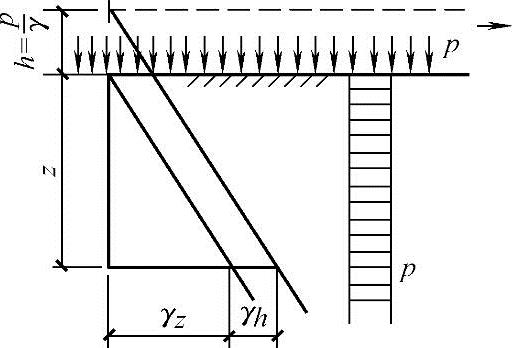
图5.3-6 地面大面积均布荷载
如图5.3-7所示,水位下降前,自重应力σcz分布为折线Oab,水位下降后为折线Oacd,其差值即为附加应力图形(图中阴影部分)。之所以产生附加应力,是由于水位下降高度h范围内,其计算重度由浮重度γ′变为天然重度γ,所以新水位以下附加应力值为(γ-γ′)h。
如果土层表面一直处在水面以下,比如处在低潮位以下的海底土层,海水潮位的变化不会产生附加应力,因为无论是高潮位还是低潮位,计算土层自重应力都是用浮重度。
【例5.3-17】、【例5.3-18】 某均匀粉质黏土土层,如图5.3-8所示,地下水位在地面下3m处,测得天然重度:水上为γ=17.5kN/m3,水下为γsat=18.0kN/m3。

图5.3-7 地下水位下降
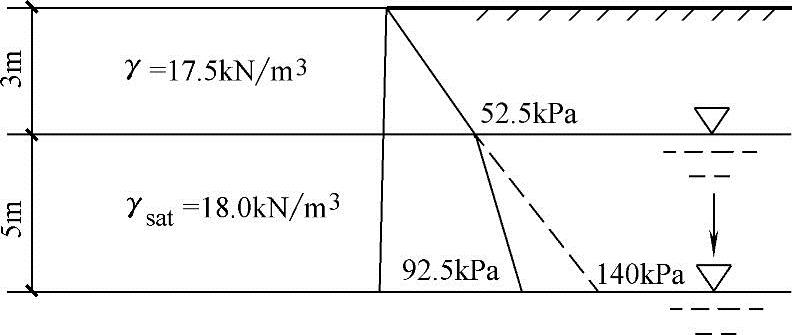
图5.3-8 【例5.3-17】、【例5.3-18】用图
【例5.3-17】 地面下8m处的竖向自重应力σcz数值与下列哪项最接近?
(A)52.5kPa (B)62.5kPa (C)92.5kPa (D)142.5kPa
答案:(C)
解答:

【例5.3-18】 如地下水位缓慢下降5m,水位下降后地面下8m处的竖向自重应力σcz数值与下列哪项数值接近。
(A)64kPa (B)92.5kPa (C)140.0kPa (D)144.0kPa
答案:(C)
解答:竖向自重应力为

从上面例题可见,由于地下水位下降导致土层的自重应力由92.5kPa增加到140kPa,这样对于下层土层来讲,就将会由于地下水位的下降产生47.5kPa的附加应力,因此下层可压缩土层将会产生附加变形。这就是很多城市由于大量抽吸地下水导致城市地面整体下沉的主要原因。
3.计算地基附加应力的角点法
在求解矩形基础下的地基附加应力时,因为一点的应力与三个方向坐标都有关系,需先求解矩形基础角点下的某深度处的附加应力,其他点下的附加应力需要采用叠加原理计算。根据荷载作用形式不同区别处理。
(1)矩形面积上竖向均布荷载作用下的竖向附加应力 当矩形基础底面受到竖直均布荷载作用时,基础的4个角点下任意深度z处的竖向附加应力均相同,可按下式计算
σzc=Kcp0 (5.3-8)
式中 p0——基底附加应力标准值或准永久组合值(kPa);
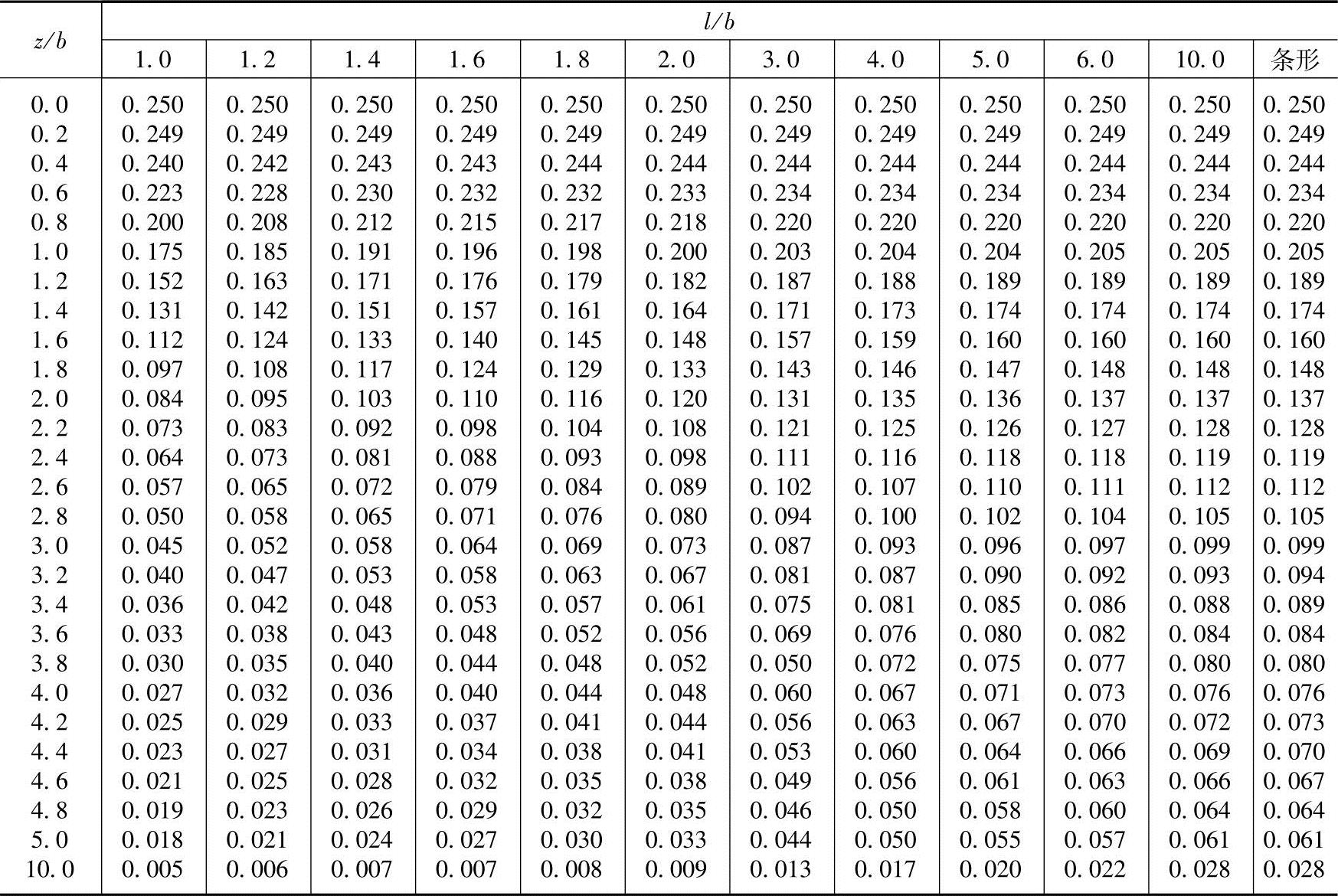
Kc——无因次附加应力系数,可根据l/b与z/b查表5.3-1。其中,l为矩形基础底面的长边(m);b为矩形基础底面的短边(m)。
表5.3-1 矩形面积上均布荷载作用下角点附加应力系数Kc值
对于在基底范围以内或以外任意点下的竖向附加应力,可利用式(5.3-8)并按叠加原理进行计算,这种方法称之为“角点法”。如图5.3-9a所示,设矩形基底abcd上作用着竖直均布荷载p,现要求在基底内M点以下任意深度z处的附加应力σzM。为此,通过M点分别做平行于基底长、短边的两根辅助线ef和gh,于是,M点就成为Ⅰ、Ⅱ、Ⅲ、Ⅳ4个新矩形基底的公共角点,则M点以下任意深度z处的附加应力为上述4个矩形基底对M点所产生的附加应力之和,即
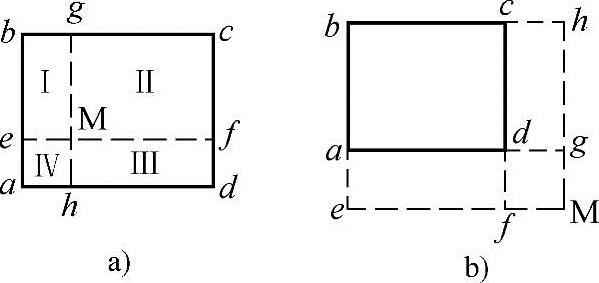
图5.3-9 计算点在基底范围内、外时的情况
σzM=σzI+σzII+σzIII+σzIV
若M点在基底范围之外,那么先将原有的基底扩大,使M点落在虚拟基底的角点上,如图5.3-9b中的虚线所示,再根据叠加原理求出M点以下任意深度z处的附加应力为
σzM=σzMhbe-σzMhcf-σzMgae+σzMgdf
应该指出,对于作用竖向均布荷载的矩形基底,在应用“角点法”时,需采用各个小矩形的长边l1和短边b1查表确定各小矩形角点的附加应力系数Kci,这里l1始终是小矩形基底的长边,b1为短边;而且角点必须是各个小矩形的公共角点。
【例5.3-19】~【例5.3-23】 如图5.3-10所示,矩形基础底面积L×B=6m×2m,基底上作用竖直均布荷载p0=300kPa。
【例5.3-19】 试问基底上A点以下深度z=2m处的竖向附加应力与下列哪项数值最接近?
(A)61kPa (B)82.2kPa
(C)115.8kPa (D)135.3kPa
答案:(C)
解答:为了求A点以下的附加应力,通过A点将基底划分为两块面积相等的矩形面积(2m×3m),这样A点就落在边长L1=3m、宽度B1=B=2m的两个矩形面积的公共角点上。根据L1/B1=3/2=1.5和z/B1=2/2=1,查表5.3-1得Kc=0.193,所以A点以下的附加应力为
σzA=2Kcp0=2×0.193×300kPa=115.8kPa
【例5.3-20】 试问基底上E点以下深度z=2m处的竖向附加应力与下列哪项数值最接近?
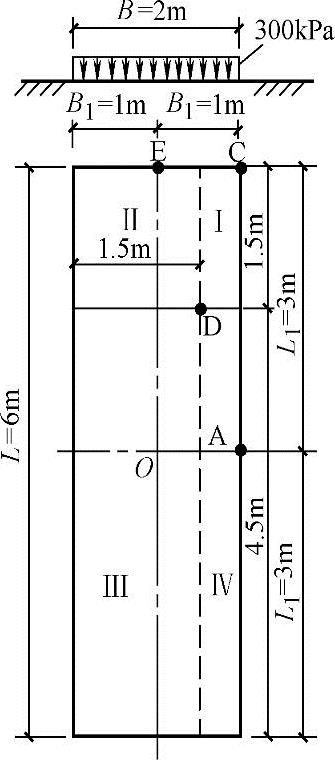
图5.3-10 【例5.3-19】~【例5.3-23】图
(A)61kPa (B)82.2kPa (C)115.8kPa (D)135.3kPa
答案:(B)
解答:为了求E点以下的附加应力,通过E点将基底划分为1m×6m的两块矩形面积,使E点落在边长L1=L=6m、宽度B1=1m的两个矩形面积的公共角点上。由L1/B1=6/1=6和z/B1=2/1=2,查表5.3-1得Kc=0.137,所以E点以下的附加应力为
σzE=2Kcp0=2×0.137×300kPa=82.2kPa
【例5.3-21】 试问基底上C点以下深度z=2m处的竖向附加应力与下列哪项数值最接近?
(A)61kPa (B)82.2kPa (C)115.8kPa (D)135.3kPa
答案:(A)
解答:C点正好落在边长L=6m、宽度B=2m的矩形面积的角点上,由L/B=6/2=3、z/B=2/2=1,查表5.3-1得Kc=0.203,则C点以下的附加应力为
σzC=Kcp0=0.203×300kPa=61kPa
【例5.3-22】 试问基底上D点以下深度z=2m处的竖向附加应力与下列哪项数值最接近?
(A)61kPa (B)82.2kPa (C)115.8kPa (D)135.3kPa
答案:(D)
解答:为了求D点以下的附加应力,通过D点分别做平行于基底长、短边的两根辅助线,将基底分割为Ⅰ、Ⅱ、Ⅲ、Ⅳ4块矩形面积,使D点落在这4块矩形面积的公共角点上,利用表5.3-1查得各块面积对D点的附加应力系数列于表5.3-2。
表5.3-2 【例5.3-22】中的竖向附加应力系数Kc计算表

于是,D点以下的附加应力为
σzD=∑Kcp=(0.06+0.138+0.177+0.076)×300kPa=135.3kPa
【例5.3-23】 试问基底上O点以下深度z=2m处的竖向附加应力与下列哪项数值最接近?
(A)82.2kPa (B)115.0kPa (C)135.3kPa (D)157.2kPa
答案:(D)
解答:为了求中心点O点以下的附加应力,同样可通过O点做平行于基底长、短边的两根辅助线,将基底分成4块相等的矩形面积,对于每一块面积来说,由L1/B1=3/1=3和z/B1=2/1=2,查表5.3-1得Kc=0.131,所以O点以下的附加应力为
σzO=4Kcp0=(4×0.131×300)kPa
=157.2kPa
由上述例题可见,对于作用均布荷载的矩形基础,在地基同样深度处,基底中心点下的地基附加应力最大;地基附加应力围绕着荷载中心位置向外扩散。
【例5.3-24】、【例5.3-25】 有甲、乙两个相距甚远的方形基础如图5.3-11所示,分别放在土层情况相同的地面上,其中甲基础的面积为4m×4m,乙基础的面积为1m×1m,基底均作用300kPa的竖直均布压力准永久组合值。
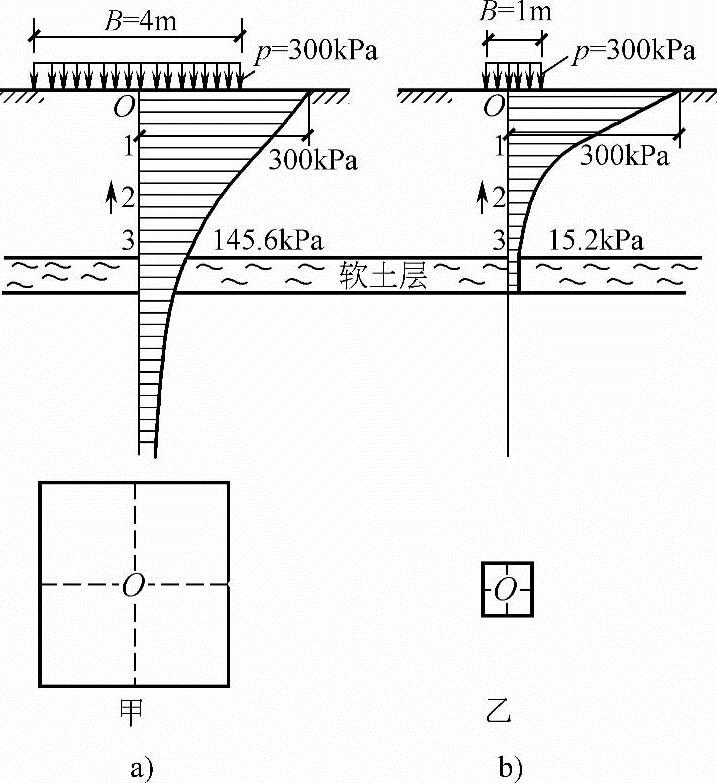
图5.3-11 【例5.3-24】、【例5.3-25】用图
【例5.3-24】 试问甲基础基底中心点O以下深度为1m、2m、3m处的竖向地基附加应力与下列哪项数值最接近?
(A)100.8kPa、32.4kPa、15.2kPa
(B)15.2kPa、32.4kPa、100.8kPa
(C)277.8kPa、210.2kPa、145.6kPa
(D)145.6kPa、210.2kPa、277.8kPa
答案:(C)
解答:通过甲基础基底中心点O分别做平行于基底两边的辅助线(如图5.3-11a中的虚线所示),于是将甲基础的底面划分为4个2m×2m的方形面积。因为中心点O均落在4个方形面积的公共角点上,利用“角点法”求得O点以下各深度上的竖向附加应力见表5.3-3,分布图如图5.3-11a所示。
【例5.3-25】 试问乙基础基底中心点O以下深度为1m、2m、3m处的竖向附加应力与下列哪项数值最接近?
(A)100.8kPa、32.4kPa、15.2kPa (B)15.2kPa、32.4kPa、100.8kPa
(C)277.8kPa、210.2kPa、145.6kPa (D)145.6kPa、210.2kPa、277.8kPa
答案:(A)
解答:同【例5.3-24】,将乙基础底面划分为4个0.5m×0.5m的方形面积,中心点O均落在4个方形面积的公共角点上,利用“角点法”求得O点以下各深度上的竖向地基附加应力见表5.3-4,分布图如图5.3-11b所示。
表5.3-3 【例5.3-24】中的甲基础中心点下竖向附加应力计算表
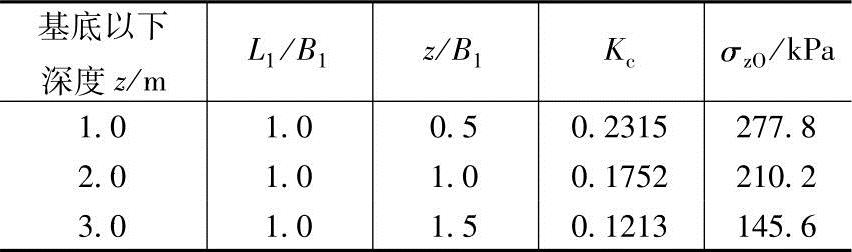
表5.3-4 【例5.3-25】中的乙基础中心点下竖向附加应力计算表
可见,地基中附加应力的分布与自重应力分布正好相反,以荷载作用范围为中心向外扩散,基底处最大,向侧向、向深处逐渐减小,但与深度呈非线性关系。
从计算结果可以看出,在强度相同的基底均布荷载作用下,基础底面积越大,附加应力传递得越深,或者说在同一深度处产生的附加应力越大。如图5.3-11所示,若离地面3m处有一高压缩性的软土层,对于甲基础,在软土层顶面产生145.6kPa的附加应力;而对于乙基础来说,在软土层顶面仅产生15.2kPa的附加应力。显然,前者的软土层将产生更大的变形,并导致基础产生较大的沉降。
【例5.3-26】 均布荷载准永久组合值p=250kPa作用于图5.3-12基底的阴影面积部分,试问A点以下3m处的地基附加应力与下列哪项数值最接近?
(A)200.95kPa (B)157.8kPa
(C)143.1kPa (D)107.8kPa
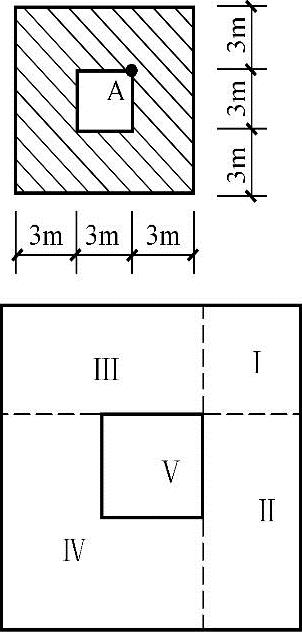
图5.3-12 【例5.3-26】图
答案:(B)
解答:如图5.3-12所示,将基底分成过A点的五块小矩形。
Ⅰ块: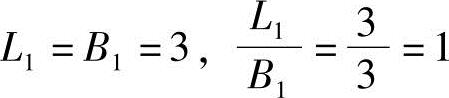 ,
,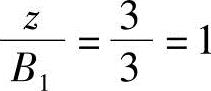 ,查表5.3-1得Kc1=0.1725。
,查表5.3-1得Kc1=0.1725。
Ⅱ块:L1=6,B1=3,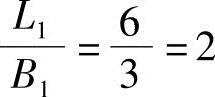 ,
,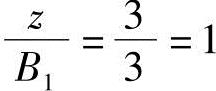 ,查表5.3-1得Kc2=0.1999。
,查表5.3-1得Kc2=0.1999。
Ⅲ块大小同Ⅱ,Ⅴ块大小同Ⅰ块。
Ⅳ块:L1=B1=6,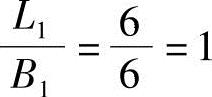 ,
,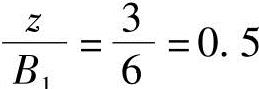 。
。
查表5.3-1内插得Kc4=0.1999,则
σzA=(Kc1+Kc2+Kc3+Kc4-Kc5)p
=[(0.1725+0.1999+0.1999+0.2315-0.1725)×250]kPa=157.8kPa
【例5.3-27】、【例5.3-28】 如图5.3-13所示,均布条形荷载p=150kPa,基础宽b=4m。
【例5.3-27】 试问B点下8m处的地基附加应力与下列哪项数值最接近?
(A)20.6kPa (B)41.1kPa
(C)22.8kPa (D)45.6kPa
答案:(B)
解答:条形基础也可以利用表5.3-1确定地基附加应力。
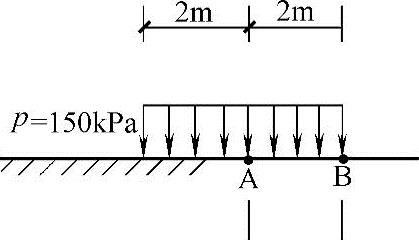
图5.3-13 【例5.3-27】、【例5.3-28】用图
由于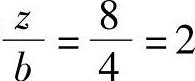 ,查5.3-1得Kc=0.137,与矩形基础相比,条形基础可看作无限长度,所以按照矩形基础确定角点处附加应力后需再乘2,获得条形基础边缘附加应力
,查5.3-1得Kc=0.137,与矩形基础相比,条形基础可看作无限长度,所以按照矩形基础确定角点处附加应力后需再乘2,获得条形基础边缘附加应力
σzB=2Kcp=(2×0.137×150)kPa=41.1kPa
【例5.3-28】 试问A点下8m处的地基附加应力与下列哪项数值最接近?
(A)20.6kPa (B)41.1kPa (C)22.8kPa (D)45.6kPa
答案:(D)
解答:条形基础中心也可以利用表5.3-1确定附加应力。
由于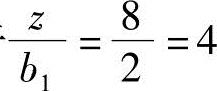 ,查表5.3-1得Kc=0.076,利用叠加原理,则
,查表5.3-1得Kc=0.076,利用叠加原理,则
σzA=4Kcp=(4×0.076×150)kPa=45.6kPa
(2)矩形面积上竖向三角形分布荷载作用下的竖向附加应力 矩形基底面积受竖向三角形分布荷载作用时,零荷载和最大荷载两个角点下的竖向附加应力按下式计算
σzT=KTpT (5.3-9)
式中 pT——基底附加压力标准值或准永久组合值最大值(kPa);
KT——无因次应力系数,可根据l/b与z/b查表得出(见《规范》附录表K.0.2)。其中,b为沿荷载变化方向矩形基底的边长(m);l为矩形基底的另一个边长(m)。
(3)圆形面积上竖向均布荷载作用下中点的竖向附加应力 当圆形基底面积受竖向均布荷载作用中点下任意深度z处的竖向附加应力按下式计算:
σzy=Kyp0 (5.3-10)
式中 p0——基底竖向附加压力标准值或准永久组合值分布值(kPa);
Ky——无因次应力系数,可根据z/r查表得出(见《规范》附录表K.0.3);其中,r为圆形基础的半径(m)。
4.应力扩散角法计算地基附加应力的简化方法
对于地基中存在软弱下卧层的情况,由于软层与持力层土的物理力学性质相差比较悬殊,采用前述线弹性理论计算地基附加应力会产生较大误差,为了简化计算,《规范》推荐采用应力扩散角法计算软弱下卧层顶部的地基附加应力。
假定作用的总竖向荷载不变,作用面积越大,分布荷载的数值越小,从基础底面开始,地基附加应力按照一定的扩散角向下扩散,《规范》给出了按照扩散角法计算距离基底深度为z位置处的地基附加应力的公式。
条形基础

矩形基础
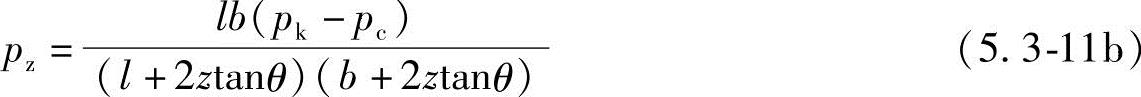
式中 pk——相应于作用的标准组合时,软弱下卧层顶面处的附加应力平均值(kPa);
b——矩形基础或条形基础底边的宽度(m);
l——矩形基础底边的长度(m);
pc——基础底面处土的竖向自重应力值(kPa);
z——基础底面至软弱下卧层顶面的距离(m);
θ——地面压力扩散线与垂直线的夹角(°),即地基压力扩散角,可按表5.3-5采用。
【例5.3-29】、【例5.3-30】 图5.3-14所示地基持力层和基础埋深范围为黏性土,厚度4.0m,水上重度为18.2kN/m3,水下重度为18.5kN/m3,压缩模量为7.5MPa;持力层下为淤泥质土,压缩模量为2.5MPa。(计算基础和土自重时取γG=20kN/m3)
表5.3-5 地基压力扩散角θ
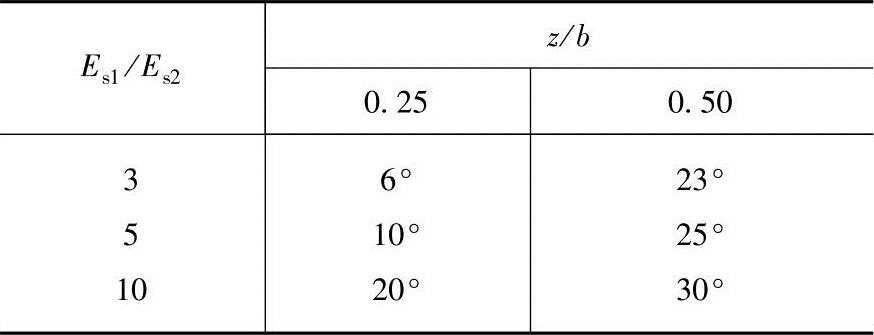
注:1.Es1为上层土压缩模量,Es2为下层土压缩模量。
2.z/b<0.25时,取θ=0°,必要时,宜由试验确定;z/b>0.50时,θ值不变。
3.z/b在0.25与0.5之间可插值使用。
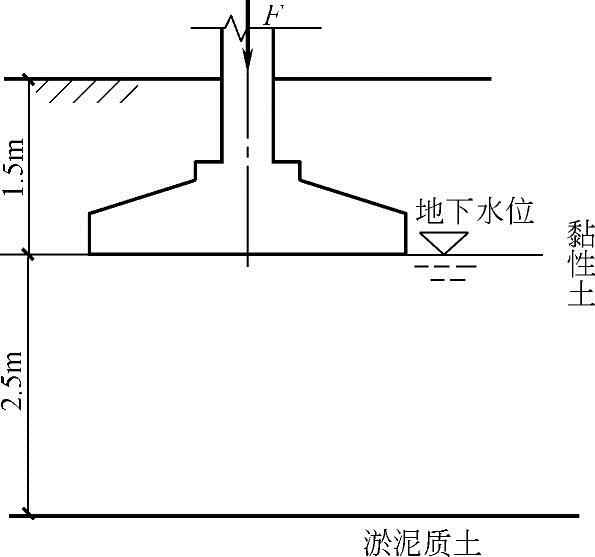
图5.3-14 【例5.3-29】和【例5.3-30】用图
【例5.3-29】 若基础为柱下独立基础,作用于基础顶部的中心竖向荷载标准值为Fk=1100kN,基础底面尺寸l×b=3.0m×2.2m,试问软弱下卧层顶部的附加应力标准值与下列哪项数值最接近?
(A)50.5kPa (B)54.6kPa (C)169.4kPa (D)196.7kPa
答案:(A)
解答:基础和填土自重
Gk=γGkdA=20dA=20×1.5×3.0×2.2kN=198kN
基底平均压力标准值为
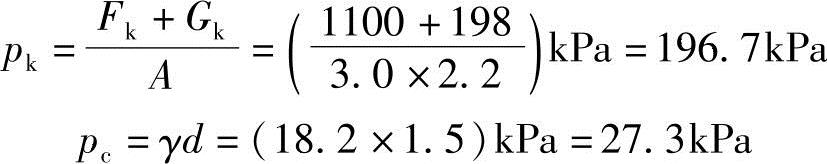
由于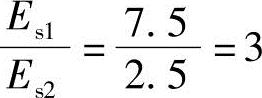 ,z=2.5m,z/b=2.5/2.2=1.14>0.5,查表5.3-5得θ=23°
,z=2.5m,z/b=2.5/2.2=1.14>0.5,查表5.3-5得θ=23°
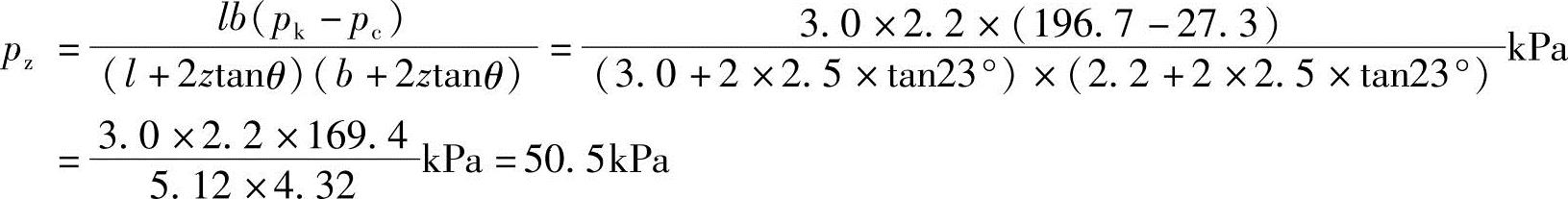
【例5.3-30】 若基础为墙下条形基础,作用于基础顶部的中心竖向荷载标准值为800kN/m,基础底面宽度b=3.0m,试问软弱下卧层顶部的附加应力标准值与下列哪项数值最接近?
(A)149.1kPa (B)157.0kPa (C)157.9kPa (D)165.8kPa
答案:(C)
解答:基础和填土自重
Gk=γGdb=20db=20×1.5×3.0kN/m=90kN/m
基底平均压力为

由于 ,z/b=2.5/3.0=0.83>0.5,查表5.3-5得θ=23°
,z/b=2.5/3.0=0.83>0.5,查表5.3-5得θ=23°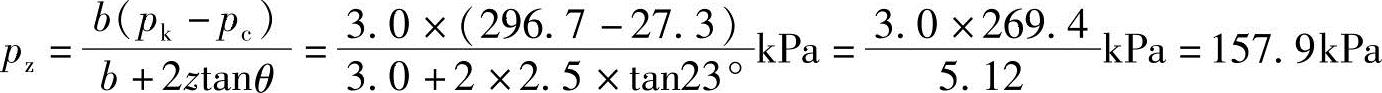
有关全国一、二级注册结构工程师专业考试教程的文章

在一般情况下,变形毛坯内各质点的变形和受力状态是不相同的。通常将质点的受力状态称为点的应力状态。对同一点应力状态,6个应力分量的大小与所选坐标有关,不同坐标系所表现的6个应力分量的数值是不同的。对于板料冲压工艺,第二行应力状态居多。......
2023-06-26

铝条带长度与物质损耗的关系,可以用背应力的作用来进行解释。图8.6钛化氮基线上的一条铝质短条带的示意在分析这样的应力状态影响时,人们提出了在电场力和机械力的综合作用下的原子扩散过程为不可逆转的物理过程的设想。我们应注意到,上文中的背应力是由电迁移引起的,但外加应力和电迁移之间的相互作用是相同的。例如,在阳极施加的压应力会延缓电迁移现象。......
2023-06-20

额外附加成交及其他在下面的这个例子中,金克拉想说的意思是推销之外的一些事情及其对成交的效应。金克拉认为强尼是全美最佳的擦鞋童,但他仍然认为,只要金克拉给予他一点附加的鼓励,他还是可以做得更好。金克拉告诉他,他的工作成效极佳,他让金克拉的鞋子看来洁净无比。更重要的是,强尼并不会满足于一次一项的交易,只要他发现机会,他就会加以充分利用,以做成第二笔交易。......
2024-07-23

传统的方法都是通过附加质量法来计算结构在水中的模态,即湿模态,本文利用APDL语言命令流和Workbench平台耦合的方法来实现对转子部件在预应力情况下湿模态的计算。插入命令流如下求解之后,前三阶振型图如图5.4-4所示图5.4-4 湿模态前三阶振型图则前六阶固有频率如图5.4-5所示。另外由图5.4-4可以看出,在水中各阶振型对应的振幅相比于在真空中也相应降低,这是水介质阻尼作用的结果。......
2023-06-26

可灌性是指砂砾石地基能接受灌浆材料灌入程度的一种特性。不均匀系数Cu式中D60——砂砾石颗粒级配曲线上相应于含量为60%的粒径,mm;D10——砂砾石颗粒级配曲线上相应于含量为10%的粒径,mm。Cu的大小反映了砂砾石颗粒不均匀的程度。当Cu较小时,砂砾石的密度较小,透水性较大,可灌性较好;当Cu较大时,透水性小,可灌性差。......
2023-06-29

随着制备用的反渗透膜结构的不同,有弱酸性超纯水也有中性超纯水。煮沸后,钙、镁易与碳酸根生成水垢而析出。矿泉水中的溴酸盐近年来,矿泉水企业普遍采用臭氧杀菌工艺。正常情况下,水中不含溴酸盐,但普遍含有溴化物。国际癌症研究中心认为溴酸钾对实验动物有致癌作用,但溴酸盐对人的致癌作用还不能肯定,为此将其列为对人体可能致癌的物质。2004年世界卫生组织在《饮用水水质准则》中,将水中溴酸盐的限量值定为0.01mg/L。......
2023-07-04

任何焊接结构件中都不可避免焊接应力的存在,并且直接影响焊接结构的制造质量和安全使用性能。当[σmax]接近于屈服强度时,焊接残余应力的影响逐渐消失。(二)对刚度的影响焊接残余应力与外载引起的应力相叠加,可能使工件局部提前屈服产生塑性变形,工件的刚度会因此而降低。残余应力对稳定性的影响取决于杆件的几何形状和内应力分布。所以焊接残余应力的存在对工件的加工精度有不同程度的影响。......
2023-06-23

11.6.3 压差阻力物体在流体中运动时因为物体前后压力差引起的阻力称为压差阻力,其形成原因与物体的形状有关,所以压差阻力又称为形状阻力,这里针对其形成原因、影响因素和改善措施描述如下。......
2023-06-29
相关推荐