心理学家艾丽娅·克拉姆和她的同事开发了压力思维模式测试,以评估人们对压力的看法。思维模式2:压力有促进作用。根据美国心理学协会的调查,多数人认为他们承受的压力水平不健康。克拉姆的研究表明,相信压力有促进作用的人,比那些认为压力有害的人,更少抑郁,对生活更满意。然而,克拉姆的研究表明,这些性格特点都无法解释压力思维模式对健康、幸福或者工作效率的影响。......
2024-01-19
1.基底压力
建筑物荷载通过基础向地基土层中传递,首先在基础与地基的接触面产生应力,即基底压力,然后在地基土层中产生附加应力,引起基础沉降。
外部荷载与上部建筑和基础的全部重量,都是通过基础底面传递到地基,在基础与地基的接触面上的有效接触应力称为基底压力。其分布比较复杂,与基础与地基的相对刚度、基础埋深、荷载大小及分布、地基土的性质都有关系。对于刚性基础在工程实用中常采用下列简化算法,按线性分布处理。
(1)轴心荷载 当上部竖向荷载的合力通过基础底面的形心时,基底压力均匀分布,按下式计算

式中 pk——相应于荷载效应标准组合时,基础底面处的平均压力值(kPa);
Fk——相应于荷载效应标准组合时,上部结构传至基础顶面的竖向力值(kN);
Gk——基础自重和基础上的土重(kN);
A——基础底面面积(m2)。
对于条形基础,当基础底面为b时

式中 Fk——相应于荷载效应标准组合时,上部结构传至基础顶面的竖向线荷载值(kN/m);
Gk——单位长度基础自重和基础上的土重(kN/m)。
(2)偏心荷载 常见的偏心荷载往往作用于矩形基础的一个主轴上,此时基础底面边缘的压力按下式计算

式中 pkmax、pkmin——相应于荷载效应标准组合时,基础底面边缘的最大、最小基底压力(kPa);
e——竖向合力的总偏心距(m);
l——力矩作用方向的基础底面边长(m)。
对于条形基础在长度方向上取1m计算,式(5.3-4)中的Fk+Gk代入每延米数值,A以基宽b代入。
由式(5.3-4)可知,l为产生偏心方向的矩形基础边长,(Fk+Gk)合力作用位置不同,基底压力可有如图5.3-3所示的几种分布图形
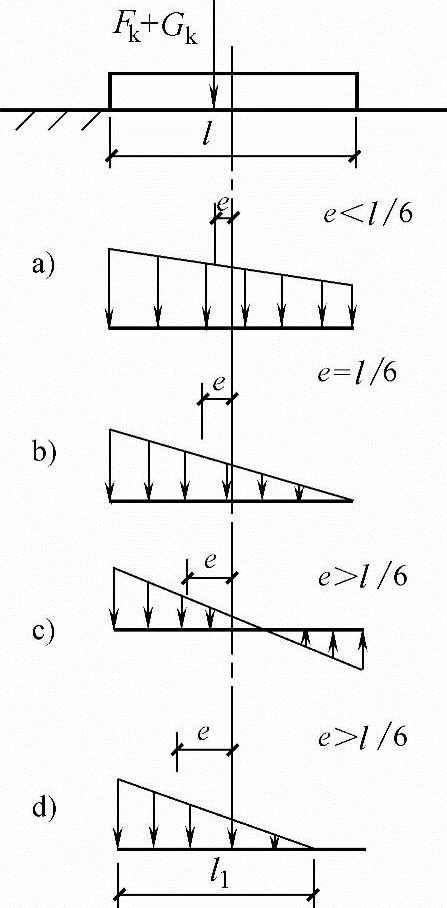
图5.3-3 基底压力分布图
1)当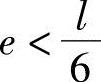 时,基底压力呈梯形分布。
时,基底压力呈梯形分布。
2)当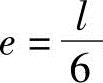 时,基底压力呈三角形分布。
时,基底压力呈三角形分布。
3)当 时,基底出现拉应力,而土体属弱拉材料,不能承受拉力,将导致基底压力的重分布,假定呈三角形分布的分布范围宽度为
时,基底出现拉应力,而土体属弱拉材料,不能承受拉力,将导致基底压力的重分布,假定呈三角形分布的分布范围宽度为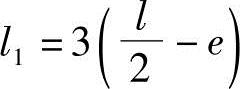 ,则基底压力为
,则基底压力为

建筑物或基础处于水下还需要考虑浮力作用,在计算外力Fk时,自重部分需考虑水下浮力作用。计算基础和填土自重Gk时,采用下列公式
Gk=γGdA (5.3-6a)
式中 γG——基础和填土的平均重度(kN/m3),一般处于水上取20kN/m3,完全处于水下取10kN/m3;
A——基础底面面积(m2),矩形基础为A=lb,条形基础为A=1×b;
d——基础埋置深度(m),当室内外地面高差较大时,取平均值。
当基础有一部分处于水下时,基础及填土自重Gk按下式计算:
Gk=γGdA-γwdwA=20dA-10dwA (5.3-6b)
式中 dw——基础底面至地下水位面的距离。
2.基底附加压力
当基础建于地面以下,基础埋置深度为d,在基础底面处原来已作用自重应力,基底处在原有应力基础上增加的有效应力称为基底附加压力,以p0表示,应在基底压力中扣除自重应力计算,即
p0=pk-σcd=pk-γd (5.3-7)
式中 p0——基底附加压力(kPa);
pk——基底压力(kPa);
σcd——基底处的地基竖向自重应力(kPa);
γ——基础埋深范围内地基土的加权平均重度(kN/m3),水下取浮重度。
基底附加压力将在地基中产生地基附加应力,是产生基础沉降的主要原因。
由式(5.3-7)可见,对于箱形或筏形基础,如果基底压力不变,基础埋置深度越大,则基底附加压力越小。若使得
p0=pk-γd=0
此时基底压力等于基底处的自重应力,基底附加压力为零,基础几乎没有沉降,这样的基础称为补偿式基础或浮式基础。建筑物的重量正好“补偿”了挖取的土重,基础几乎不下沉,“浮”在基底。基底附加压力适当减少的基础称为部分补偿基础。
因此,当地基承载力不太高的时候,为了减少建筑物基础沉降,可以采取的措施之一是减少基底附加压力。为了减少基底附加应力,一方面可以通过增大基坑开挖深度,增加基础埋置深度;另一方面可以通过在开挖位置上修建空腔建筑来降低基础和回填土的自重。例如高层建筑基础往往建在天然地面以下8~10m,甚至更深,不仅如此,在地下部分往往修建2~3层的地下室。
【例5.3-4】~【例5.3-7】 柱下独立基础长为4m,宽为2m,埋深1.5m,作用于地面的上部竖向外荷载标准值为640kN,地下水位以上基础和填土自重可按γG=20kN/m计算。
【例5.3-4】 试问地下水埋藏很深时的基底压力与下列哪项数值最接近?
(A)95kPa (B)110kPa (C)190kPa (D)335kPa
答案:(B)
解答:
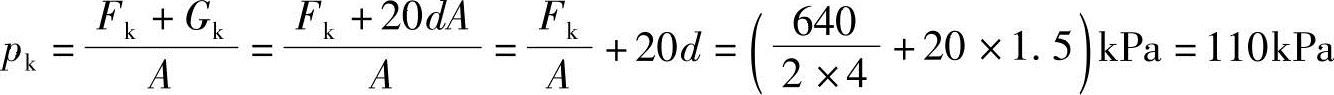
【例5.3-5】 试问地下水位位于基底时的基底压力与下列哪项数值最接近?
(A)95kPa (B)110kPa (C)190kPa (D)335kPa
答案:(B)
解答:
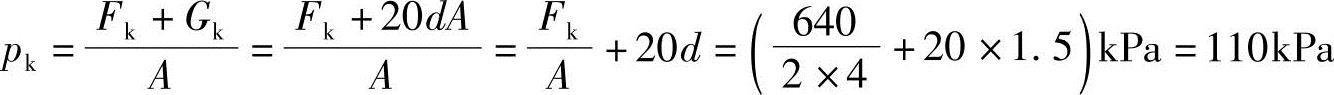
【例5.3-6】 试问地下水位位于基底以上1m时的基底压力与下列哪项数值最接近?
(A)95kPa (B)100kPa (C)105kPa (D)110kPa
答案:(B)
解答:
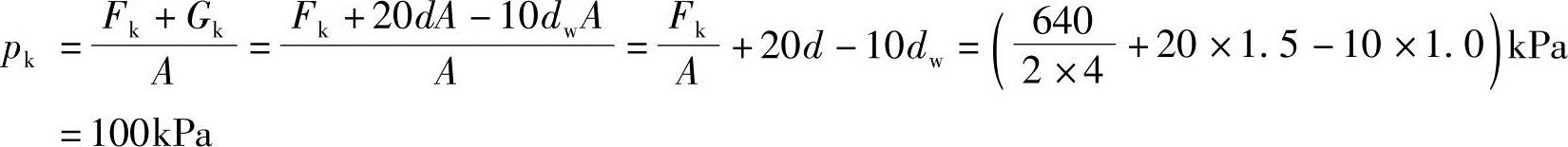
【例5.3-7】 试问地下水位位于地面处的基底压力标准值与下列哪项数值最接近?
(A)95kPa (B)110kPa (C)105kPa (D)110kPa
答案:(A)
解答:
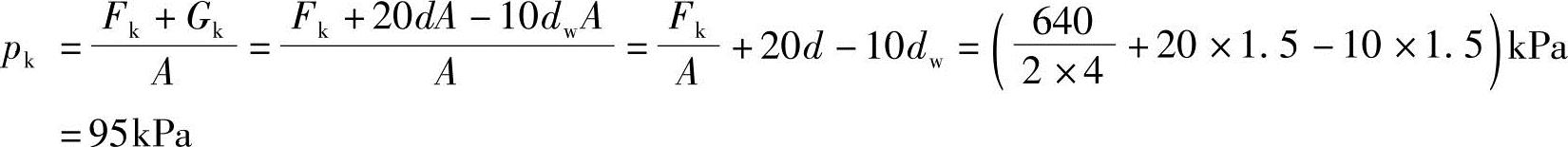
【例5.3-8】 墙下条形基础宽为3m,埋深1.2m,地下水埋藏很深,上部竖向外荷标准值为810kN,试问基底压力标准值与下列哪项数值最接近?
(A)270kPa (B)282kPa (C)294kPa (D)330kPa
答案:(C)解答: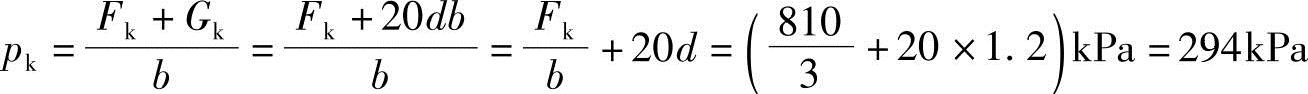
【例5.3-9】 墙下条形基础宽为3m,埋深1.2m,地下水埋藏很深,基础底面处总竖向力标准值为810kN,偏心距为0.2m,试问基底压力标准值平均值和最大值与下列哪项数值最接近?
(A)270kPa,270kPa (B)282kPa,394.8kPa
(C)294kPa,411.6kPa (D)270kPa,378kPa
答案:(D)
解答:平均值: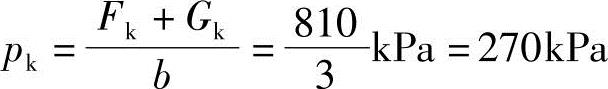
对基础中心的合力偏心距为0.2m,因为e=0.2m<(3/6)m=0.5m,所以基底压力分布为梯形。
最大基底压力直接用式(5.3-4)计算
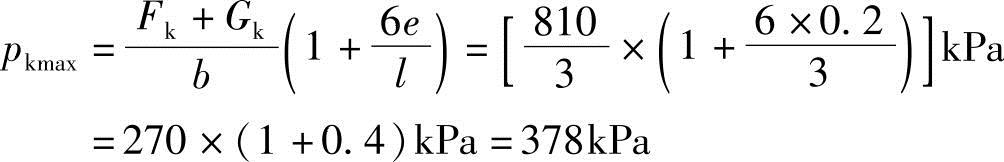
【例5.3-10】~【例5.3-13】 地基分布如图5.3-4所示,地下水位在地面下1.1m处,柱下独立基础长为4m、宽为3m,作用在地面处的竖向力标准值为900kN,弯矩标准值为210kN·m。
【例5.3-10】 试问基底压力标准值最大值与下列哪项数值最接近?
(A)101.3kPa
(B)132.3kPa
(C)141.0kPa
(D)141.3kPa
答案:(B)
解答:作用在基础底面中心的总竖向力为
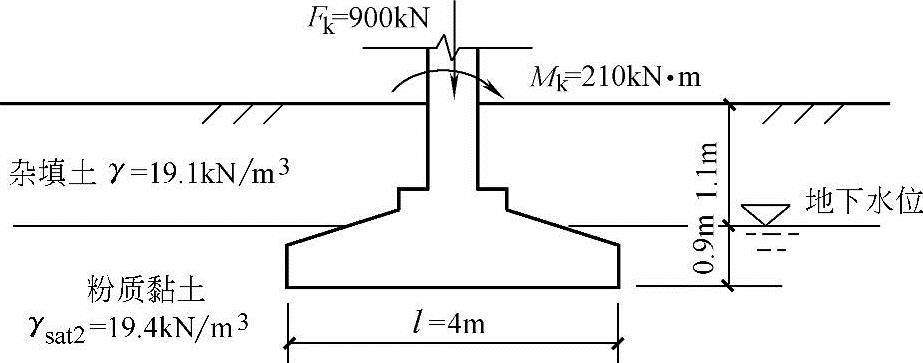
图5.3-4 【例5.3-10】~【例5.3-14】用图
Rk=Fk+Gk=Fk+20dA-10dwA=(900+20×2.0×4×3-10×0.9×4×3)kPa=1272kPa
弯矩为210kN·m,合力偏心距为

因为e=0.165m<(4/6)m=0.67m,所以分布为梯形,最大基底压力直接用式(5.3-4)计算
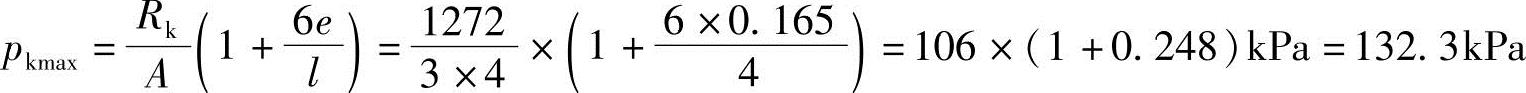
【例5.3-11】 试问基底压力标准值最小值与下列哪项数值最接近?
(A)48.8kPa (B)68.8kPa (C)79.7kPa (D)88.8kPa
答案:(C)
解答:最小基底压力标准值直接用式(5.3-4)计算
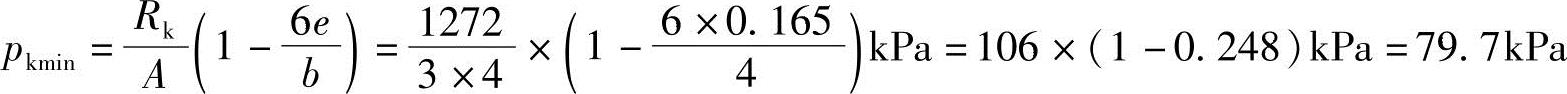
【例5.3-12】 基底压力的平均值和相应的基底附加压力与下列哪项数值最接近?
(A)106kPa,76.5kPa (B)75kPa,45.5kPa
(C)115kPa,85.5kPa (D)95kPa,65.5kPa
答案:(A)
解答: 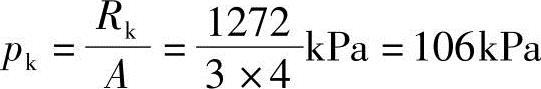
p0=pk-σcd=[106-(19.1×1.1+9.4×0.9)]kPa=(106-29.47)kPa=76.5kPa
【例5.3-13】 若作用弯矩标准值由210kN·m变为1050kN·m,试问基底压力标准值最大值与下列哪项数值最接近?
(A)206.3kPa (B)237.2kPa (C)240.0kPa (D)240.6kPa
答案:(D)
解答:作用在基础底面中心的总竖向力标准值为
Rk=Fk+Gk=Fk+20dA-10dwA=(900+20×2.0×4×3-10×0.9×4×3)kPa=1272kPa
弯矩为1050kN·m,合力偏心距为
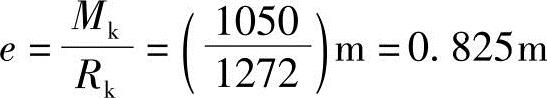
因为e=0.825m>(4/6)m=0.67m,所以分布将出现最小基底压力为负的情况,基底与地基土体之间不能承受拉力,所以会出现应力重分布现象。
矩形基础b=3m,l=4m,三角形分布的宽度范围为
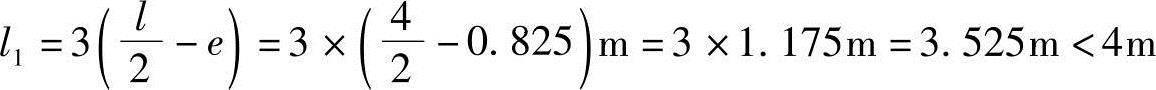
则最大基底压力标准值为
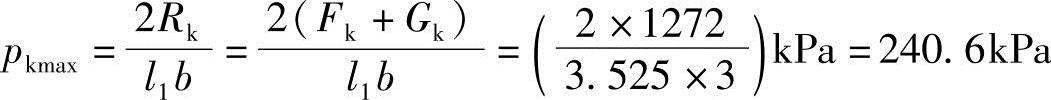
【例5.3-14】~【例5.3-16】 墙下条形基础宽为4.2m,如图5.3-5所示,作用在地面处和基础上端的竖向力标准值分别为640kN/m(中心荷载)和280kN/m(偏心距为0.5m),在地面处还作用了水平力标准值150kN/m,基础埋深为2.2m,地下水位在基底处,土层重度水上为18.2kN/m3,水下为18.7kN/m3。
【例5.3-14】 试问仅有两个竖向力Fk1和Fk2作用时,基底压力和基底附加压力最大值与下列哪项数值最接近?
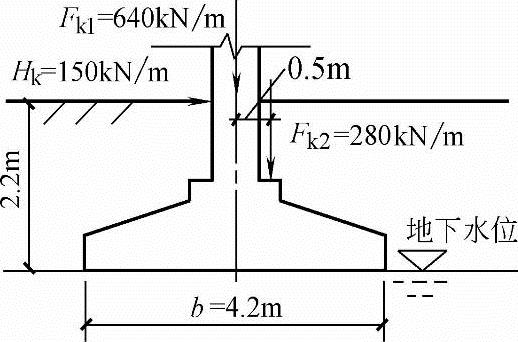
图5.3-5 【例5.3-14】~【例5.3-16】用图
(A)215.4kPa,196.3kPa (B)266.6kPa,226.6kPa
(C)288.7kPa,247.6kPa (D)310.6kPa,270.6kPa
答案:(D)
解答:作用在基础底面中心的总竖向力为
Rk=Fk1+Fk2+Gk=Fk1+Fk2+20db=(640+280+20×2.2×4.2)kN/m=1104.8kN/m
弯矩为
Mk=Fk2×0.5=(280×0.5)kN·m/m=140kN·m/m
合力偏心距为
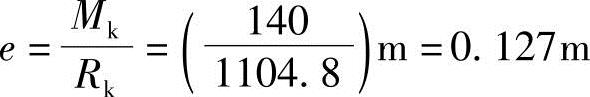
因为e=0.127m<(4.2/6)m=0.7m,所以基底压力分布呈梯形,用式(5.3-4)计算
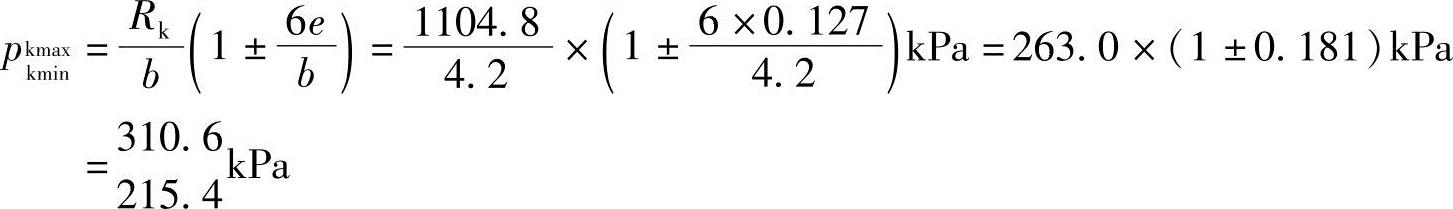
基底附加压力为
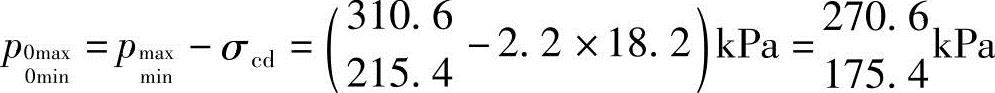
【例5.3-15】 在两个竖向力和一个水平力的共同作用下,且地下水位升至地面处,试问基底压力和基底附加压力最大值与下列哪项数值最接近?
(A)310.6kPa,291.46kPa (B)310.6kPa,292.6kPa
(C)422.6kPa,404.6kPa (D)400.8kPa,381.7kPa
答案:(D)
解答:作用在基础底面中心的总竖向力
Rk=Fk1+Fk2+Gk=Fk1+Fk2+(20-10)db=[640+280+(20-10)×2.2×4.2]kN/m
=1012.4kN/m
弯矩为
Mk=Fk2×0.5+Hk×2.2=(280×0.5+150×2.2)kN·m/m=(140+330)kN·m/m
=470kN·m/m
合力偏心距为
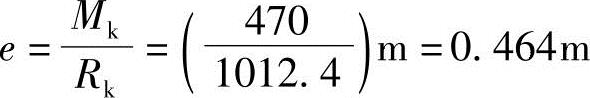
因为e=0.464m<(4.2/6)m=0.7m,所以基底压力分布呈梯形,用式(5.3-4)计算
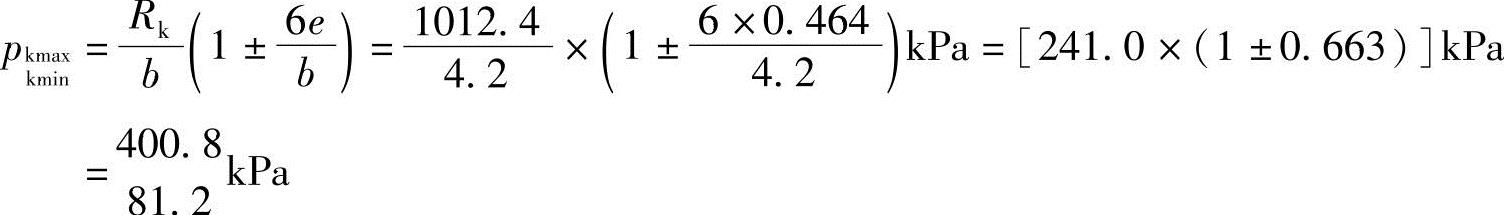
基底附加压力为
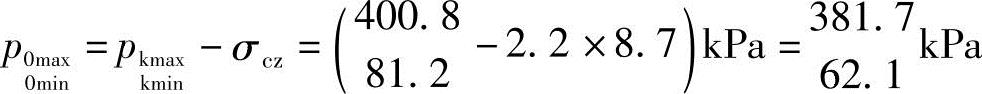
【例5.3-16】 在两个竖向力和一个水平力的共同作用下,地下水位在基底处,如果产生的基底压力最小值为零时需要将水平力标准值增加到下列哪项数值?
(A)229kPa (B)259kPa (C)288kPa (D)352kPa
答案:(C)
解答:作用在基础底面中心的总竖向力同【例5.3-14】
Rk=Fk1+Fk2+Gk=Fk1+Fk2+20db=(640+280+20×2.2×4.2)kN/m=1104.8kN/m
若要分布呈三角形,则偏心距e=(4.2/6)m=0.7m。
合力偏心距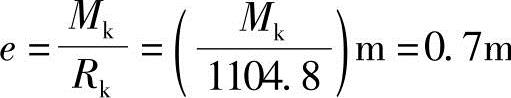 ,则Mk=(1104.8×0.7)kN·m/m=773.4kN·m/m。
,则Mk=(1104.8×0.7)kN·m/m=773.4kN·m/m。
弯矩为
Mk=Fk2×0.5+Hk×2.2=280×0.5+Hk×2.2=140+2.2Hk=773.4kN·m/m
则
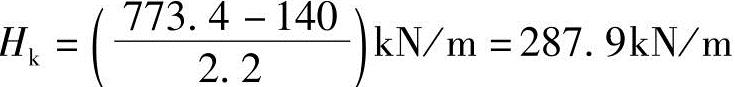
有关全国一、二级注册结构工程师专业考试教程的文章

心理学家艾丽娅·克拉姆和她的同事开发了压力思维模式测试,以评估人们对压力的看法。思维模式2:压力有促进作用。根据美国心理学协会的调查,多数人认为他们承受的压力水平不健康。克拉姆的研究表明,相信压力有促进作用的人,比那些认为压力有害的人,更少抑郁,对生活更满意。然而,克拉姆的研究表明,这些性格特点都无法解释压力思维模式对健康、幸福或者工作效率的影响。......
2024-01-19

引起人们工作压力的原因多种多样,理解这些压力因素和他们之间可能的相互作用很重要。导致压力的因素主要有两类:组织因素和个人因素。在美国,全国性调查显示大约25%的员工都遇到各种各样由压力引起的问题,几种组织因素是员工压力的主要源头。当前组织中的暴力水平是需要重视和处理的工作压力的一个重要来源。(二)导致压力与生活相关的因素员工的个人生活往往对日常工作有着显著影响。......
2023-08-02

而且应该把教育指导作为一个重要内容来完成,这种指导既要考虑普通教育的需要,也要考虑职业培训的需要,当然,杰出的人才不会因为没有顾问或权威人士指导而被埋没,教育指导也不会发现许多沉默寡言、蓬头垢面的弥尔顿,也不会将许多不受欢迎的济慈送进药学院去。然而如果一个人选择了不适合自己的路,教育指导也无能为力了。我们必须清楚,系统的教育就是学校教育。......
2023-08-09

但所有的压力源有一个共同特征:当个体认为压力源是某种超过个人反应能力的要求时,压力源便产生压力或潜在压力。也就是说,压力是人类神经系统对环境压力源作出的自然反应,然而,身体对压力源的反应能力是有限的。......
2023-08-02

此期间,压力荷尔蒙提升了脑部支持学习和记忆区域的活动。压力反应帮你应对挑战、与人联结、学习和成长压力反应如何帮你: 你怎么知道这正在发生应对挑战·集中注意力 你注意到心脏怦怦跳动、身体出·强化感觉 汗或者呼吸加快。然后阅读上页的总结“压力反应帮你应对挑战、与人联结、学习和成长”。......
2024-01-19

面对紧张的职场压力,该如何排解呢?下面介绍几招心理自救的方法,帮你摆脱职场压力。如果精神压力过大,心理承受能力有限,则需进行专门的心理疏导或治疗。譬如练习瑜伽和太极拳,对消除压力,缓解心血管疾病症状非常有利。根据研究,音乐治疗能够诱发生理反应,协助放松及调适压力,达到身心舒畅的目的。......
2023-08-08

表4.1给出了试验区岩体地应力的反演成果。根据表4.2绘制劈裂压力与裂缝长度关系见图4.9和图4.10。其可能原因是,连通性较好的长裂隙受地应力的作用相对较弱,产生劈裂所需的水压力相对较小。由此可见,劈裂压力理论值范围与压水试验得到的实验值范围吻合程度较高,说明理论计算值是合理的。......
2023-06-28

岩体的水力劈裂现象通常指岩体在高压水作用下,流量产生突然增加的现象。图4.7表明1号试验孔断层段在中速法第一次高压压水条件下发生了三次较大规模的水力劈裂现象,第一次劈裂时的压力为3.0MPa,第二次劈裂时的压力为5.5MPa,第三次劈裂时的压力为6.5MPa。......
2023-06-28
相关推荐