自重应力的定义及计算方法

2025-09-30 理论教育版权反馈

【摘要】：自重应力是土体在自身重量作用下变形稳定以后的有效应力。通常自重应力不会引起土层的变形，但对于新填土或欠固结土，在自重作用下尚未固结稳定，需要考虑土的自重引起的变形。若地下水位在41m高程处，细砂层底层处竖向自重应力σcz与下列哪项数值最接近？

自重应力是土体在自身重量作用下变形稳定以后的有效应力。在地面水平的情况下，土体在自重作用下无侧向变形和剪切变形，只有竖向变形，这种条件称为无侧向变形条件或侧限条件或K₀条件。

1.竖向自重应力

利用有效应力原理，地面下深度为z处的土层竖向自重应力，等于该处单位面积上土柱的有效重量，按下式计算

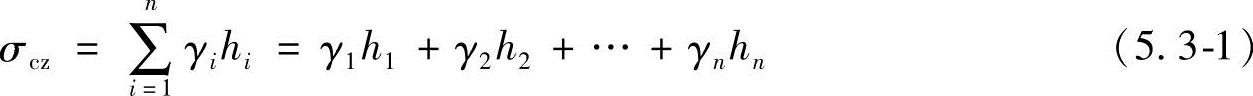
式中 γ_i——第i层土的天然重度（kN/m³），一般土层地下水位以下采用浮重度γ′，对于下层土层为不透水且土层处于地下水位以下的情况，也可采用饱和重度计算；

h_i——第i层土层的厚度（m）；

n——从地面到深度z处的土层数。

可见，竖向自重应力沿深度呈线性分布，在土层的分界面处有转折，且土层越深自重应力越大，如图5.3-1a所示。通常自重应力不会引起土层的变形，但对于新填土或欠固结土，在自重作用下尚未固结稳定，需要考虑土的自重引起的变形。

2.侧向自重应力

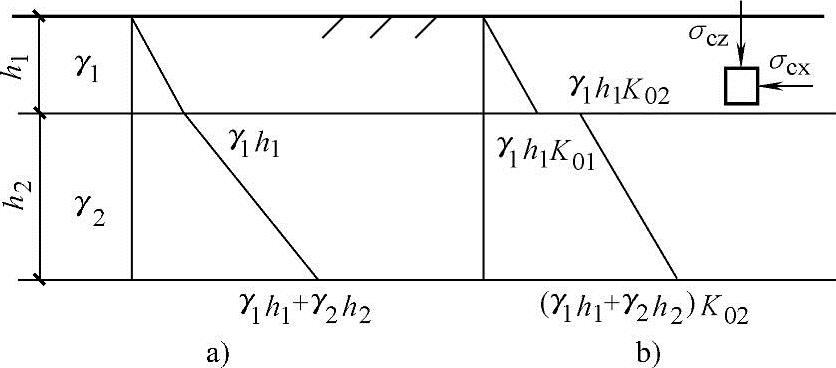
图5.3-1 自重应力分布图

a）σ_cz分布 b）σ_cx分布

侧向自重应力可按式（5.3-2）由竖向自重应力计算

式中 K_0j——j点土的静止侧压力系数，可由试验确定，或采用经验公式：K₀≈1-sinφ′，其中φ′为土的有效内摩擦角。

其分布如图5.3-1b所示，在土层的分界面处有突变。

【例5.3-1】～【例5.3-3】图5.3-2所示资料中细砂层下部为透水层。

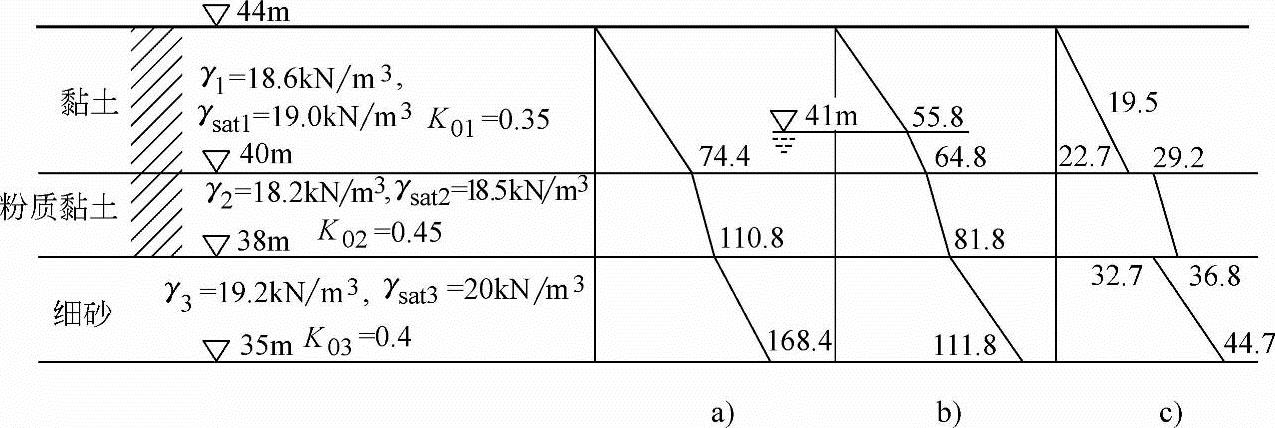
图5.3-2 【例5.3-1】～【例5.3-3】用图(https://www.chuimin.cn)

【例5.3-1】若地下水位很深，细砂层底层处竖向自重应力σ_cz与下列哪项数值最接近？画出分布图。

（A）83.0kPa （B）168.4kPa （C）173.0kPa （D）111.8kPa

答案：（B）

解答：

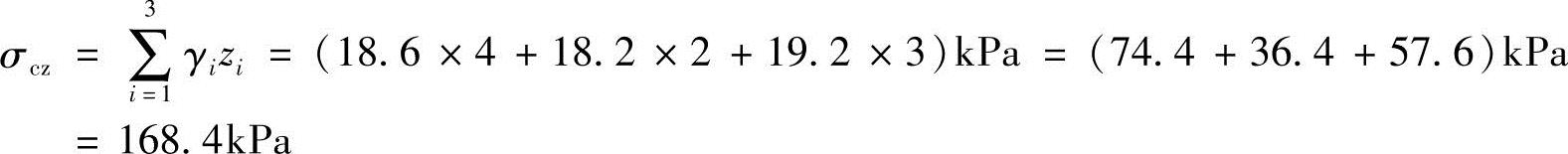
分布图如图5.3-2a所示。

【例5.3-2】若地下水位在41m高程处，细砂层底层处竖向自重应力σ_cz与下列哪项数值最接近？画出分布图。

（A）83.0kPa （B）168.4kPa （C）173.0kPa （D）111.8kPa

答案：（D）

解答：

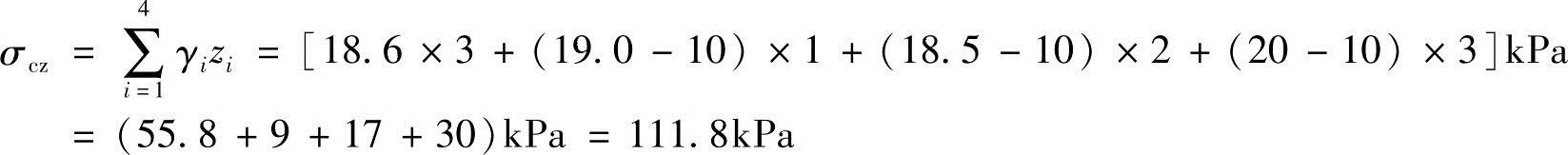
分布图如图5.3-2b所示。

【例5.3-3】若地下水位在41m高程处，细砂层底层处侧向自重应力σ_cx与下列哪项数值最接近？画出分布图。

（A）39.1kPa （B）44.7kPa （C）50.3kPa （D）67kPa

答案：（B）

解答：

σ_cx=K₀₃σ_cz=（0.4×111.8）kPa=44.7kPa

分布图如图5.3-2c所示。