连接件的安装是确保安装质量的重要环节。该部分的工作包括连接件的处理,无预埋件的增补穿墙螺栓或连接板等。2)广告牌固定在墙面上或立于地面上均需符合建筑安装的技术规范,连接的膨胀螺栓及预埋金属固定构件,必须能承受巨大质量框架的拉力,必要时要在单面、双面或三面多处用撑脚支撑广告牌,确保安全。......
2023-06-15
1.节点板在拉力、剪力作用下的强度
连接节点处板件在拉力、剪力作用下的强度应按下列公式计算:

式中 N——作用于板件上的拉力;
Ai——第i段破坏面的截面积,Ai=tli;当为螺栓(或铆钉)连接时,应取净截面面积;
t——板件厚度;
li——第i破坏段的长度,应取板件中最危险的破坏线的长度(图3.4-13);
ηi——第i段的拉、剪折算系数;
αi——第i段破坏线与拉力轴线的夹角。
2.桁架节点板按有效宽度法计算强度
桁架节点板(板件为轧制T形和双板焊接T形截面者除外)的强度除可按式(3.4-50)计算外,也可用有效宽度法按下式计算:

式中 be——板件的有效宽度(图3.4-14),当用螺栓(或铆钉)连接时,应减去孔径。
3.桁架节点板在斜腹杆压力作用下的稳定性计算

图3.4-13 板件的拉、剪撕裂
a)焊缝连接 b)螺栓(铆钉)连接 c)螺栓(铆钉)连接
(1)对有竖腹杆相连的节点板,当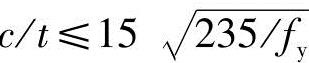 时(c为受压腹杆连接肢端面中点沿腹杆轴线方向至弦杆的净距离),可不计算稳定。否则按(3)中的方法计算稳定性。在任何情况下,c/t都不得大于
时(c为受压腹杆连接肢端面中点沿腹杆轴线方向至弦杆的净距离),可不计算稳定。否则按(3)中的方法计算稳定性。在任何情况下,c/t都不得大于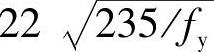 。
。
(2)对无竖腹杆相连的节点板,当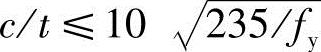 时,节点板的稳定承载力可取0.8betf。当
时,节点板的稳定承载力可取0.8betf。当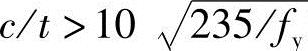 时,应按(3)中的方法计算稳定性。在任何情况下,c/t不得大于
时,应按(3)中的方法计算稳定性。在任何情况下,c/t不得大于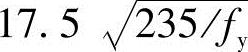 。
。
(3)桁架节点板在斜腹杆压力作用下的稳定计算
1)基本假定。在图3.4-15中,B-A-C-D为节点板失稳时的屈折线,其中 平行于弦杆,
平行于弦杆,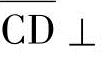
 。
。
在斜腹杆轴向压力N的作用下, A区(FBGHA板件)、
A区(FBGHA板件)、 区(AIJC板件)和
区(AIJC板件)和 区(CKMP板件)同时受压,当其中某一区先失稳后,其他区即相继失稳,为此要分别计算各区的稳定。
区(CKMP板件)同时受压,当其中某一区先失稳后,其他区即相继失稳,为此要分别计算各区的稳定。
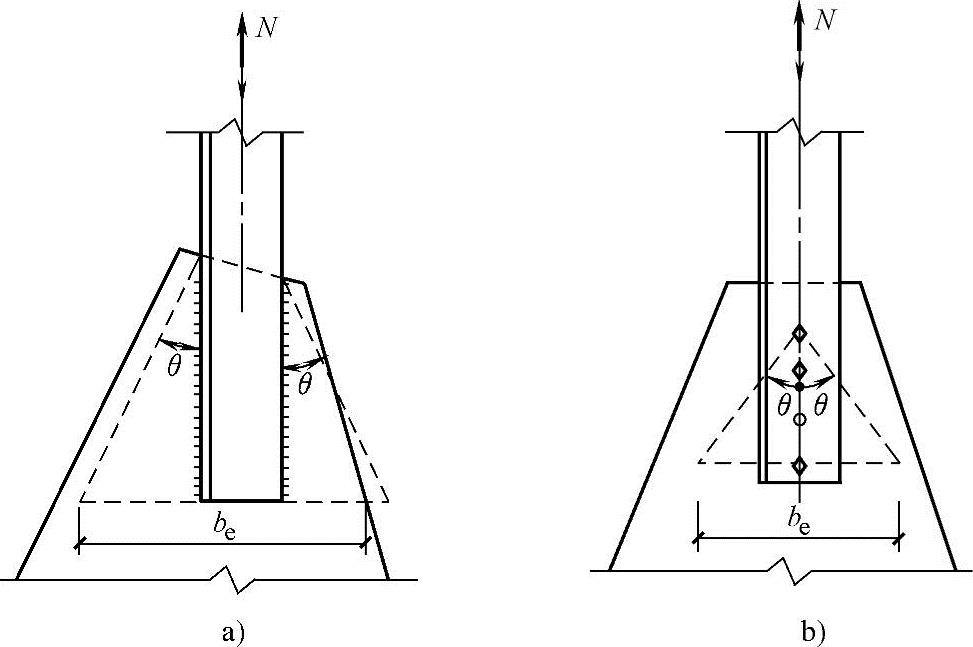
图3.4-14 板件的有效宽度(θ为应力扩散角,可取30°)
2)计算方法
 区:
区:
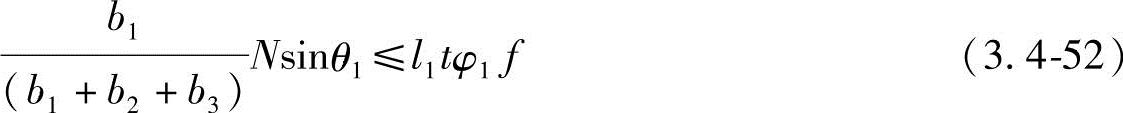
 区:
区:

 区
区
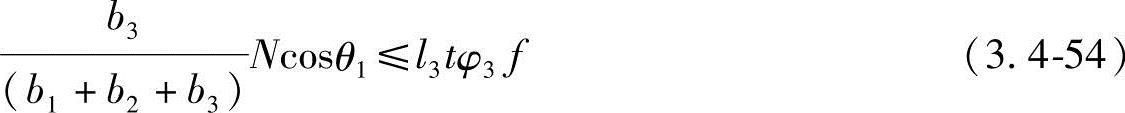
式中 t——节点板厚度;
N——受压斜腹杆的轴向力;
l1、l2、l3——屈折线 、
、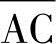 、
、 的长度;
的长度;
φ1、φ2、φ3——各受压区板件的轴心受压稳定系数,可按b类截面查取;其相应的长细比分别为

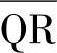 、
、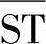 、
、 ——
—— 、
、 、
、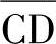 三区受压板件的中线长度,ST=c;
三区受压板件的中线长度,ST=c;
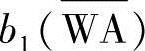 、
、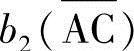 、
、 ——各屈折线段在有效宽度线上的投影长度。
——各屈折线段在有效宽度线上的投影长度。
对 且沿自由边加劲的无竖腹杆节点板(lf为节点板自由边的长度),亦可用上述方法进行计算,只是仅需验算
且沿自由边加劲的无竖腹杆节点板(lf为节点板自由边的长度),亦可用上述方法进行计算,只是仅需验算 区和
区和 区,而不必验算CD区。
区,而不必验算CD区。
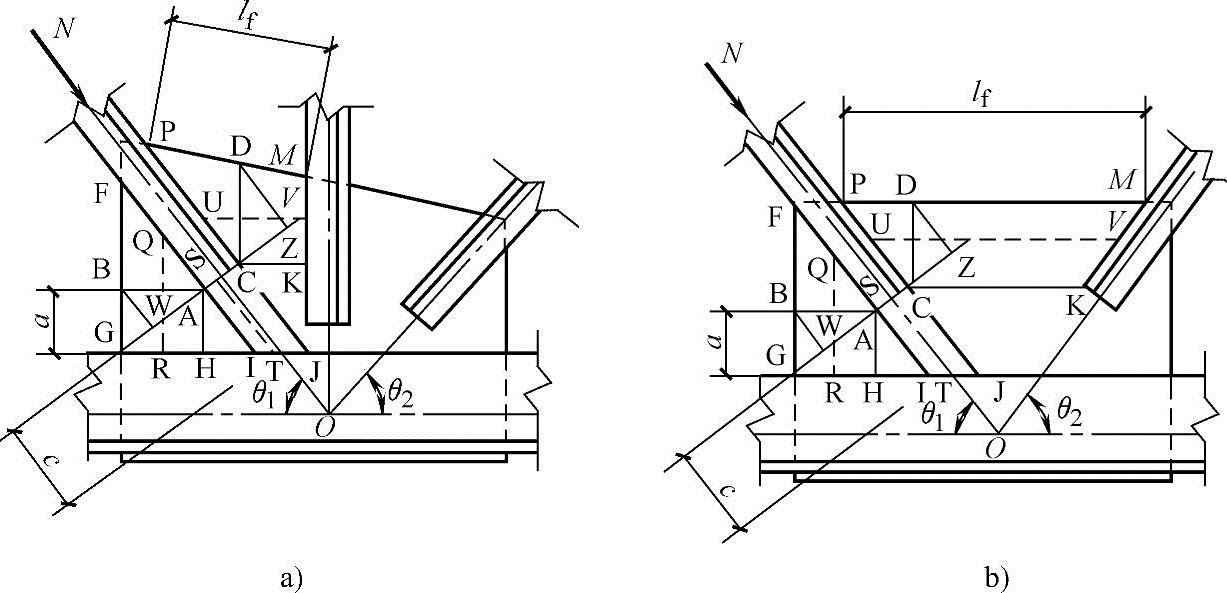
图3.4-15 节点板稳定计算简图
a)有竖杆时 b)无竖杆时
【例3.4-1】 关于螺栓连接,下列何项内容与《钢结构设计规范》(GB 50017—2003)要求不符?
(A)C级螺栓宜用于沿其杆轴方向受拉的连接
(B)对直接承受动力荷载的普通螺栓受拉连接,应采用双螺帽或其他能防止螺帽松动的有效措施
(C)螺栓中心间距最小容许距离为3d,d为螺栓直径
(D)每一杆件(缀条除外)在节点上以及拼接接头的一端,永久性的螺栓数不宜少于2个
答案:(C)
解答:由3.4.2节内容可知,(A)、(B)、(D)都是正确的。由表3.4-1可知,在(C)中的最小容许距离应为3d。
【例3.4-2】 试问,下列各种因素中哪种因素影响高强度螺栓的预拉力?
(A)连接表面的处理方法
(B)螺栓的性能等级及螺栓杆的直径
(C)构件的钢号
(D)荷载的作用方式
答案:(B)
解答:见表3.4-4。
【例3.4-3】 某厂房钢屋架下弦节点悬挂单轨吊车梁,吊车梁与钢屋架下弦节点间采用普通C级螺栓连接,如图3.4-16所示。若已知悬吊点竖向荷载设计值取N=42.1kN,试问,连接螺栓的公称直径按计算应选用下列何项规格最为合适?
(A)2M14 (B)2M16 (C)2M18 (D)2M20
答案:(B)
解答:按式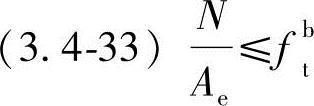 。查表3.1-4C级螺栓fbt=170N/mm2
。查表3.1-4C级螺栓fbt=170N/mm2

查表:2M16 An=2×157=314mm2(可)
(2M14 An=2×115=230<247.6mm2)
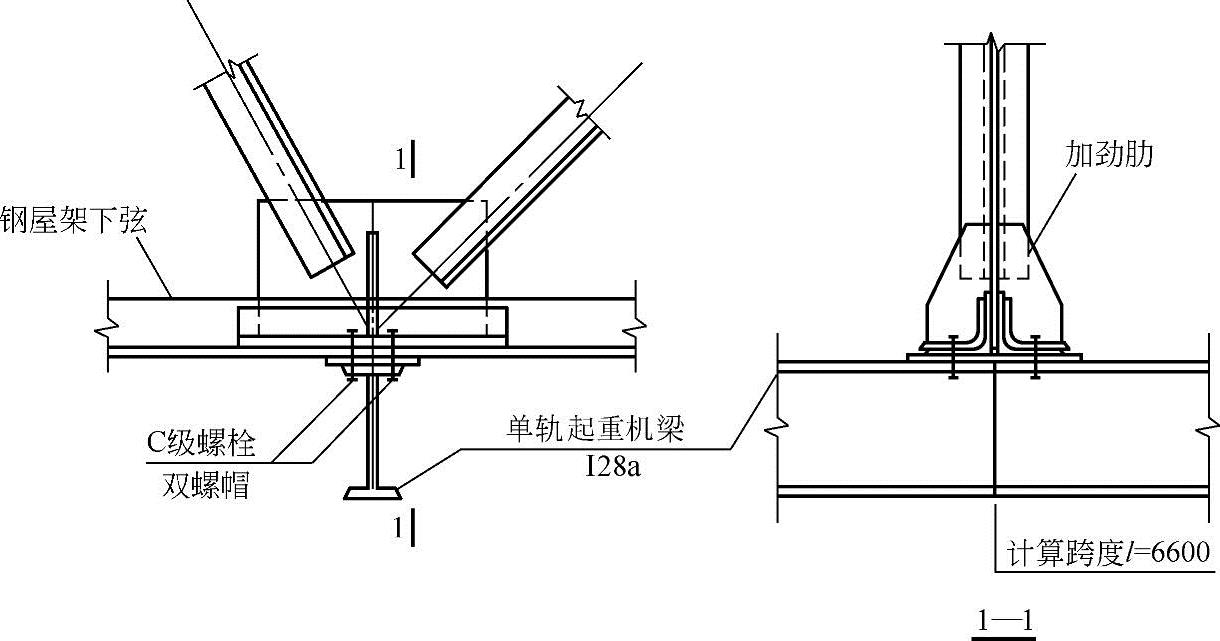
图 3.4-16
【例3.4-4】 图3.4-17所示工字形截面牛腿与柱翼缘焊接。焊缝为对接焊缝,手工电弧焊,无引弧板,焊缝质量为三级,焊条为E43型。构件钢材为Q235。焊缝有效截面形心O处作用有竖向力V=250kN,弯矩M=75kN·m。假设弯矩由全焊缝承担,竖向力V由腹板焊缝承担,则“1”点处焊缝的折算应力(N/mm2)与下列何项数值最为接近?
(A)145 (B)186
(C)184 (D)205
答案:(C)
解答:焊缝截面与牛腿截面相同。由于施焊时无引弧板,故在计算时应将每条焊缝的两端各减去焊缝的厚度(板件的厚度)。
焊缝有效截面惯性矩:
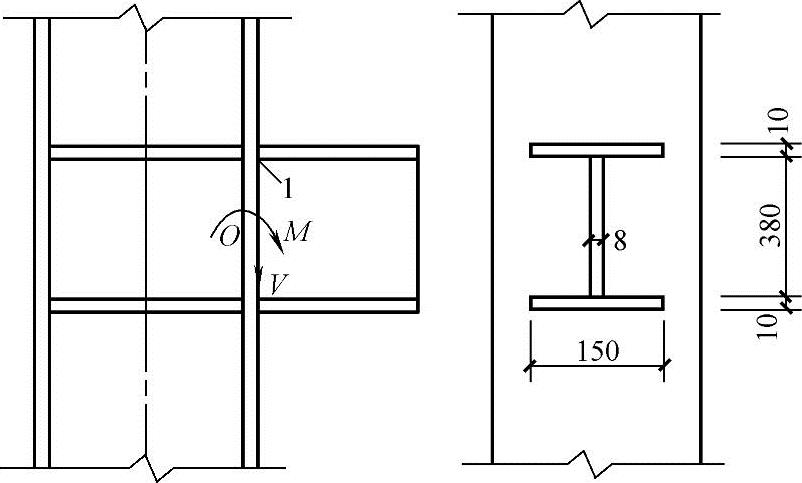
图3.4-17 工字形截面对接焊缝

腹板焊缝有效截面面积:

【例3.4-5】 梯形屋架下弦某一节点如图3.4-18所示。腹杆AD截面为2 100×8,承受的轴心压力N=388.2kN。节点板厚度t=12mm。
100×8,承受的轴心压力N=388.2kN。节点板厚度t=12mm。
腹杆AD与节点板采用侧面角焊缝连接,角钢肢背焊缝的焊脚尺寸为hf1,角钢肢尖焊缝的焊脚尺寸为hf2,则取下列哪一组焊脚尺寸最为合适?
(A)hf1=10mm,hf2=6mm
(B)hf1=10mm,hf2=8mm
(C)hf1=8mm,hf2=8mm
(D)hf1=8mm,hf2=6mm
答案:(D)
解答:根据3.4.1节:
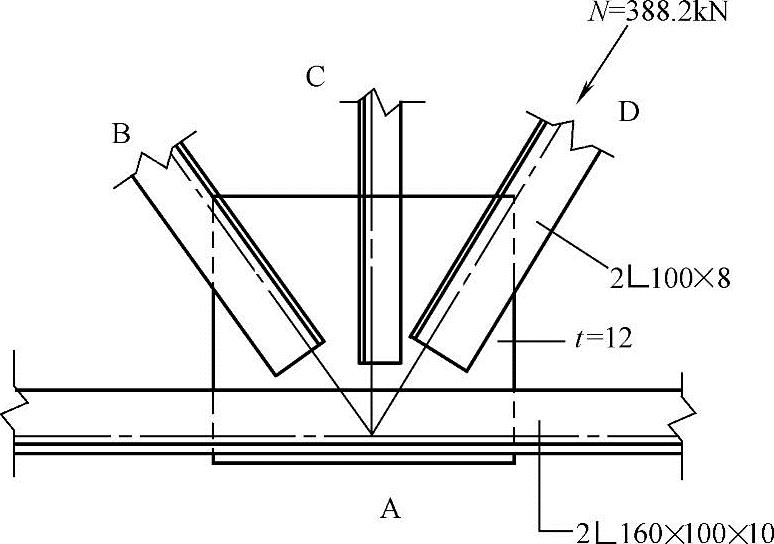
图3.4-18 屋架下弦节点
角钢肢背、肢尖焊缝焊脚尺寸最小值: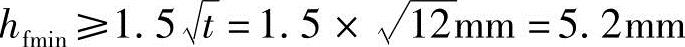
角钢肢背焊缝焊脚尺寸最大值:hf1max≤1.2t=1.2×8mm=9.6mm
角钢肢尖焊缝焊脚尺寸最大值:hf2max≤t-(1~2)=8-(1~2)=6~7mm
【例3.4-6】 屋架腹杆角钢型号及受力同【例3.4-5】。如果角钢肢背、肢尖焊缝的焊脚尺寸均取hf=6mm,则角钢肢背所需的焊缝长度(l′w1)、肢尖所需要的焊缝长度(l′w2)与下列哪组最接近?
(A)lw′1取240mm,lw′2取90mm (B)lw′1取220mm,lw′2取100mm
(C)lw′1取100mm,lw′2取200mm (D)lw′1取100mm,lw′2取100mm
答案:(B)
解答:根据3.4.3节:
肢背焊缝受力:N1=k1N=0.7×388.2kN=271.74kN
肢尖焊缝受力:N2=k2N=0.3×388.2kN=116.46kN
肢背焊缝计算长度: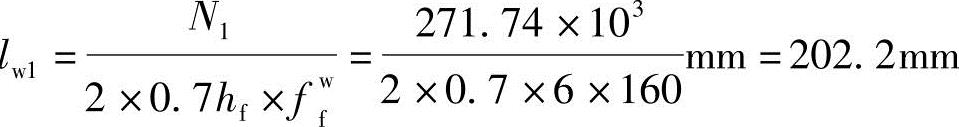
肢背焊缝实际长度:lw′1=lw1+2hf=(202.2+2×6)mm=214.2mm,取220mm
肢尖焊缝计算长度: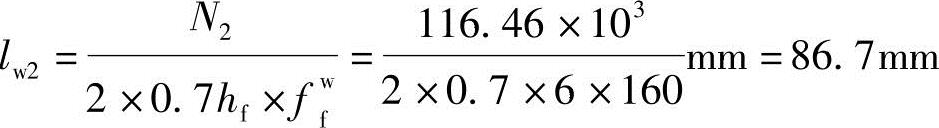
肢尖焊缝实际长度:lw′2=lw2+2hf=(86.7+2×6)mm=98.7mm,取100mm
【例3.4-7】 图3.4-19所示牛腿与柱翼缘采用角焊缝连接。牛腿上作用有竖向力设计值(静力荷载)F=330kN,焊缝焊脚尺寸hf=8mm。剪力由腹板焊缝平均承担。
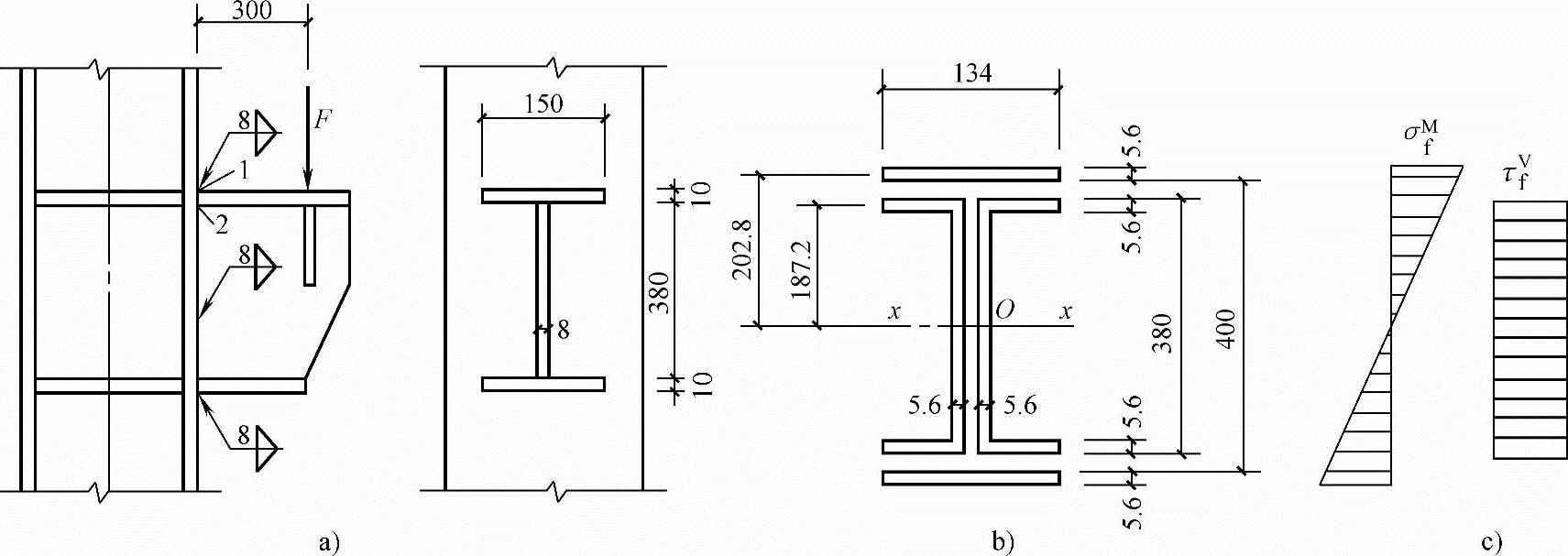
图3.4-19 【例3.4-7】图
a)牛腿与柱连接 b)焊缝有效截面 c)焊缝有效截面上应力分布
“1”点和“2”点处焊缝的应力(N/mm2)与下列哪一组数值最接近?
(A)128.8,124.6 (B)120.8,124.6
(C)128.8,120.8 (D)120.8,120.8
答案:(A)
解答:
将每条焊缝两端各减去hf得到焊缝的计算长度,进一步得到焊缝的有效截面和有效截面形心O(图3.4-19b)。将外力F简化至焊缝有效截面形心O后形成作用在O处的竖向剪力V和弯矩M。
V=F=330kN
M=Fe=330×0.3kN·m=99kN·m
he=0.7hf=0.7×8mm=5.6mm
全部焊缝有效截面对x轴的惯性矩:
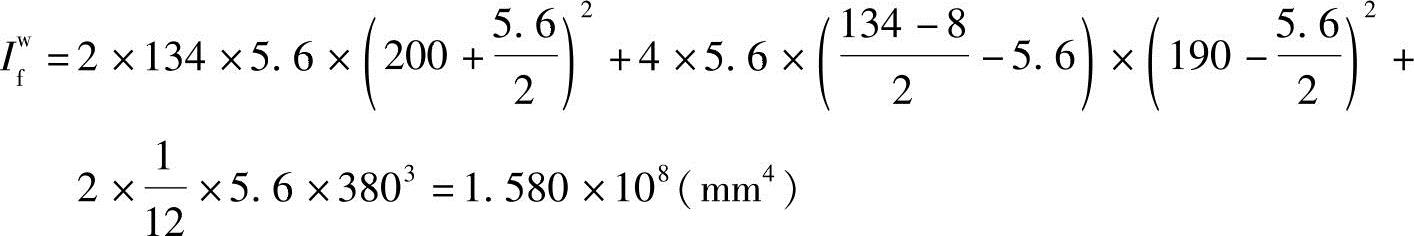
腹板焊缝有效截面面积:
Awf=2×5.6×380mm2=4256mm2
“1”点处焊缝应力:
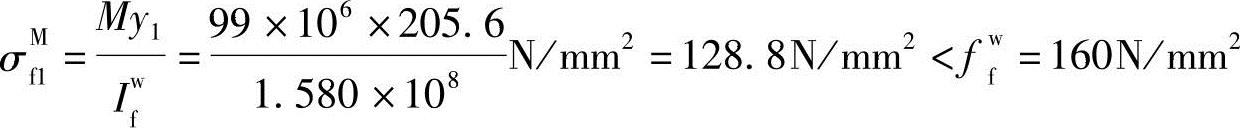
“2”点处焊缝应力:
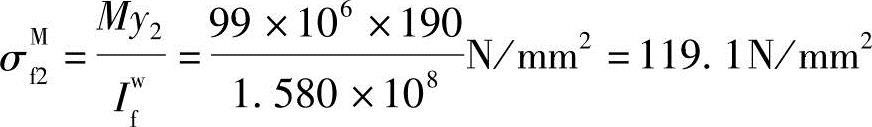
剪力由腹板焊缝平均承担:
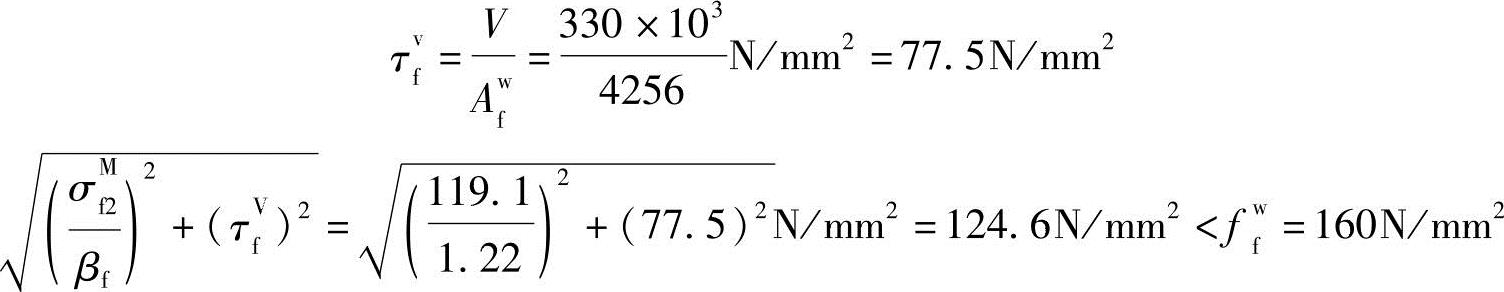
【例3.4-8】 图3.4-20所示钢板拼接连接,连接螺栓为4.6级普通C级螺栓,螺栓直径d=20mm,螺栓孔直径d0=21.5mm。钢板钢材为Q235。此连接所能承受的最大轴心拉力设计值(kN)与下列何项最为接近?
(A)945.1 (B)1134.2 (C)1506.4 (D)1579.2
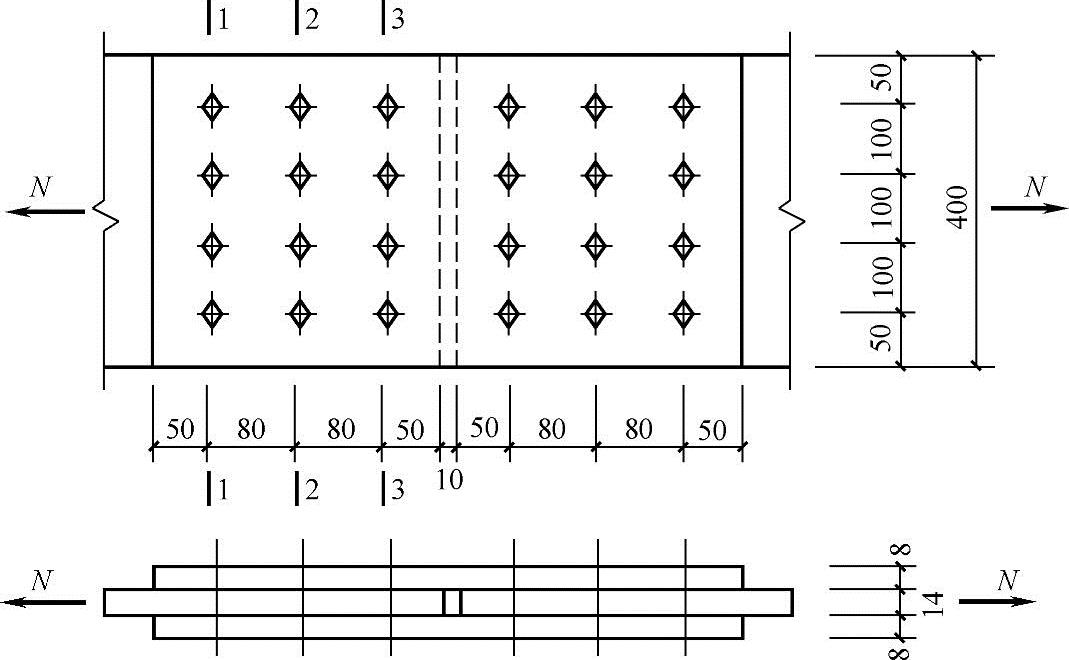
图3.4-20 板件拼接
答案:(A)
解答:
查表3.1-4:fbv=140N/mm2,fbc=305N/mm2
查表3.1-1:钢材的强度设计值f=215N/mm2
螺栓承载力:
沿内力方向最外排螺栓中心间距离为160mm<15d0=15×21.5mm=322.5mm,螺栓的承载力不需要折减。

板件净截面承载力(1—1截面):
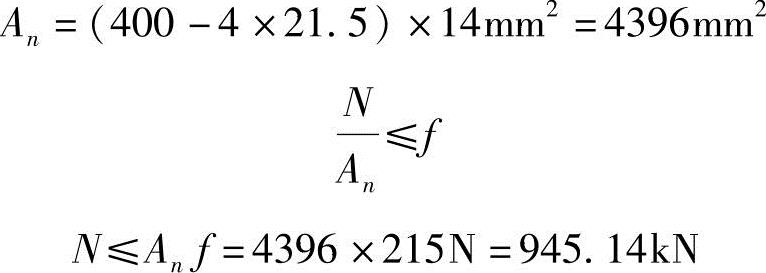
盖板:盖板厚度之和大于被连接板件厚度,且螺栓排列规则,盖板的净截面承载力大于板件的净截面承载力。
所以连接所能承受的最大轴心拉力设计值为945.14kN。
【例3.4-9】 图3.4-20所示钢板拼接连接,连接螺栓为10.9级高强度螺栓摩擦型连接,构件表面采用喷砂处理,螺栓直径d=20mm,螺栓孔直径d0=21.5mm。钢板钢材为Q235。此连接所能承受的最大轴心拉力设计值(kN)与下列何项最为接近?
(A)945.1 (B)1134.2 (C)1506.4 (D)1579.2
答案:(B)
解答:
查表3.4-3、表3.4-4:μ=0.45,P=155kN
螺栓承载力:
Nbv=0.9nfμP=0.9×2×0.45×155kN=125.55kN
N=12Nbv=12×125.55kN=1506.6kN
板件净截面承载力(1—1截面):
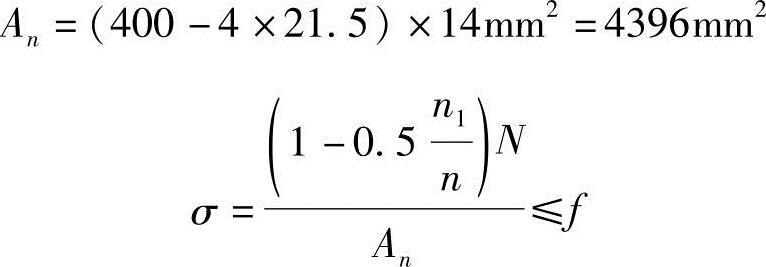

板件毛截面承载力:
A=400×14mm2=5600mm2
N≤Af=5600×215N=1204.0kN
盖板:盖板厚度之和大于被连接板件厚度,盖板的承载力大于板件的承载力。
所以连接所能承受的最大轴心拉力设计值为1134.17kN。
【例3.4-10】 图3.4-20所示钢板拼接连接,连接螺栓为10.9级高强度螺栓承压型连接,螺栓直径d=20mm,螺栓孔直径d0=21.5mm,螺纹处有效直径de=17.65mm,假设剪切面在螺纹处,钢板钢材为Q235。此连接所能承受的最大轴心拉力设计值(kN)与下列何项最为接近?
(A)945.1 (B)1134.2 (C)1506.4 (D)1579.2
答案:(A)
解答:
查表3.1-4:fbv=310N/mm2,fbc=470N/mm2
查表3.1-1:钢材的强度设计值f=215N/mm2
螺栓承载力:
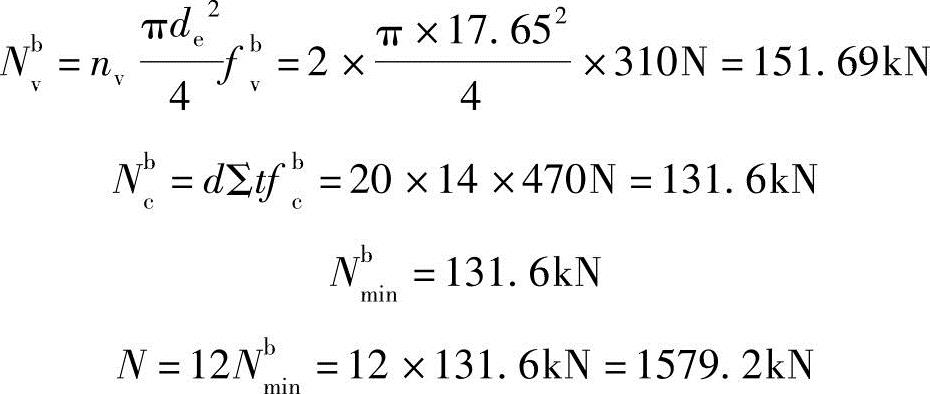
板件净截面承载力(1—1截面):
An=(400-4×21.5)×14mm2=4396mm2
N≤Anf=4396×215N=945.14kN
盖板:盖板厚度之和大于被连接板件厚度,且螺栓排列规则,盖板的净截面承载力大于板件的净截面承载力。
所以连接所能承受的最大轴心拉力设计值为945.14kN。
【例3.4-11】 如图3.4-21a所示,牛腿用连接角钢2 100×20及M22螺栓(4.6级普通C级螺栓)和柱连接。F=200kN,板件(构件)钢材为Q235,螺栓螺纹处有效截面面积Ae=303.4mm2。分别分析与柱翼缘连接肢上的螺栓和与牛腿板连接肢上的螺栓是否满足受力要求。
100×20及M22螺栓(4.6级普通C级螺栓)和柱连接。F=200kN,板件(构件)钢材为Q235,螺栓螺纹处有效截面面积Ae=303.4mm2。分别分析与柱翼缘连接肢上的螺栓和与牛腿板连接肢上的螺栓是否满足受力要求。
解答:
1.与柱翼缘连接肢上的螺栓
查表3.1-4:fbv=140N/mm2,fbc=305N/mm2,fbt=170N/mm2
与柱翼缘连接肢上的螺栓为拉剪螺栓。外力简化至螺栓群形心后,在形心处形成竖向剪力V和弯矩M。弯矩作用下螺栓受力如图3.4-21b所示。
V=F=200kN
M=Fe=200×0.2kN·m=40kN·m
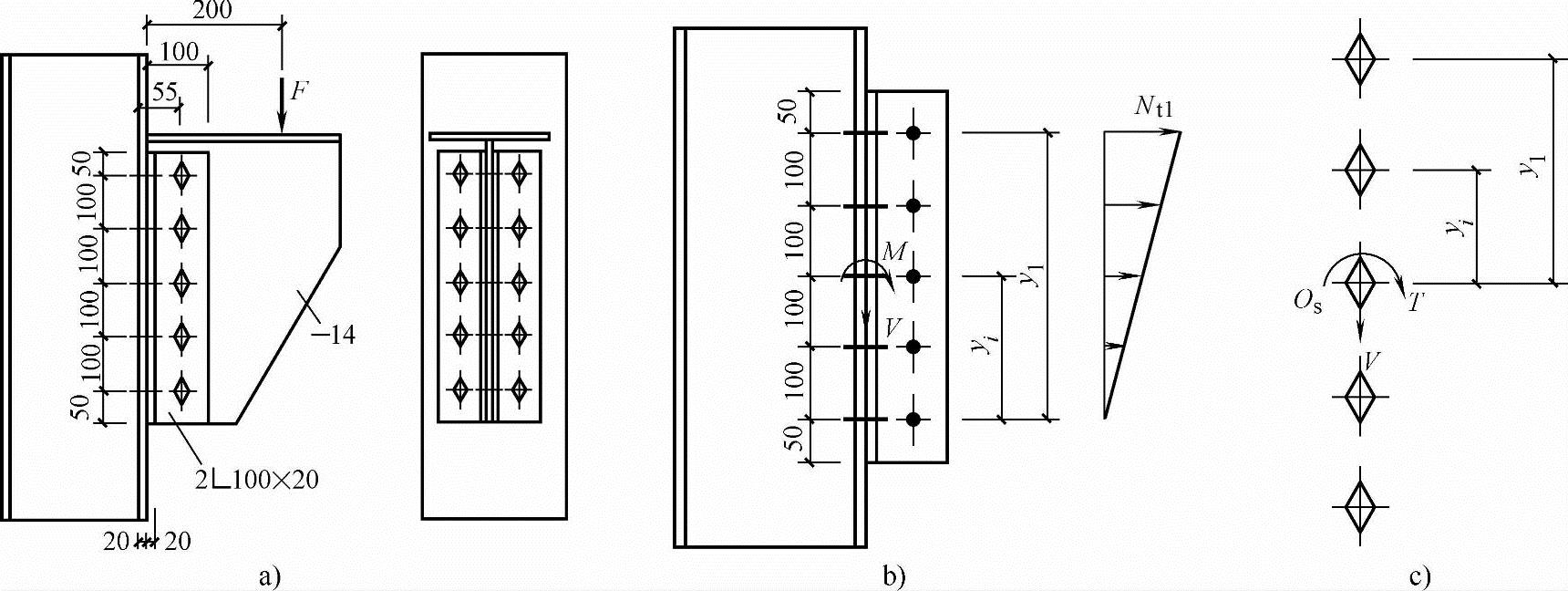
图3.4-21 T形截面牛腿与柱
a)牛腿与柱的连接 b)弯矩作用下与柱翼缘连接肢上的螺栓受力 c)扭矩作用下与牛腿板连接肢上的螺栓受力
第1排(最上面一排)螺栓受力最大:

2.与牛腿板连接肢上的螺栓
此连接处螺栓偏心受剪。偏心力F简化至螺栓群形心Os后,在形心Os处形成竖向剪力V和扭矩T(3.4-21c)。
V=F=200kN
T=Fe1=200×(0.2+0.02-0.055)kN·m
=200×0.165kN·m=33kN·m
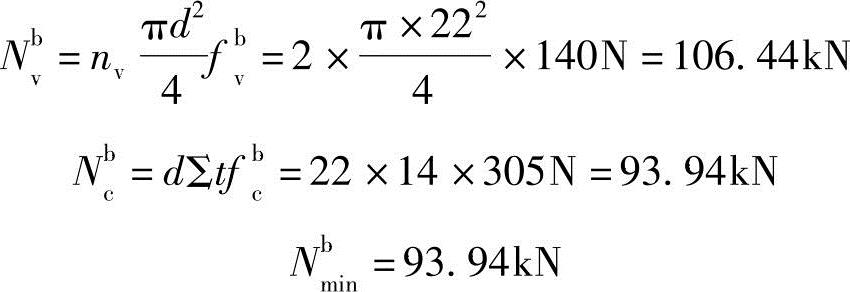
V在螺栓上产生的剪力:
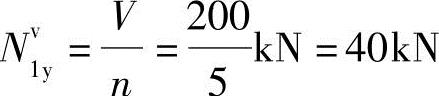
T在螺栓上产生的剪力:
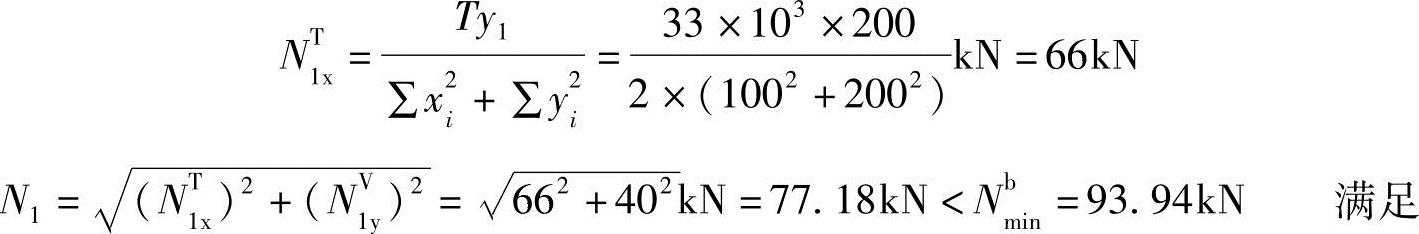
【例3.4-12】 螺栓布置及构件、板件尺寸如图3.4-21a所示。连接采用高强度螺栓摩擦型连接。螺栓为M22,8.8级,接触面采用喷砂处理。F=200kN,板件(构件)钢材为Q235。分别分析与柱翼缘连接肢上的螺栓和与牛腿板连接肢上的螺栓是否满足受力要求。
解答:查表3.4-3和表3.4-4:μ=0.45,P=150kN
1.与柱翼缘连接肢上的螺栓
Nbt=0.8P=0.8×150kN=120kN
Nbv=0.9nfμP=0.9×1×0.45×150kN=60.75kN
V=F=200kN
M=Fe=200×0.2kN·m=40kN·m
第1排(最上面一排)螺栓受力最大:
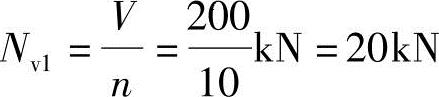
弯矩作用下螺栓受力如图3.4-22所示。
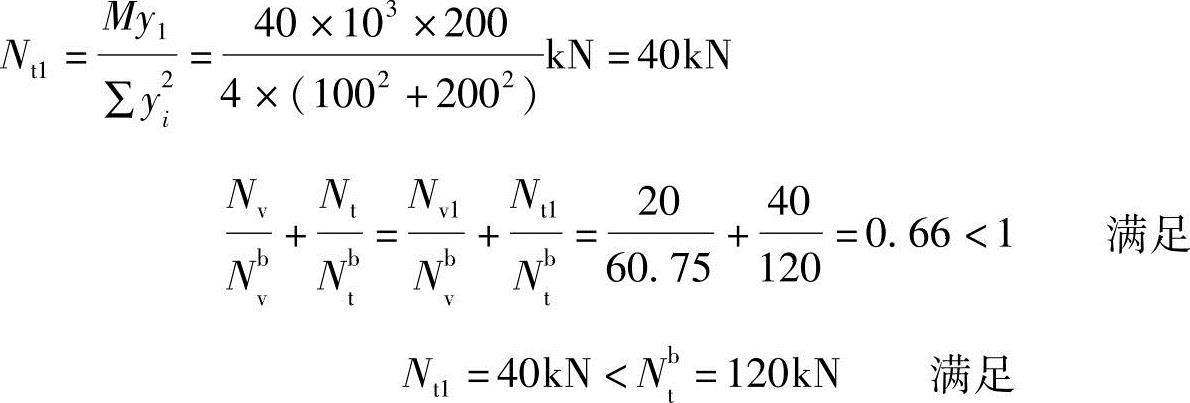

图3.4-22 弯矩作用下与柱翼缘连接肢上的螺栓受力
2.与牛腿板连接肢上的螺栓
此连接处螺栓偏心受剪。偏心力F简化至螺栓群形心Os后,在形心Os处形成竖向剪力V和扭矩T(图3.4-21c)。
V=F=200kN

【例3.4-13】 螺栓布置及构件、板件尺寸如图3.4-21a所示。连接采用高强度螺栓承压型连接。螺栓为M22,8.8级,螺纹处有效截面面积Ae=303.4mm2。F=200kN,板件(构件)钢材为Q235。分别分析与柱翼缘连接肢上的螺栓和与牛腿板连接肢上的螺栓是否满足受力要求。
解答:
1.与柱翼缘连接肢上的螺栓
查表3.1-4:fbv=250N/mm2,fbc=470N/mm2,fbt=400N/mm2

2.与牛腿板连接肢上的螺栓

V在螺栓上产生的剪力:

扭矩产生的剪力:
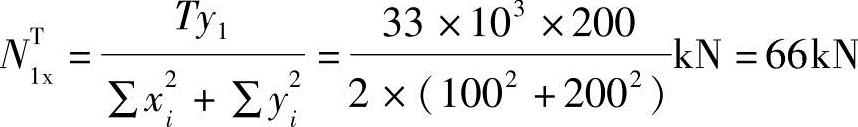

有关全国一、二级注册结构工程师专业考试教程的文章

连接件的安装是确保安装质量的重要环节。该部分的工作包括连接件的处理,无预埋件的增补穿墙螺栓或连接板等。2)广告牌固定在墙面上或立于地面上均需符合建筑安装的技术规范,连接的膨胀螺栓及预埋金属固定构件,必须能承受巨大质量框架的拉力,必要时要在单面、双面或三面多处用撑脚支撑广告牌,确保安全。......
2023-06-15

添加连接元件的方法与添加固定元件大致相同,首先选择下拉菜单命令并打开一个元件,系统会弹出图9.2.1所示的“元件放置”操控板,在操控板的“约束集”列表框中,可看到系统提供了多种“连接”类型,各种连接类型允许不同的运动自由度,每种连接类型都与一组预定义的放置约束相关联。图9.2.1 “元件放置”操控板向装配件中添加连接元件与添加固定元件的不同之处:● 向装配件中添加连接元件时,定义的放置约束为不完全约束模型。......
2023-06-20

装配式整体预应力板柱框架结构其预制楼板为方形或长方形。南京审计学院国际学术交流中心采用了预制柱、预制预应力混凝土叠合梁、叠合板的全装配框架结构形式,主体工程造价比现浇框架结构降低了10%左右。......
2023-10-12

因该制件年产量大,经分析采用多工位级进模冲压较为合理。图7-8 连接板图7-9 排样图3.模具结构设计连接板多工位级进模结构如图7-10所示。其结构特点如下:图7-10 连接板多工位级进模结构1—下模座 2—凹模 3—导料板 4—定位销 5—卸料板 6—卸料螺钉 7—凸模固定板 8—垫板 9—橡胶 10—落料凸模 11—大孔圆凸模 12—小孔圆凸模 13—活动导料销 14—弹簧 15—承料板1)该模具采用中间滑动导柱模架制造。......
2023-06-26

图8-20合并单元定义合并单元按照功能可分为间隔合并单元和母线合并单元。间隔合并单元用于线路或变压器的间隔合并单元,发送一个间隔的电气量数据。通过RP1285/RP1286或RP1296板件上的FT3接口或SMV9-2接口接收来自母线合并单元的数据,并完成切换功能。NSR-386A 间隔合并单元的前面板如图8-21 所示。合并单元通过 RP1296 采集电子式互感器输入电压。......
2023-06-28

螺纹连接是利用螺纹零件构成的可拆连接,应用十分广泛。表5-15螺纹连接的基本类型及应用续表续表常用螺纹连接件在机械制造中常见的螺纹连接件有螺栓、双头螺柱、螺钉、紧定螺钉、螺母和垫圈等。表5-16常用螺纹连接件的类型、结构特点及应用续表根据国家标准规定,螺纹连接件分为三个精度等级,其代号为A、B、C 级。③双头螺柱的轴心线必须与被连接件的表面垂直。......
2023-06-26

若采用单工序模,生产率低,制件精度无法保证,不能满足生产需求,故选用多工位级进模生产。图7-75 排样图3.模具结构设计连接板多工位级进模结构如图7-76所示。......
2023-06-26

利用SpaceClaim,用户可以比以往任何时候更快地进行模型的创建和编辑。SpaceClaim作为3D建模解决方案,日前其第四代产品已推出,即SpaceClaim Engineer和SpaceClaim Style。SpaceClaim使得设计和工程团队能更好地协同工作,能降低项目成本并加速产品上市周期。从图2-124可以看出,ANSYS SpaceClaim平台界面由以下几部分组成。图2-125 “文件”菜单图2-126 “打开”对话框SpaceClaim选项中可以对ANSYS SpaceClaim平台中的网格尺寸、渲染程度及保存格式等进行设置。......
2023-10-20
相关推荐