首页理论教育焊缝连接计算方法-全国一、二级注册结构工程师专业考试教程

焊缝连接计算方法-全国一、二级注册结构工程师专业考试教程

2023-08-28 理论教育版权反馈

【摘要】：工字形截面对接焊缝在弯矩和剪力共同作用下，除按式和式验算最大正应力和最大剪应力外，对受有较大正应力σ1和较大剪应力τ1处还应按下式验算折算应力：图3.4-2 工字形截面对接焊缝式中 σ1——腹板与翼缘连接处焊缝的正应力，；τ1——腹板与翼缘连接处焊缝的剪应力，；Sw1——焊缝截面计算剪应力处以上部分对中和轴的面积矩；tw——腹板厚度。式是焊缝计算的基本公式，在不同的受力状态下公式的形式可作相应的改变。

1.对接焊缝计算

（1）轴心力作用下对接焊缝的计算在对接接头和T形接头中，垂直于轴心力的对接焊缝或对接与角接组合焊缝，其强度按下式计算：

式中 N——轴心拉力或轴心压力；

t——对接接头中为连接件的较小厚度；在T形接头中为腹板的厚度；

l_w——焊缝计算长度。当焊缝无引弧板和引出板时，每条焊缝的计算长度取实际长度减去2t；当焊缝有引弧板和引出板时，每条焊缝的计算长度取实际长度；

f^w_t、f^w_c——对接焊缝的抗拉、抗压强度设计值，按表3.1-3选用。

当承受轴心力的板件用斜焊缝对接，焊缝与作用力间的夹角θ满足tanθ≤1.5时，对接焊缝的强度即可认为不低于焊件钢材的强度，不必再计算焊缝的强度。

（2）弯矩和剪力共同作用时的对接焊缝或对接与角接组合焊缝的计算

1）矩形截面（图3.4-1）

矩形截面对接接头受到弯矩和剪力的共同作用时，焊缝中的最大正应力和最大剪应力应分别符合下列公式的要求：

式中 I_w——焊缝截面的惯性矩；

W_w——焊缝截面模量；

S_w——焊缝截面计算剪应力处以上部分对中和轴的面积矩；

t——板厚；

f^w_v——对接焊缝抗剪强度设计值，按表3.1-3选用。

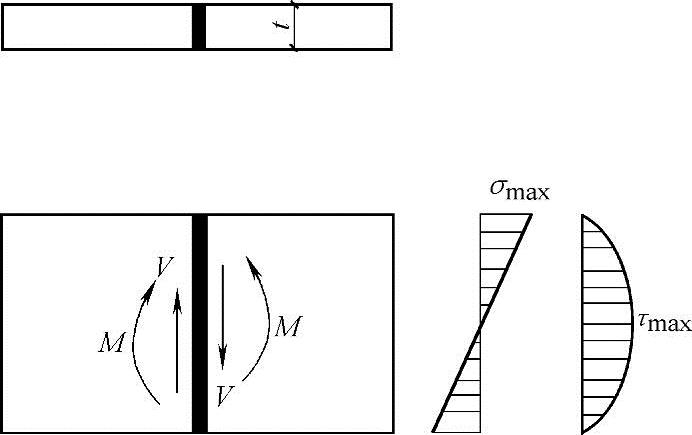
图3.4-1 矩形截面对接焊缝

2）工字形截面（图3.4-

2）。工字形截面对接焊缝在弯矩和剪力共同作用下，除按式（3.4-2）和式（3.4-3）验算最大正应力和最大剪应力外，对受有较大正应力σ₁和较大剪应力τ₁处（如翼缘与腹板连接处）还应按下式验算折算应力：

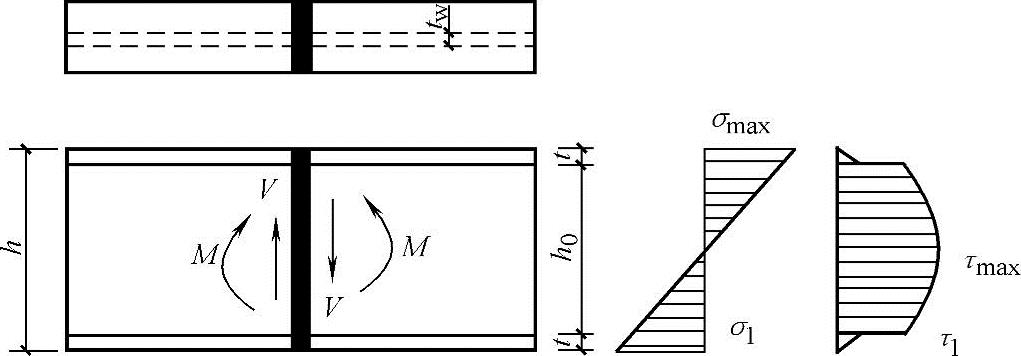
图3.4-2 工字形截面对接焊缝

式中 σ₁——腹板与翼缘连接处焊缝的正应力，；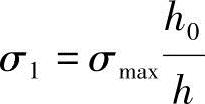

τ₁——腹板与翼缘连接处焊缝的剪应力，；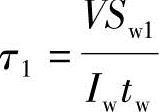

S_w1——焊缝截面计算剪应力处以上部分对中和轴的面积矩；

t_w——腹板厚度。

2.直角角焊缝强度计算

（1）角焊缝在轴心力作用下的计算

1）正面角焊缝（作用力垂直于焊缝长度方向）

式中 h_e——角焊缝的计算厚度，对直角角焊缝h_e=0.7h_f；

h_f——角焊缝的焊脚尺寸；

∑l_w——角焊缝计算长度之和；

β_f——正面角焊缝的强度设计值增大系数：对承受静力荷载和间接承受动力荷载的结构，β_f=1.22；对直接承受动力荷载的结构，β_f=1.0；

f^w_f——角焊缝的强度设计值，按表3.1-3选用。

2）侧面角焊缝（作用力平行于焊缝长度方向）

3）三面围焊（图3.4-3）

首先计算正面角焊缝所能承担的力N₃，其余内力N—N₃由侧焊缝承担：

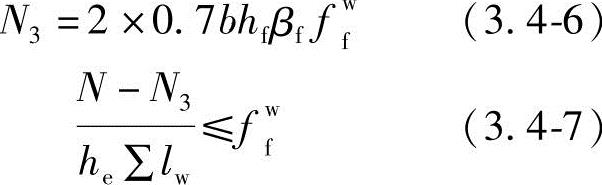
4）角钢用角焊缝连接，角钢与节点板采用两侧焊缝连接时（图3.4-4a），角钢肢背和肢尖焊缝分担的内力分别为

图3.4-3 三面围焊

N₁=k₁N （3.4-8）

N₂=k₂N （3.4-9）

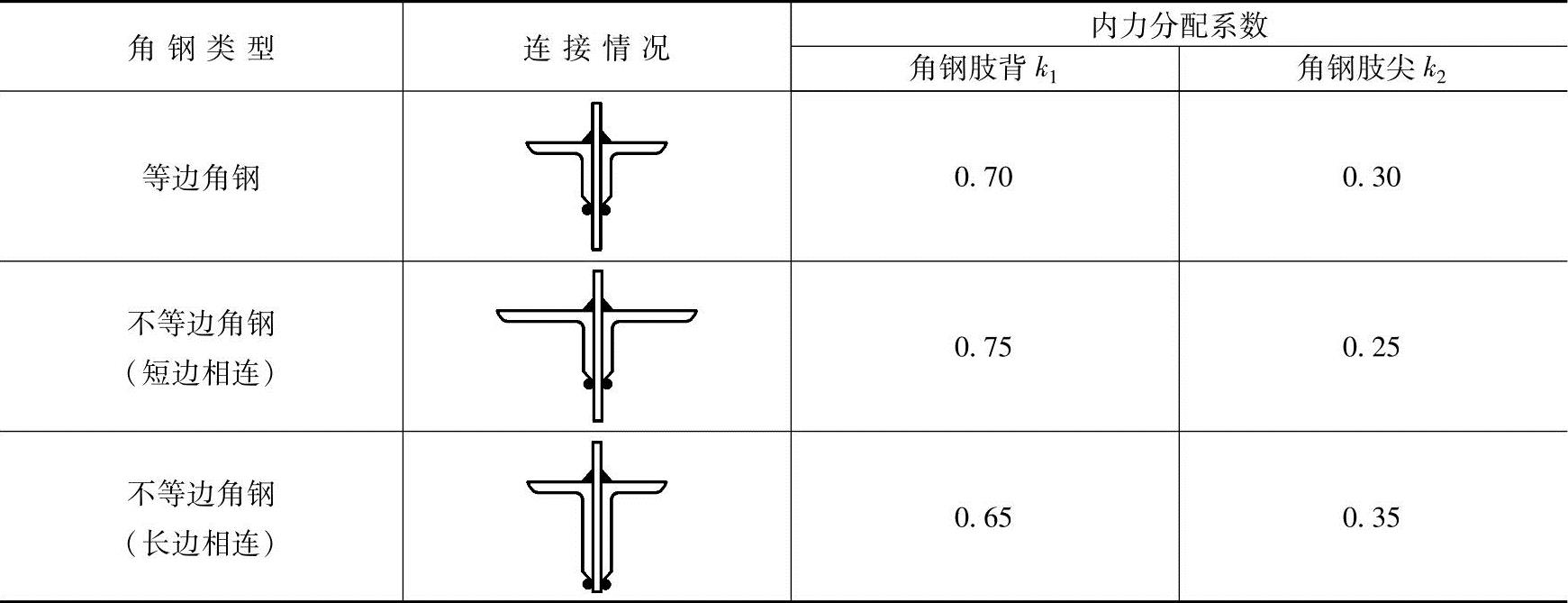
式中 k₁、k₂——角钢肢背和肢尖焊缝的内力分配系数，可按表3.4-2取用。

表3.4-2 角钢肢背和肢尖焊缝的内力分配系数

角钢与节点板采用三面围焊连接时（图3.4-4b），正面角焊缝和角钢肢背、肢尖焊缝承担的内力分别按下列公式计算：

角钢与节点板采用L形围焊连接时（图3.4-4c），正面角焊缝和角钢肢背焊缝分担的内力分别按下式计算：

N₃=2k₂N （3.4-13）

N₁=（1-2k₂）N （3.4-14）

图3.4-4 角钢与连接板的焊缝连接

按上述求出各条焊缝分担的内力后，假定角钢肢背和肢尖焊缝的焊脚尺寸分别为h_f1和h_f2，则可按下列公式对肢背和肢尖焊缝进行验算或分别计算出所需的焊缝计算长度：

（2）角焊缝在弯矩、剪力和轴心力共同作用时的受力计算角焊缝在各种力综合作用下的计算公式为

式中 σ_f——按焊缝有效截面计算，垂直于焊缝长度方向的正应力；

τ_f——按焊缝有效截面计算，沿焊缝长度方向的剪应力。

式（3.4-17）是焊缝计算的基本公式，在不同的受力状态下公式的形式可作相应的改变。

角焊缝在弯矩M、剪力V和轴心力N共同作用时（图3.4-5），可按下列公式进行计算：

1）矩形截面牛腿板与柱连接（图3.4-5a）

A点焊缝应满足下式要求：

式中 σ^M_f_A——弯矩M在焊缝A点产生的正应力，σ^M_fA=M/W^w_fA；

σ^N_f——水平力N在焊缝有效截面上产生的正应力，σ_f^N=N/A^w_f；

τ^V_f——剪力V在焊缝有效截面上产生的剪应力，τ^V_f=V/A^w_f；

W^w_fA——A点处角焊缝有效截面抵抗矩；

A^w_f——角焊缝有效截面面积。

2）工字形截面牛腿板与柱连接（图3.4-5b）

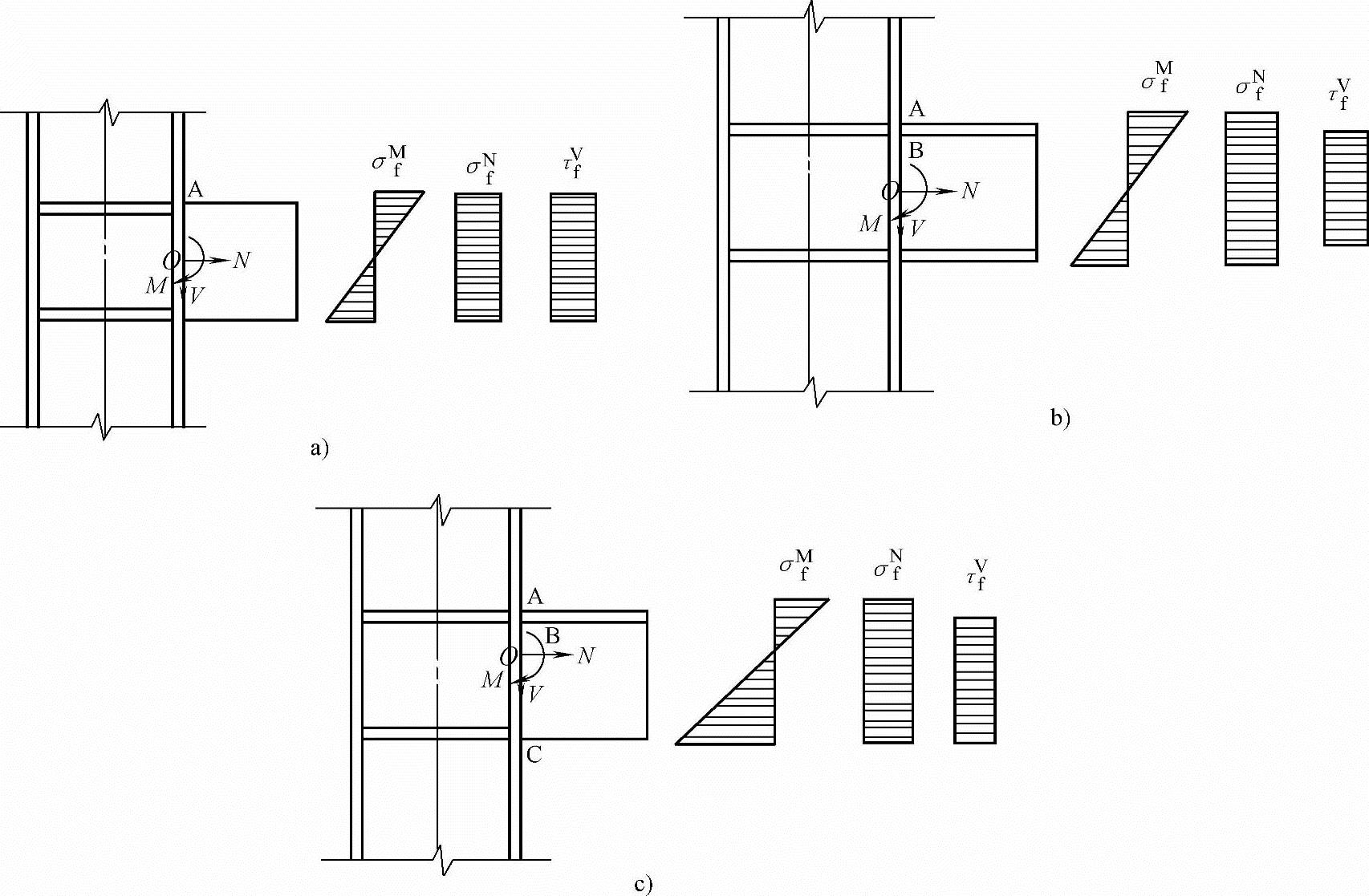
图3.4-5 弯矩、剪力、轴心力共同作用时的焊缝连接

a）矩形截面牛腿板与柱连接 b）工字形截面牛腿板与柱连接 c）T形截面牛腿板与柱连接

A点焊缝应满足下式要求：

σ^M_fA+σ^N_f≤β_f·f^w_f （3.4-19）

B点焊缝应满足下式要求：

C点焊缝应满足下式要求：

式中 σ^M_fA、σ^M_fB——弯矩M在焊缝A点和B点产生的正应力，σ^M_fA=M/W^w_fA，σ^M_fB=M/W^w_fB；

σ^N_f——水平力N在焊缝有效截面上产生的正应力，σ_f^N=N/A_f^w；

τ^V_f——剪力V在腹板焊缝有效截面上产生的剪应力，τ^V_f=V/A^w_f1；

W^w_fA、W^w_fB——A点和B点处角焊缝有效截面抵抗矩；

A^w_f——全部角焊缝有效截面面积之和；

A^w_f1——腹板焊缝有效截面面积。

3）T形截面牛腿板与柱连接（图3.4-5c）

A点、B点、C点焊缝分别按式（3.4-19）、式（3.4-20）和式（3.4-21）计算。

C点焊缝应满足下式要求：

式中 σ^M_f_C——弯矩M在焊缝C点产生的正应力，σ_f^MC=M/W^w_fC；

W^w_fC——C点处角焊缝有效截面模量。

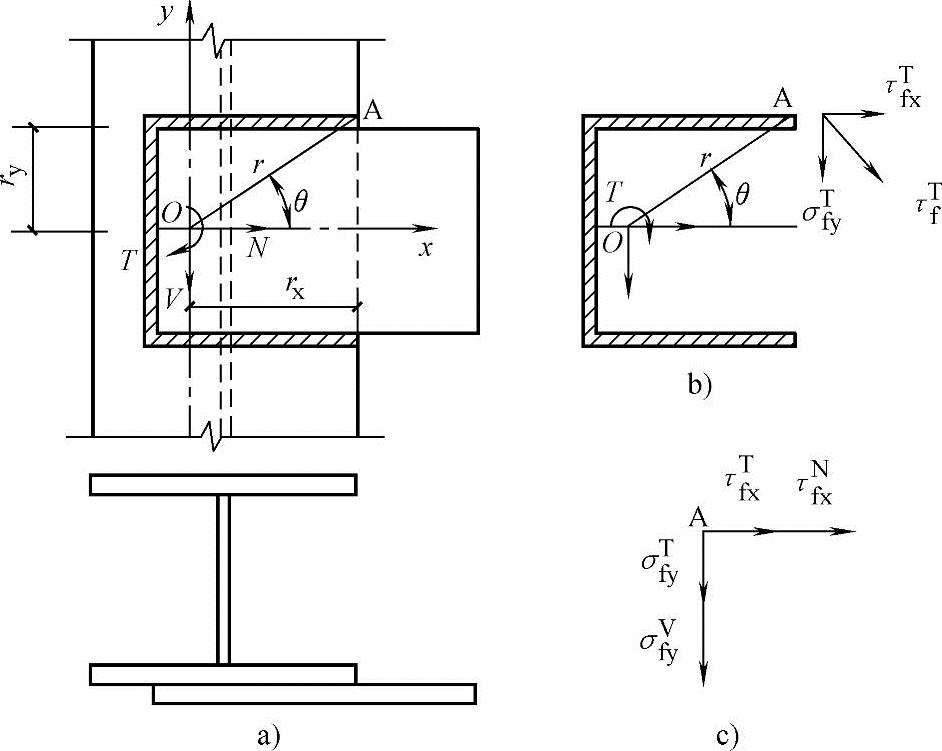
图3.4-6 扭矩、剪力、轴心力共同作用时的焊缝连接

（3）角焊缝在扭矩、剪力和轴心力共同作用时的受力计算（图3.4-6）在扭矩、剪力和轴心力共同作用下，A点角焊缝应满足下式要求：

式中 σ^T_fy——扭矩在A点产生的应力的竖向分量；

τ^T_fx——扭矩在A点产生的应力的水平分量；

r_x、r_y——r在x轴和y轴上的投影；

σ^V_fy——剪力产生的垂直于水平焊缝长度方向均匀分布的应力；

τ^N_fx——轴心力产生的平行于水平焊缝长度方向均匀分布的应力；

I₀——角焊缝有效截面的极惯性矩，I₀=I_x+I_y；

I_x、I_y——焊缝有效截面对x轴和y轴的惯性矩；

∑l_w——角焊缝有效长度（计算长度）之和。