首页理论教育3.3.3轴心受压构件整体稳定性分析与设计

3.3.3轴心受压构件整体稳定性分析与设计

2023-08-28 理论教育版权反馈

【摘要】：构件在轴心压力作用下发生整体失稳，可能有三种屈曲变形形式：弯曲屈曲、扭转屈曲和弯扭屈曲。表3.3-4 系数α1、α2、α3表3.3-5a 轴心受压构件截面分类（续）表3.3-5b 轴心受压构件截面分类4.构件长细比和换算长细比计算截面为双轴对称或极对称的构件截面为双轴对称或极对称的构件，其长细比可按式计算。

构件在轴心压力作用下发生整体失稳，可能有三种屈曲变形形式：弯曲屈曲、扭转屈曲和弯扭屈曲。

1.轴心受压构件的整体稳定计算

轴心受压构件的整体稳定按下式计算：

式中 N——构件的轴向压力设计值；

A——构件的毛截面面积；

φ——轴心受压构件的稳定系数，取截面两主轴稳定系数中的较小值。

2.整体稳定系数计算

整体稳定系数可根据构件的长细比、截面分类（表3.3-5）及构件钢号查表3.3-6确定或按式（3.3-7）计算。

（1）查表确定整体稳定系数φ 由式（3.3-4）确定构件的长细比λ，根据截面分类查表3.3-6确定长细比λ₁对应的稳定系数φ₁和长细比λ₂对应的稳定系数φ₂，这里λ₁≤λ≤λ₂。在表3.3-3的6个参数中，只有λ所对应的φ是待求的，根据线性插值（三点共线）即可按下列公式确定稳定系数φ。

表 3.3-3

由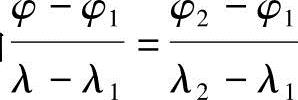，计算出φ：

（2）由公式计算整体稳定系数φ 整体稳定系数φ除查表确定外，还可按下列公式计算：

当λ_n≤0.215时：

φ=1-α₁λ_n² （3.3-7a）

当λ_n＞0.215时：

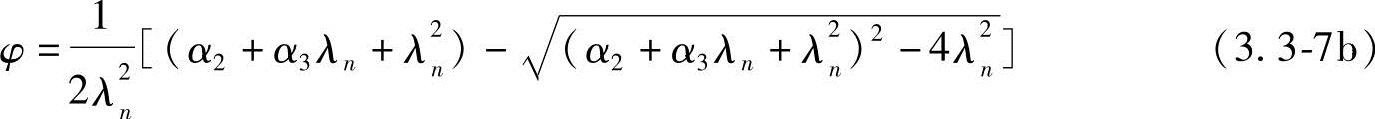
式中 λ_n——正则化长细比，；

λ——构件的长细比；

α₁、α₂、α₃——系数，可根据构件的截面分类和正则化长细比查表3.3-4确定。

3.轴心受压构件截面分类

轴心受压构件的截面分为a、b、c、d四类，分类情况见表3.3-5a和表3.3-5b。查表时应根据截面形式（轧制或焊接）、截面组成（实腹式或格构式）、板件加工方式（轧制、剪切、火焰切割）、板件厚度、对应的坐标轴等确定截面分类。

表3.3-4 系数α₁、α₂、α₃

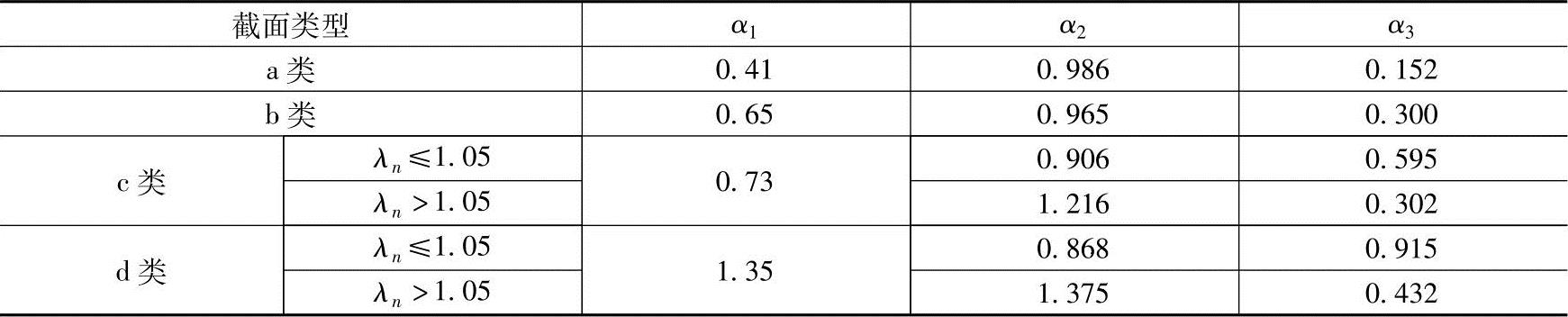
表3.3-5a 轴心受压构件截面分类（板厚t＜40mm）

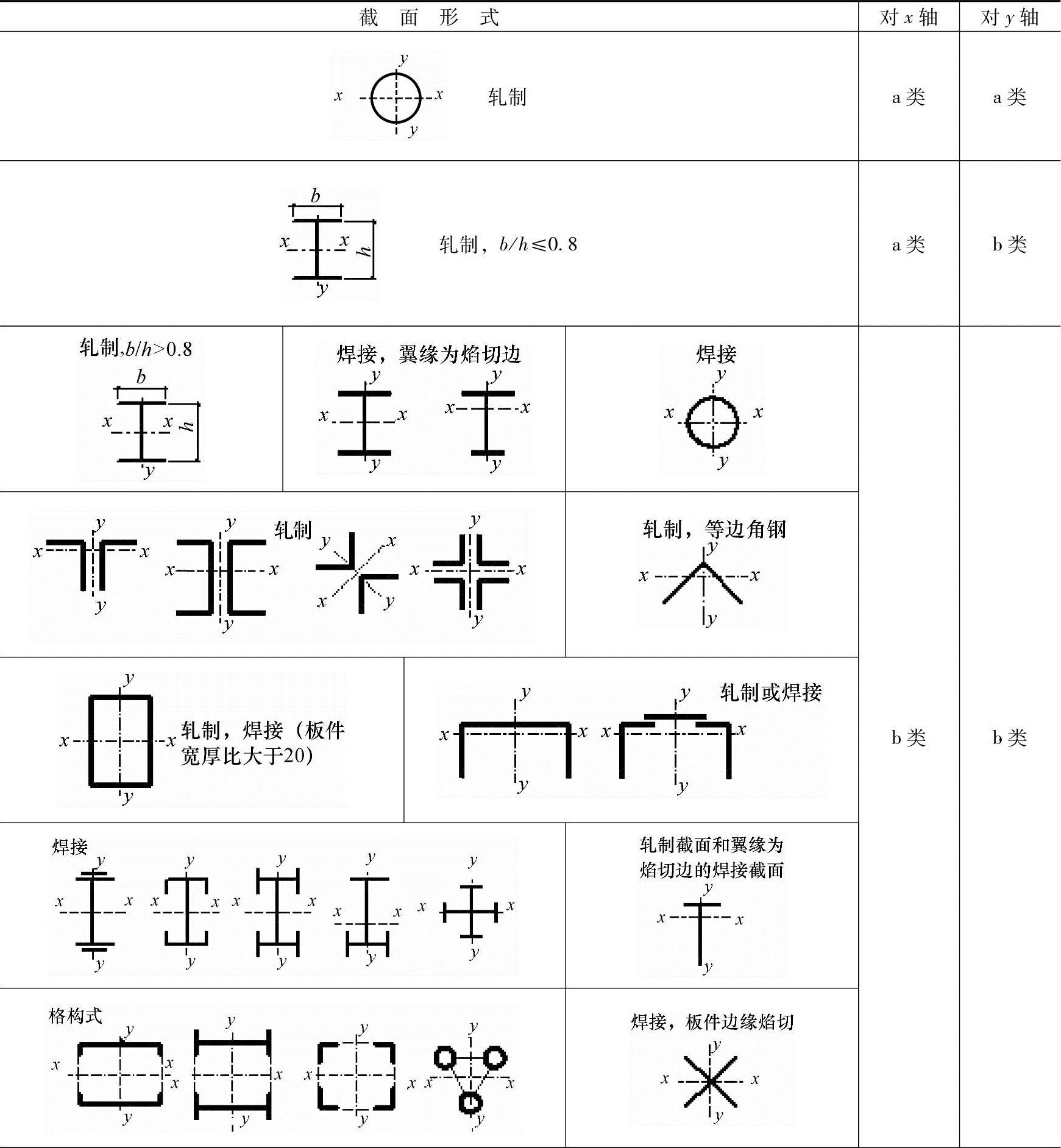
（续）

表3.3-5b 轴心受压构件截面分类（板厚t≥40mm）

4.构件长细比和换算长细比计算

（1）截面为双轴对称或极对称的构件截面为双轴对称或极对称的构件，其长细比可按式（3.3-4）计算。对双轴对称的十字形截面轴压构件，为了避免构件出现扭转屈曲，λ_x或λ_y取值不得小于5.07b/t，其中b/t为悬伸板件的宽厚比。

（2）截面为单轴对称的构件弯扭屈曲计算时，通过换算长细比将弯扭屈曲换算为弯曲屈曲，按式（3.3-5）进行计算。单轴对称截面构件绕非对称轴的屈曲仍为弯曲屈曲，长细比仍按式（3.3-4a）或式（3.3-4b）计算。

单轴对称截面构件对对称轴的换算长细比按下式计算：

式中 e₀——截面形心至剪心的距离；

i₀——截面对剪心的极回转半径；

λ_y——构件对对称轴的长细比；

λ_z——扭转屈曲的换算长细比；

I_t——毛截面抗扭惯性矩；

I_ω——毛截面扇性惯性矩。对T形截面（轧制、双板焊接、双角钢组合）、十字形截面、角形截面可近似取I_ω=0；

A——毛截面面积；

l_ω——扭转屈曲计算长度，对两端铰接端部截面可自由翘曲或两端嵌固端部截面的翘曲完全受到约束的构件，取l_ω=l_0y。

（3）单角钢截面和双角钢组合T形截面构件单角钢截面和双角钢组合T形截面构件绕对称轴的换算长细比可按下列简化方法计算：

1）等边单角钢截面（图3.3-1a）

当b/t≤0.54l_0y/b时：

当b/t＞0.54l_0y/b时：

式中 b、t——角钢的肢宽和肢厚。

2）等边双角钢截面（图3.3-1b）

当b/t≤0.58l_0y/b时：

当b/t＞0.58l_0y/b时：

3）长肢相并的不等边双角钢截面（图3.3-1c）

当b₂/t≤0.48l_0y/b₂时：

当b₂/t＞0.48l_0y/b₂时：

4）短肢相并的不等边双角钢截面（图3.3-1d）

当b₁/t≤0.56l_0y/b₁时：

λ_yz=λ_y（3.3-12a）

当b₁/t＞0.56l_0y/b₁时：

5）等边单角钢绕平行轴（图3.3-1e）

当b/t≤0.69l_0u/b时：

当b/t＞0.69l_0u/b时：

λ_uz=5.4b/t （3.3-13b）

式中 λ_u——构件绕u轴的长细比，λ_u=l_0u/i_u；

l_0u——构件对u轴的计算长度；

i_u——构件截面对u轴的回转半径。

等边单角钢绕平行轴按b类截面计算。

图3.3-1 单角钢截面和双角钢组合T形截面