计算考虑屈曲后强度的组合梁腹板

无局部压应力、承受静力荷载或间接承受动力荷载的组合梁可以考虑腹板屈曲后强度。承受动力荷载的梁，腹板的多次反复屈曲可能导致腹板边缘出现疲劳裂纹，缩短梁的疲劳寿命，因此，吊车梁等直接承受动力荷载的梁不宜考虑腹板屈曲后强度。

1.梁腹板屈曲后的抗剪承载力

单独承受剪力的梁腹板屈曲后，其抗剪承载力按下式计算：

当λ_s≤0.8时： V_u=h_wt_wf_v （3.2-32a）

当0.8＜λ_s≤1.2时： V_u=h_wt_wf_v[1-0.5（λ_s-0.8）] （3.2-32b）

当λ_s＞1.2时： V_u=h_wt_wf_v/λ_s^1.2 （3.2-32c）

式中 λ_s——用于腹板受剪计算的通用高厚比，按式（3.2-18d）和式（3.2-18e）计算。当组合梁仅设置支座处的支承加劲肋时，式（3.2-18e）中的h₀/a=0。

2.梁腹板屈曲后的抗弯承载力

单独承受弯矩的梁腹板屈曲后，其抗弯承载力按下式计算：

式中 α_e——梁截面抵抗矩的折减系数（有效截面抵抗矩和全部截面抵抗矩的比值）；

r_x——截面塑性发展系数；

I_x——梁按全截面有效确定的对x轴的惯性矩；

W_x——梁按全截面有效确定的截面抵抗矩；

h_c——梁按全截面有效确定的腹板受压区高度；

ρ——腹板受压区有效高度系数，根据通用高厚比λ_b的取值范围按下列公式计算：

当λ_b≤0.85时： ρ=1.0 （3.2-35a）

当0.85＜λ_b≤1.25时： ρ=1-0.82（λ_b-0.85） （3.2-35b）

当λ_b＞1.25时： ρ=（1-0.2/λ_b）/λ_b （3.2-35c）

式中 λ_b——用于腹板受弯计算的通用高厚比，按式（3.2-17d）和式（3.2-17e）计算。

3.考虑腹板屈曲后强度时梁的计算公式

为简化计算，一般采用下列无量纲化相关关系公式计算。

当M/M_f≤1.0时：

V≤V_u （3.2-36a）

当V/V_u≤0.5时：

M≤M_eu （3.2-36b）

其他情况时：

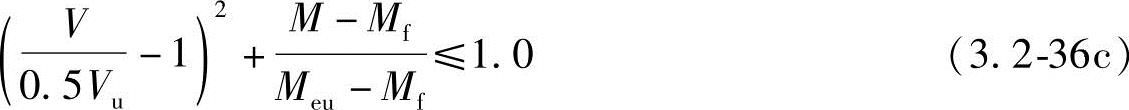
式中 M、V——梁所计算区格内同一截面处的弯矩和剪力设计值；计算时，当V＜0.5V_u时，取V=0.5V_u；当M＜M_f时，取M=M_f；

M_f——梁两翼缘所承担的弯矩设计值：

对双轴对称工字形截面： M_f=A_fh_ff

对单轴对称工字形截面：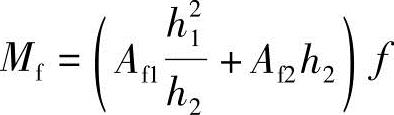

式中 A_f——双轴对称工字形截面一个翼缘的截面面积；

h_f——双轴对称工字形截面上、下翼缘形心间距离；

A_f1、h₁——对单轴对称工字形截面较大翼缘的截面面积及其形心至梁中和轴的距离；

A_f2、h₂——对单轴对称工字形截面较小翼缘的截面面积及其形心至梁中和轴的距离。

4.考虑腹板屈曲后强度时梁的加劲肋设计

考虑腹板屈曲后强度的梁一般不再考虑设置纵向加劲肋，而只在支座处或固定集中荷载作用位置处设置支承加劲肋。当仅配置支承加劲肋的梁，其抗弯和抗剪承载力不能满足式（3.2-36）的要求时，需增设中间横向加劲肋。

加劲肋应在腹板两侧成对配置，其外伸宽度和厚度除要满足式（3.2-24）的要求外，还应按下列方法进行受力计算。

（1）中间横向加劲肋计算 考虑腹板屈曲后强度时，中间横向加劲肋受到压力作用，可按轴心压力依据式（3.2-28）计算其在腹板平面外的整体稳定，轴心压杆的截面由肋板及其两侧各范围内的腹板组成。轴心压力按下列公式计算：

中间横向加劲肋：

N_s=V_u-h_wt_wτ_cr （3.2-37a）

中间横向加劲肋兼作承受固定集中荷载的支承加劲肋：

N_s=V_u-h_wt_wτ_cr+F （3.2-37b）

式中 V_u——腹板屈曲后的抗剪承载力，按式（3.2-32）计算；

h_w、t_w——腹板高度和厚度；

τ_cr——腹板临界剪应力，按式（3.2-18）计算；

F——加劲肋承受的固定集中荷载。

（2）支座支承加劲肋计算

1）支座支承加劲肋受力。当腹板在支座旁端区格考虑利用屈曲后强度时（即λ_s＞0.8时），支座支承加劲肋除承受支座反力外，还承受拉力场的水平分力作用，水平分力作用位置位于距腹板计算高度上边缘h₀/4处。拉力场的水平分力计算公式如下：

式中 h_w——腹板高度；

a——加劲肋间距。对设中间横向加劲肋的腹板为支座端区格的加劲肋间距；对不设

中间横向加劲肋的腹板为梁支座至跨内剪力为零点的距离。

中间横向加劲肋间距较大（a＞2.5h₀）和不设中间横向加劲肋的腹板，当腹板局部稳定满足时（满足式（3.2-13）），可取H=0。

2）支座支承加劲肋计算。为了增加抗弯能力，需要将梁端部延长，并设置封头板（图3.2-7）。设置封头板后，梁支座支承加劲肋可按下列方法之一进行计算：

①将封头板与支座支承加劲肋之间视为竖向压弯构件，构件计算长度取腹板高度，计算其强度和腹板平面外的整体稳定；

②将支座支承加劲肋1作为承受支座反力R的轴心受压构件计算，封头板的截面面积则不应小于按下式计算的数值：

图3.2-7 设置封头肋板的梁端构造

1—支承加劲肋 2—封头肋板

式中 e——支座加劲肋至封头板的距离；

f——钢材强度设计值。

表3.2-1 截面塑性发展系数γ_x、γ_y

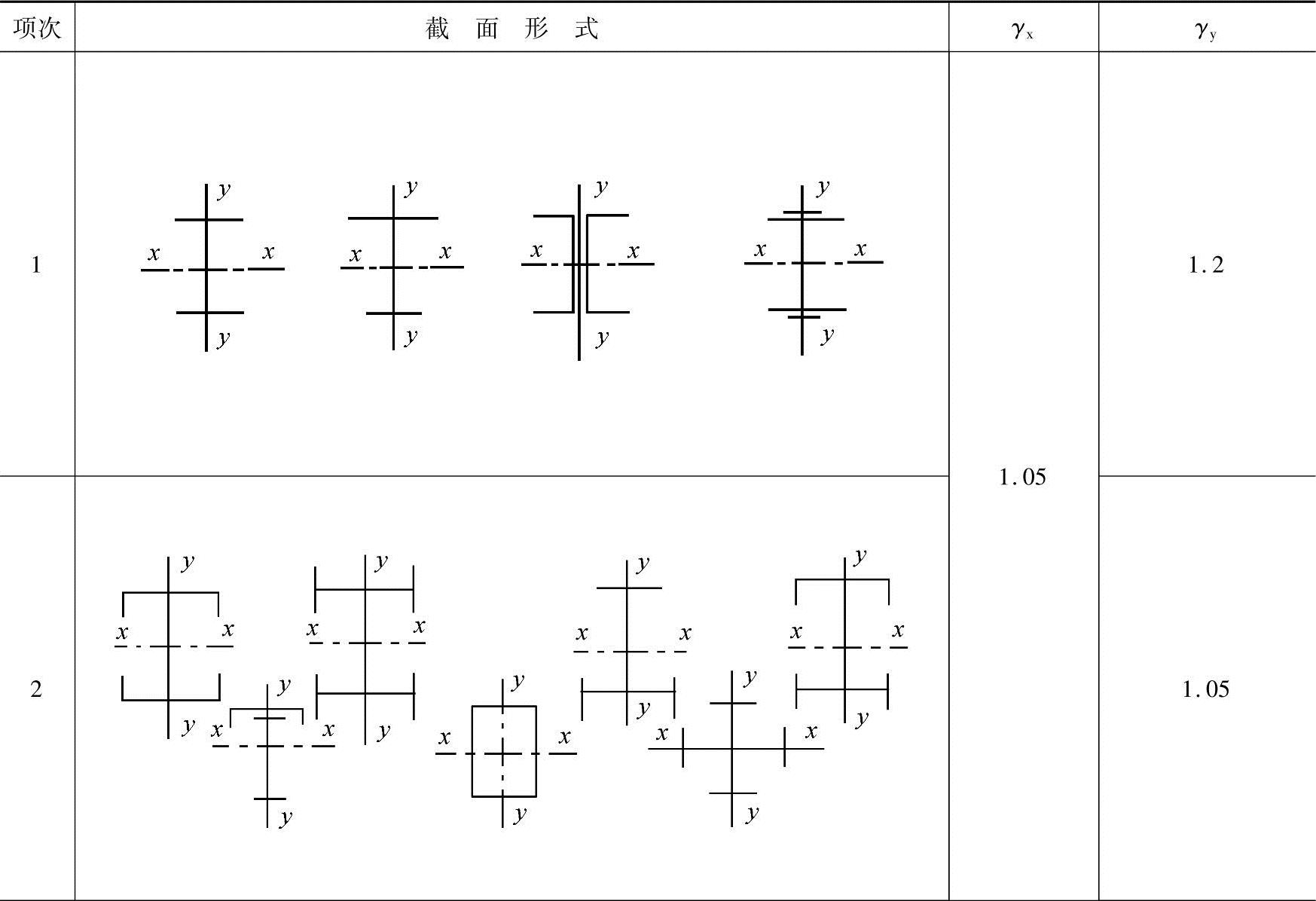
（续）

注：当压弯构件受压翼缘的自由外伸宽度与其厚度之比大于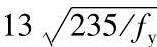而不超过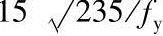时，应取γ_x=1.0。

表3.2-2 H型钢或等截面工字形简支梁不需计算整体稳定性的最大l₁/b₁

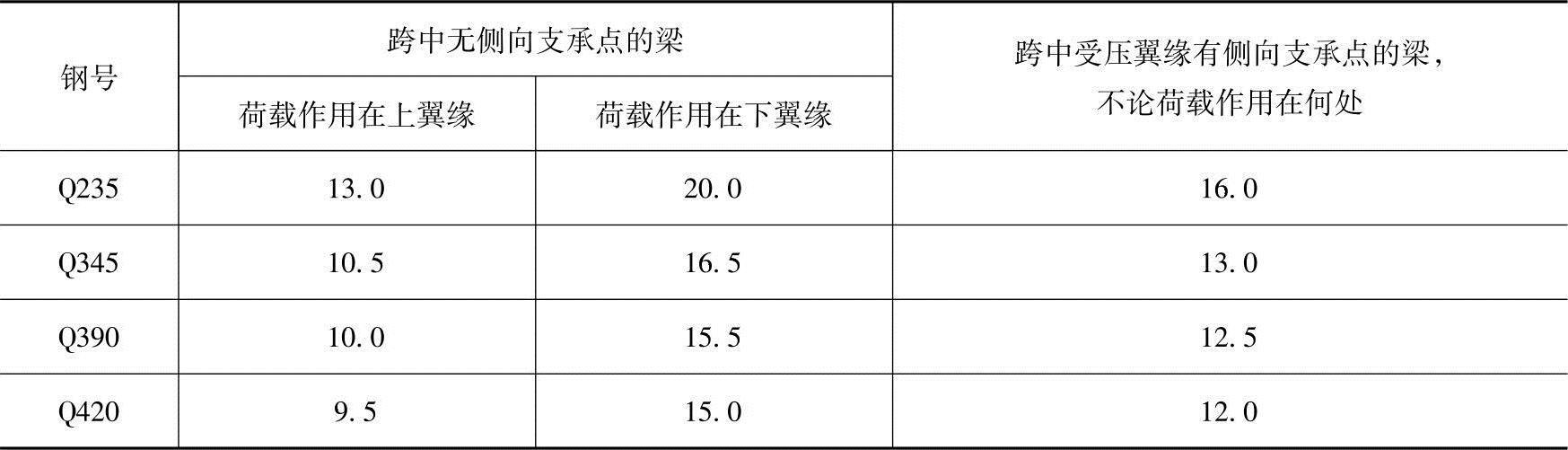
注：其他钢号的梁不需计算整体稳定性的最大l₁/b₁值，应取Q235钢的数值乘以。

表3.2-3 H型钢和等截面工字形简支梁的等效弯矩系数β_b

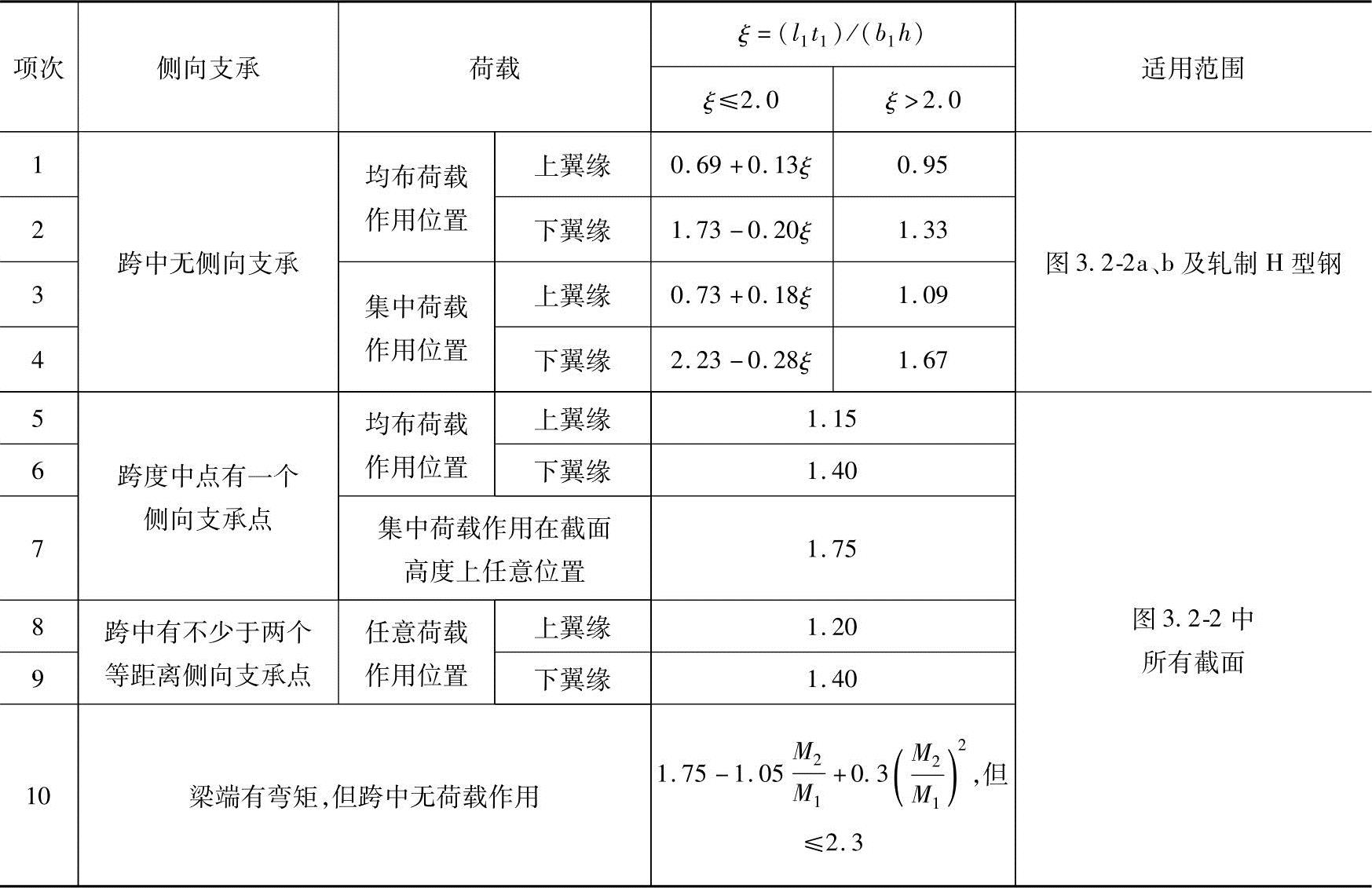
注：1.ξ=（l₁t₁）/（b₁h）为参数，其中l₁和b₁为简支梁受压翼缘的自由长度和宽度。

2.M₁和M₂为梁端弯矩，使梁产生同向曲率时取同号，产生反向曲率时取异号，|M₁|≥|M₂|。

3.表中项次3、4和7的集中荷载是指一个或少数几个集中荷载位于跨中央附近的情况，对于其他情况的集中荷载，应按表中项次1、2、5、6内的数值采用。

4.表中项次8、9的β_b，当集中荷载作用在侧向支承点处时，取β_b=1.20。

5.荷载作用在上翼缘系指荷载作用点在翼缘表面，方向指向截面形心；荷载作用在下翼缘系指荷载作用点在翼缘表面，方向背向截面形心。

6.对α_b＞0.8的加强受压翼缘工字形截面，下列情况的β_b值应乘以相应的系数：

项次1：当ξ≤1.0时，β_b值应乘以0.95；

项次3：当ξ≤0.5时，β_b值应乘以0.90；

当0.5＜ξ≤1.0时，β_b值应乘以0.95。

表3.2-4 轧制普通工字钢简支梁的稳定系数φ_b

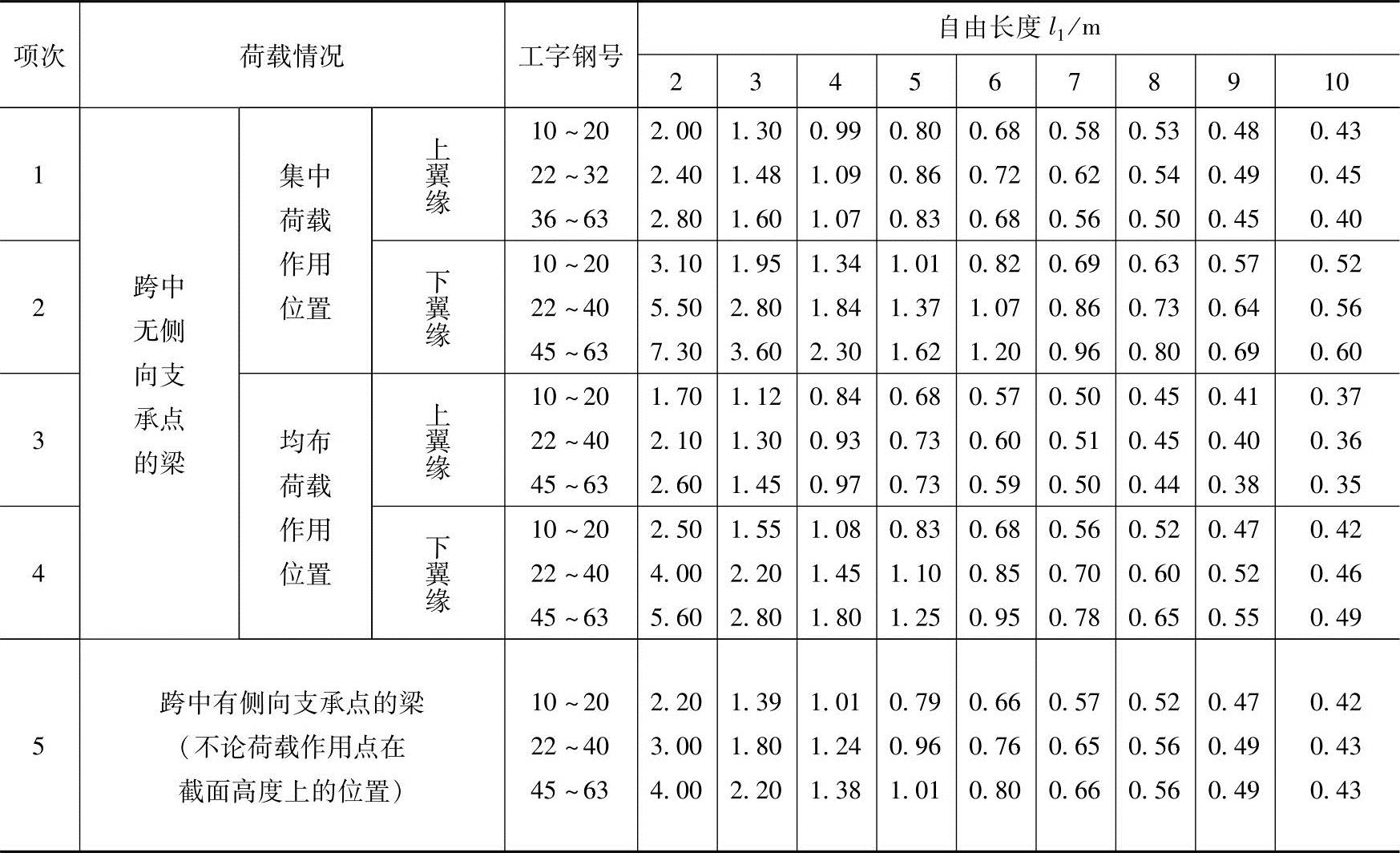
注：1.同表3.2-3中的注3和注5。

2.表中φ_b适用于Q235钢。对其他钢号，表中数值应乘以235/f_y。

表3.2-5 双轴对称工字形等截面（含H型钢）悬臂梁的等效弯矩系数β_b

注：l₁为受压翼缘的自由长度；b、t分别为受压翼缘的宽度和厚度；h为梁截面高度。

表3.2-6 简支梁挠度计算公式

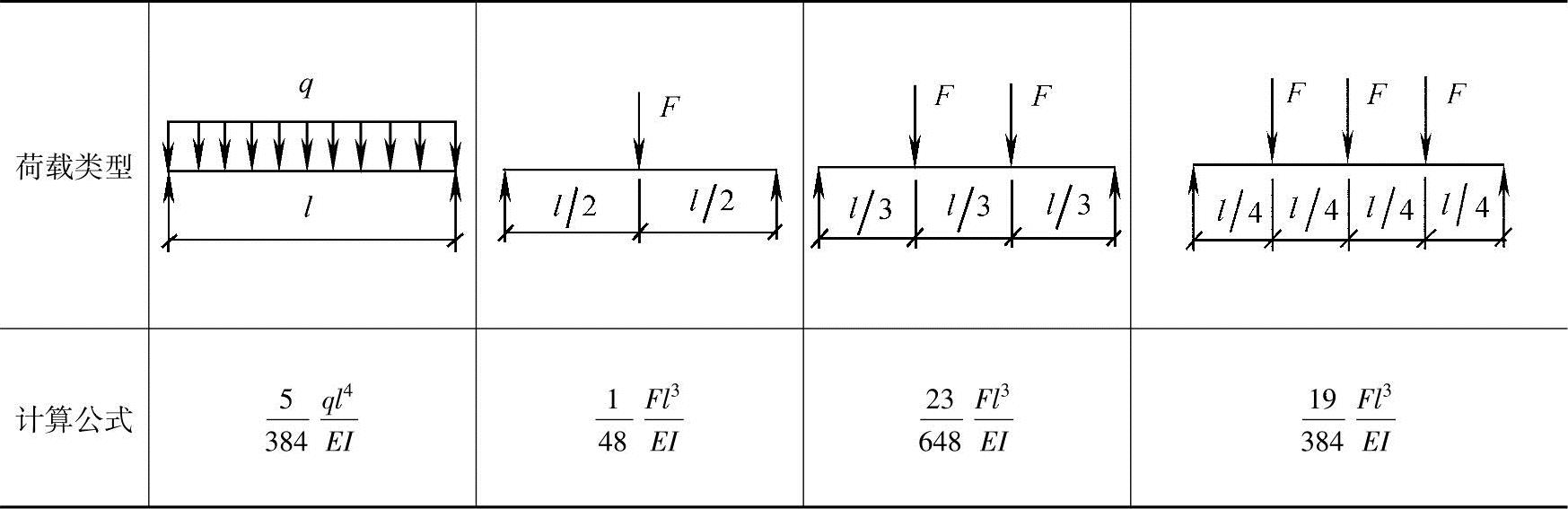
表3.2-7 受弯构件挠度容许值（吊车梁、楼盖梁、屋盖梁、工作平台梁和墙架构件）

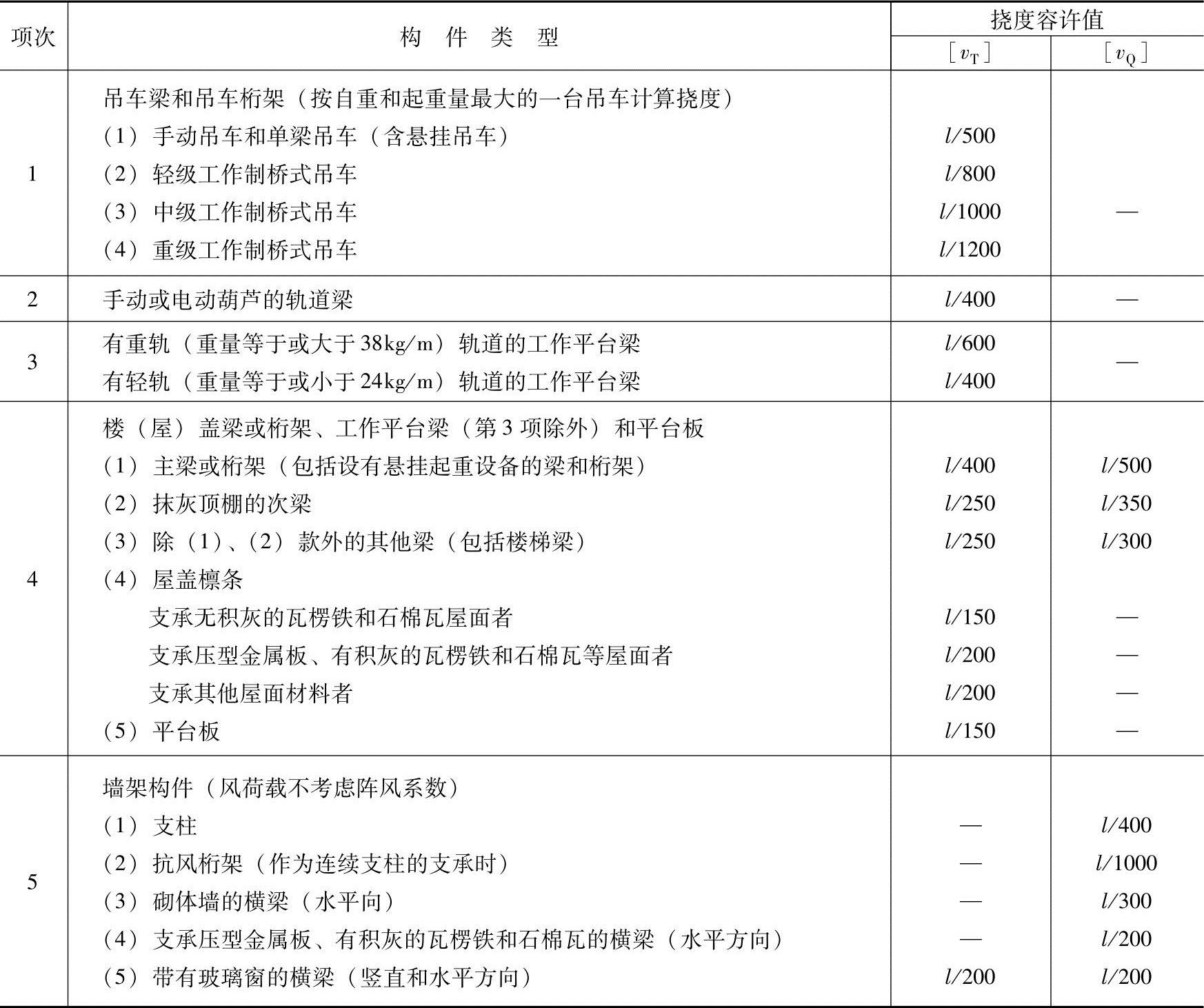
注：1.l为受弯构件的跨度（对悬臂梁和伸臂梁为悬伸长度的2倍）。

2.[v_T]为永久和可变荷载标准值产生的挠度（如有起拱应减去拱度）的容许值；[v_Q]为可变荷载标准值产生的挠度的容许值。

表3.2-8 吊车梁或吊车桁架制动结构挠度容许值

注：l为制动结构的跨度。

【例3.2-1】 某一在主平面内受弯的实腹构件，当构件截面上有螺栓（或铆钉）孔时，试问，下列何项计算要考虑螺栓（或铆钉）孔引起的截面削弱？

（A）构件变形计算

（B）构件整体稳定性计算

（C）构件抗弯强度计算

（D）构件抗剪强度计算

答案：（C）

解答：在受弯构件计算中，抗弯强度计算用净截面抵抗矩，其他计算采用毛截面参数。

【例3.2-2】 图3.2-8所示为一焊接组合截面吊车梁，钢梁截面尺寸如图所示。吊车为重级工作制（A7），吊车轨道型号为QU100，轨道高度为150mm。吊车最大轮压F=355kN，吊车竖向荷载动力系数为1.1，可变荷载分项系数为1.4，图示车轮作用处最大弯矩设计值为M=4932kN·m，对应的剪力设计值为316kN。吊车梁材料采用Q345B钢，I_nx=2.433×10¹⁰mm⁴。

问题1：车轮作用处钢梁的局部压应力（N/mm²）与下列何项数值最接近？

图3.2-8 吊车梁

（A）105 （B）111 （C）115 （D）120

问题2：车轮作用处钢梁的折算应力（N/mm²）与下列何项数值最接近？

（A）149.6 （B）152.3 （C）160.5 （D）172.3

问题1答案：（B）

问题2答案：（B）

解答：

最大轮压下腹板局部承压强度验算：

吊车最大轮压设计值：F_d=1.4×1.1×355kN=546.7kN

重级工作制吊车：ψ=1.35

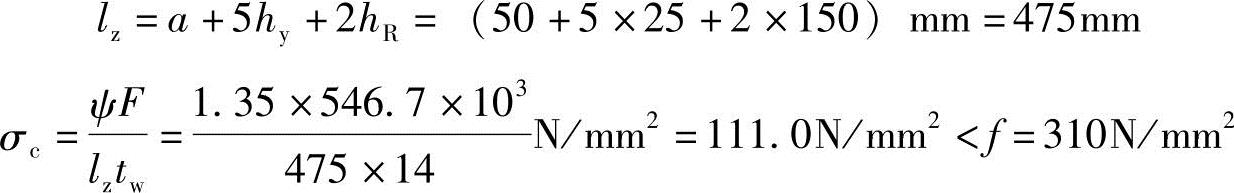
计算点正应力计算：

计算点剪应力计算：

上翼缘对中和轴的面积矩：S₁=500×25×（850+12.5）mm³=1.078×10⁷mm3

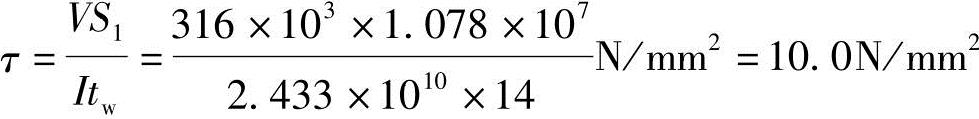
折算应力：

σ_c与σ同号，β₁=1.1

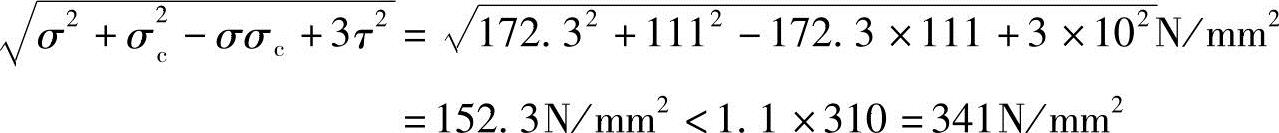
【例3.2-3】 某工作平台的次梁间距为3m，次梁跨度为4.5m，跨中无侧向支承，两端与主梁铰接。平台上可变荷载标准值为6kN/m²，永久荷载标准值（不包括次梁自重）为2.72kN/m²。次梁截面为HN346×174×6×9，I_x=10456cm⁴，W_x=649cm³，i_y=3.86cm，A=53.19cm²，自重41.8kg/m（0.41kN/m），钢材为Q235B钢。假设平台板与次梁上翼缘无可靠连接，则在整体稳定计算时，最大压应力（N/mm²）与下列何项数值最为接近？

（A）166.6 （B）176.4 （C）187.3 （D）190.5

答案：（C）

解答：荷载分项系数永久荷载取1.2，可变荷载取1.4。

跨中最大弯矩设计值：

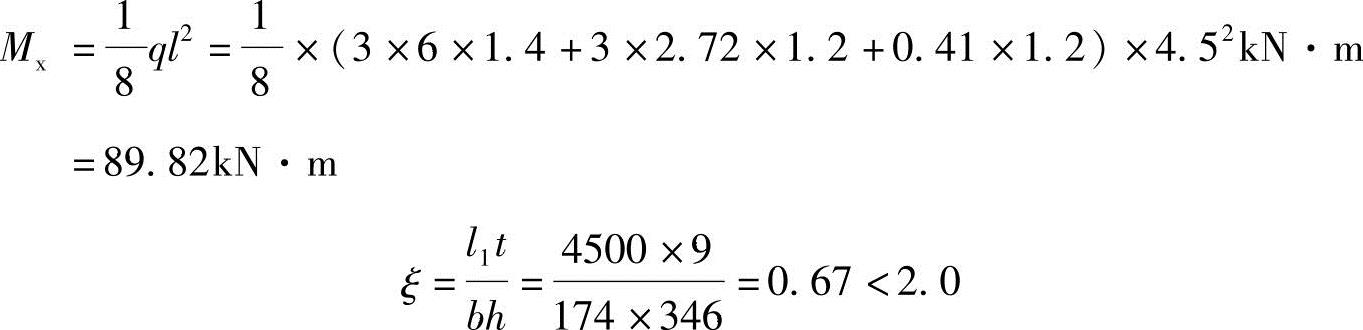
按表3.2-3项次1计算β_b：

按式（3.2-8）计算稳定系数：

由式（3.2-9）计算：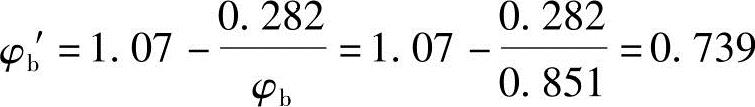

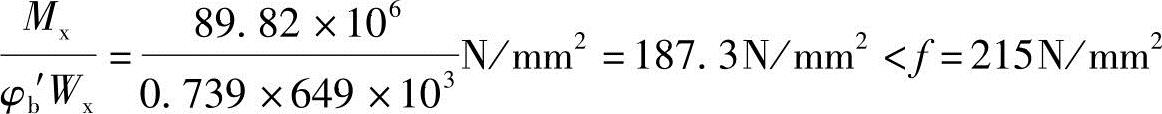
【例3.2-4】 某工作平台的次梁的已知条件与【例3.2-3】相同。要求对次梁作挠度验算。试问，其最大挠度与跨度的比值，与下列何项数值最为接近？

（A）1/600 （B）1/623 （C）1/663 （D）1/683

答案：（D）

解答：

次梁上作用的荷载标准值：q=（3×6+3×2.72+0.41）kN/m=26.57kN/m

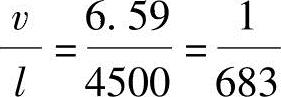
【例3.2-5】 如图3.2-9所示某屋面坡度为1/2.5（α=21.8°），屋面檩条跨度为6m，跨中设一根拉条，檩条采用[10轻型槽钢，I_x=173.89cm⁴，I_y=20.39cm⁴，形心距腹板边缘距离为14.4mm，距翼缘边缘距离为31.6mm。檩条上分布荷载设计值p=1.2kN/m。不考虑拉条连接处孔洞的削弱，则檩条截面上a点和b点处的应力（N/mm²）与下列何组数值最为接近？（负值表示压应力，正值表示拉应力）

图3.2-9 屋架檩条

（A）-72.6，171.0 （B）-64.7，-137.3

（C）64.7，-137.3 （D）-72.6，-171.0

答案：（D）

解答：

檩条线荷载沿屋架上弦方向分量：

p_x=psinα=1.2×0.371kN/m=0.445kN/m

檩条线荷载垂直于屋架上弦方向分量：

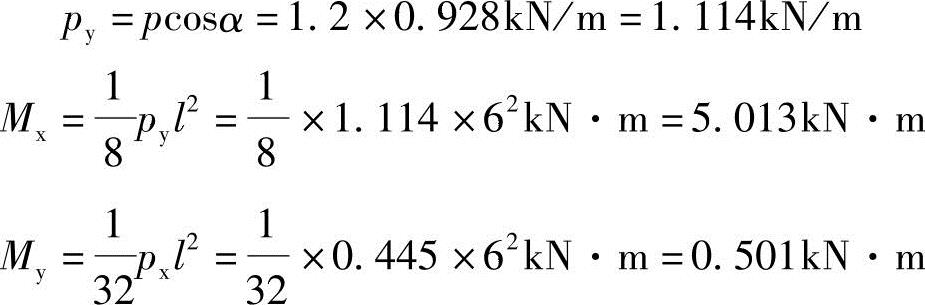
查表3.2-1：γ_ya=1.2，γ_yb=1.05，γ_x=1.05

W_nx=I_x/y₁=173.89×10⁴/50mm³=3.478×10⁴mm³

W_nya=I_y/x_a=20.39×10⁴/31.6mm³=6.453×10³mm³

W_nyb=I_y/x_b=20.39×10⁴/14.4mm³=1.416×10⁴mm³

M_x在a、b两点产生压应力，M_y在a点产生拉应力、在b点产生压应力。

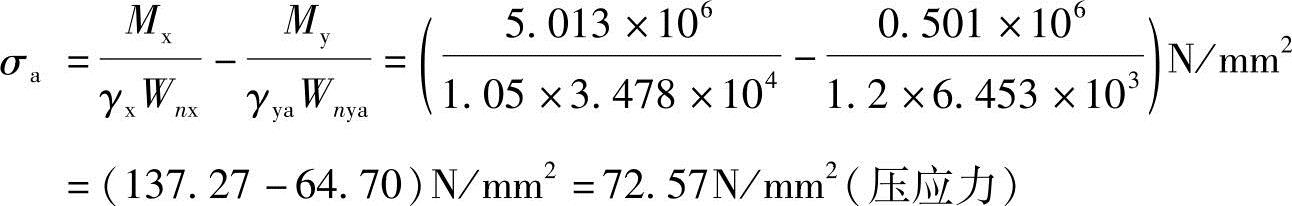
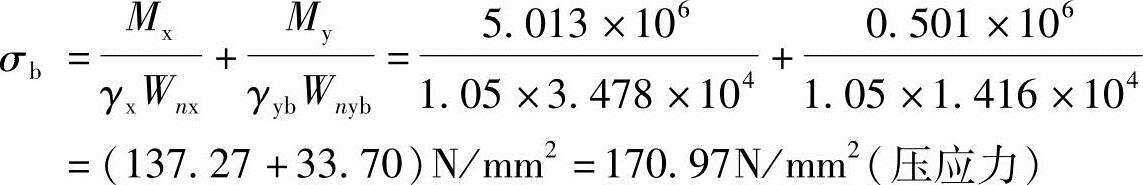
【例3.2-6】 如图3.2-10所示某平台主梁跨度15m，每隔3m有次梁从两侧与其连接，次梁传递给主梁的集中荷载设计值F=151kN，主梁自重（包括加劲肋重量）标准值q_k=1.5kN/m，主梁截面及加劲肋布置如图3.2-10所示，材料为Q235B。关于各区格的局部稳定下列哪项叙述是正确的？

（A）区格Ⅱ、Ⅲ、Ⅳ、Ⅴ均满足局部稳定要求

（B）区格Ⅱ、Ⅲ满足局部稳定要求，区格Ⅳ、Ⅴ不满足局部稳定要求

（C）区格Ⅱ、Ⅲ、Ⅳ满足局部稳定要求，区格Ⅴ不满足局部稳定要求

（D）区格Ⅱ、Ⅲ、Ⅳ、Ⅴ均不满足局部稳定要求

答案：（A）

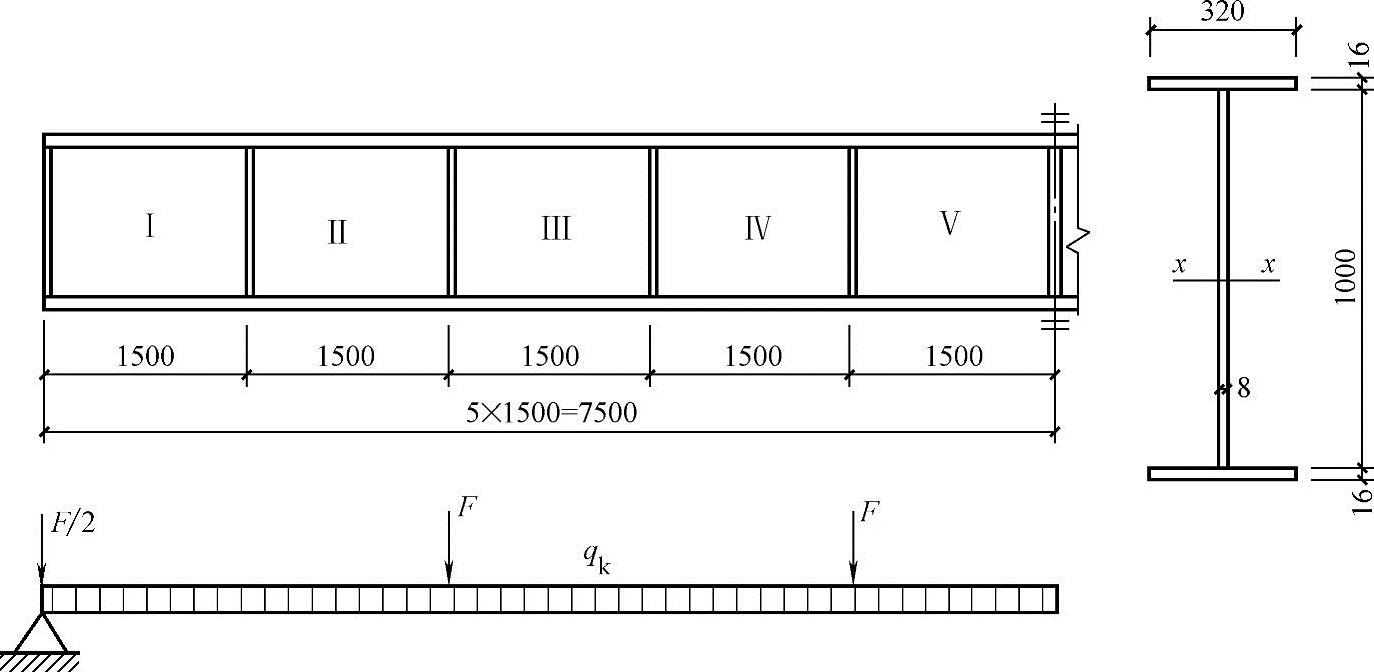
图3.2-10 平台主梁加劲肋布置

解答：主梁截面参数：A=18240mm²，I_x=3.3095×10⁹mm⁴，I_y=9.7424×10⁷mm4

支座处支反力：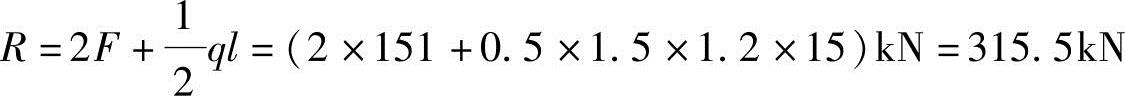

各区格平均弯矩（图3.2-11a）按区格中央部位弯矩计算：

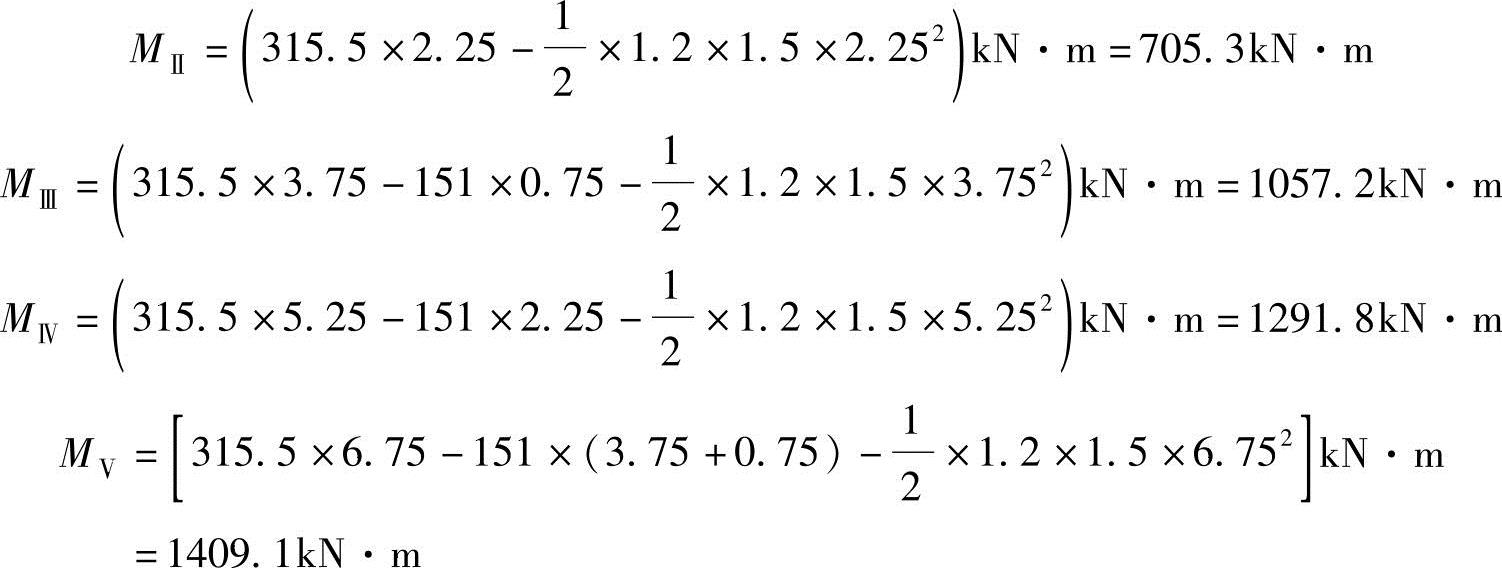
各区格平均弯矩产生的腹板计算高度边缘的弯曲压应力：

各区格平均剪力（图3.2-11b）按区格中央部位剪力计算：

V_Ⅱ=（315.5-1.2×1.5×2.25）kN=311.5kN

V_Ⅲ=（315.5-151-1.2×1.5×3.75）kN=157.8kN

V_Ⅳ=（315.5-151-1.2×1.5×5.25）kN=155.1kN

V_Ⅴ=（315.5-2×151-1.2×1.5×6.75）kN=1.35kN

图3.2-11 各区格中央部位的弯矩和剪力

a）弯矩（kN·m） b）剪力（kN）

各区格平均剪力产生的平均剪应力：

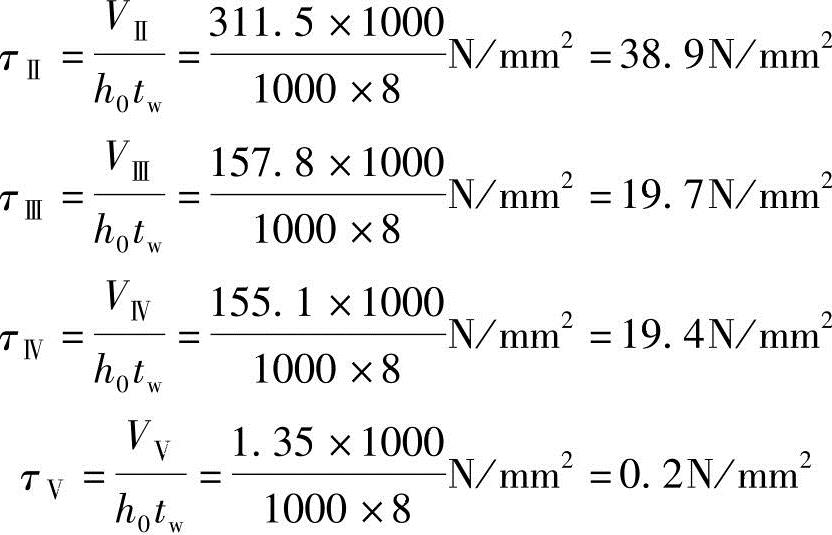
各区格临界应力计算：

临界弯曲压应力：主梁侧面连接有次梁，可约束主梁的受压翼缘扭转，通用高厚比λ_b

按式（3.2-17d）计算：

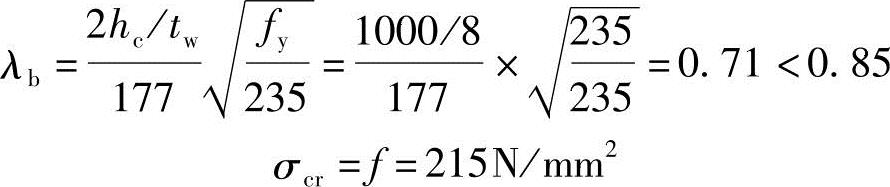
临界剪应力：

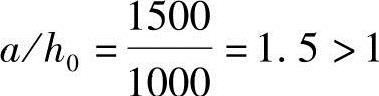，通用高厚比λ_s按式（3.2-18e）计算：

临界剪应力τ_cr按式（3.2-18b）计算：

τ_cr=[1-0.59（λ_s-0.8）]f_v=[1-0.59（1.14-0.8）]×125N/mm²=99.9N/mm²

各区格局部稳定计算：

只有横向加劲肋，按式（3.2-13）计算局部稳定，各区格内无集中荷载，σ_c=0。

区格Ⅱ： 满足

区格Ⅲ： 满足

区格Ⅳ： 满足

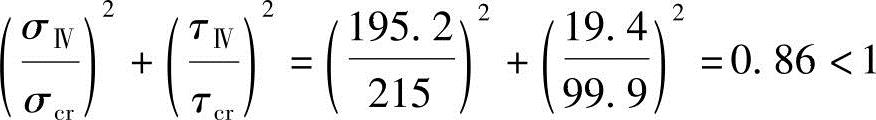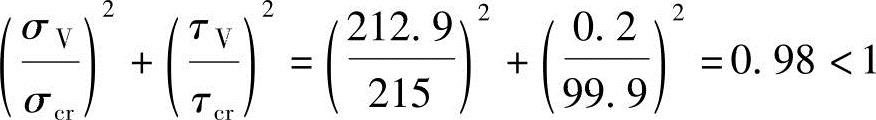区格Ⅴ： 满足

【例3.2-7】 如图3.2-12所示某平台主梁跨度15m，每隔3m有次梁从两侧与其连接，次梁传递给主梁的集中荷载设计值F=151kN，主梁自重（包括加劲肋重量）标准值q_k=1.4kN/m，主梁截面及加劲肋布置如图3.2-12所示，截面面积A=16240mm²，惯性矩I_x=3.1428×10⁹mm⁴，I_y=8.740×10⁷mm⁴，材料为Q235B。用考虑腹板屈曲后强度的方法校核腹板强度，下列哪项叙述是正确的？

（A）区格Ⅰ左侧、区格Ⅰ右侧、区格Ⅱ右侧腹板强度满足，区格Ⅲ中央腹板强度不满足

（B）区格Ⅰ右侧、区格Ⅰ左侧腹板强度满足，区格Ⅱ右侧、区格Ⅲ中央腹板强度不满足

（C）区格Ⅰ左侧、区格Ⅱ右侧、区格Ⅲ中央腹板强度满足，区格Ⅰ右侧腹板强度不满足

（D）区格Ⅰ左侧、区格Ⅰ右侧、区格Ⅱ右侧、区格Ⅲ中央腹板强度均满足

答案：（B）

图3.2-12 平台主梁加劲肋布置

解答：

梁受压翼缘扭转受到约束，则

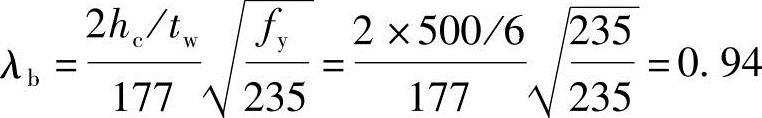
根据式（3.2-35）：

0.85＜λ_b＜1.25，ρ=1-0.82（λ_b-0.85）=1-0.82×（0.94-0.85）=0.93

由式（3.2-34）：

由式（3.2-33）：

M_eu=r_xα_eW_xf=1.05×0.992×3.1428×10⁹/516×215N·mm=1364.0kN·m

当a/h₀=3＞1.0：

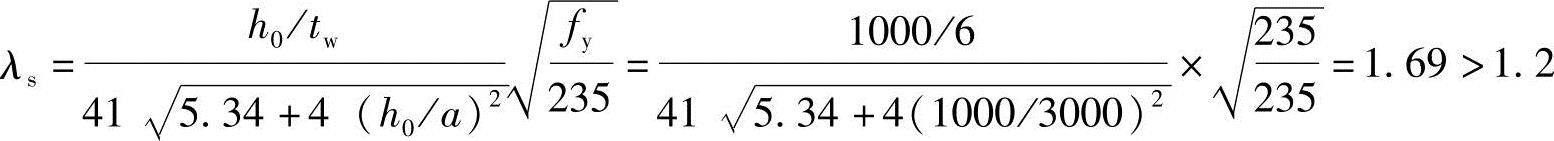
根据式（3.2-32c）：

V_u=h_wt_wf_v/λ_s^1.2=1000×6×125/1.69^1.2N=399.6kN

加劲肋及跨中位置处的弯矩及剪力值如图3.2-13所示。

M_f=A_fh_ff=320×16×1016×215N·mm=1118.4kN·m

区格Ⅰ左侧：

V=314.6kN，M=0

M=0＜M_f=1118.4kN·m，按式（3.2-36a）：

V=314.6kN＜V_u=399.6kN 满足

区格Ⅰ右侧：

V=310.8kN，M=936.2kN·m

M=936.2kN·m＜M_f=1118.4kN·m，按式（3.2-36a）：

V=310.8kN＜V_u=399.6kN 满足

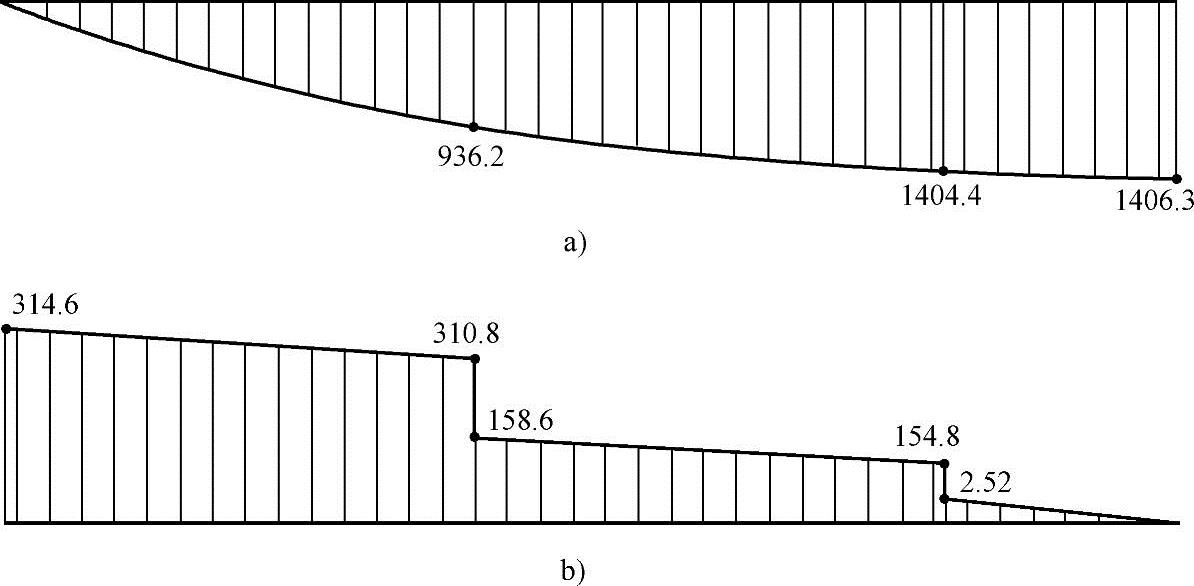
图3.2-13 肋板处及跨中的弯矩和剪力

a）弯矩（kN·m） b）剪力（kN）

区格Ⅱ右侧：

V=154.8kN，M=1404.4kN·m

V=154.8kN＜0.5V_u=0.5×399.6kN=199.8kN，按式（3.2-36b）：

M=1404.4kN·m＞M_eu=1364.0kN·m 不满足

区格Ⅲ中央：

V=0kN，M=1406.3kN·m

V=0kN＜0.5V_u=0.5×399.6kN=199.8kN，按式（3.2-36b）：

M=1406.3kN·m＞M_eu=1364.0kN·m 不满足