试进行结构布置，并对板、次梁和主梁进行设计。长边与短边方向的跨度比为3，故按单向板设计。图2-29 梁板结构平面布置板的荷载组合设计值：p=γGgk+γQqk=kN/m2=11.4kN/m2板的计算简图次梁截面为200mm×500mm，现浇板在墙上支承长度取120mm。......
2023-08-30
2.16.2双向板肋梁楼盖设计实例
【摘要】：图2.16-4 双向板活荷载最不利布置图在反对称荷载±q/2作用下，所有中间支座可视为简支边。沿墙边及墙角的板顶构造钢筋与单向板肋梁楼盖中相同。图2.16-6 支承双向板梁的荷载图2.16-7 等效荷载 某钢筋混凝土现浇肋形楼盖的次梁，跨中承受最大正弯矩设计值M=115kN·m。
1.按弹性理论的计算方法
（1）单跨双向板按弹性理论的实用计算法 根据弹性理论，把双向板视为各向同性体，当板厚h远比平面尺寸小，挠度不超过0.2h时，双向板可按弹性薄板小挠度理论计算。为了便于工程设计，《建筑结构静力计算手册》根据弹性薄板理论公式编制了各种支承情况板的内力和位移系数的表格，根据上述不同的计算简图，即可算得有关弯矩。
（2）多跨连续双向板按弹性理论的实用计算法 对同一方向相邻最小跨度与最大跨度之比大于0.75的多跨连续双向板均可按下述方法计算板中内力
1）跨中最大弯矩：当求某区格跨中最大弯矩时，其活荷载的最不利布置，如图2.16-4a所示，通常称为棋盘形荷载布置。为了能利用单跨双向板的内力计算表格，将棋盘形布置的活荷载分解为图2.16-4b、c所示的对称与反对称荷载情况，每种情况的荷载为：
对称情况 
反对称情况 
在对称荷载作用下的多跨板，所有中间区格板均可认为是四边固定边；边区格板除边支承情况按实际确定外，其他三边亦均可视为固定边；而四个角区格板则两个边支承情况按实际确定，两个内边按固定考虑。经过这样处理，四边支承双向板的所有区格只有六种可能的边界条件，这样利用前述单跨双向板的内力计算表格，可计算出每一区格在g+q/2作用下当泊松比μ=0时的跨中最大弯矩。
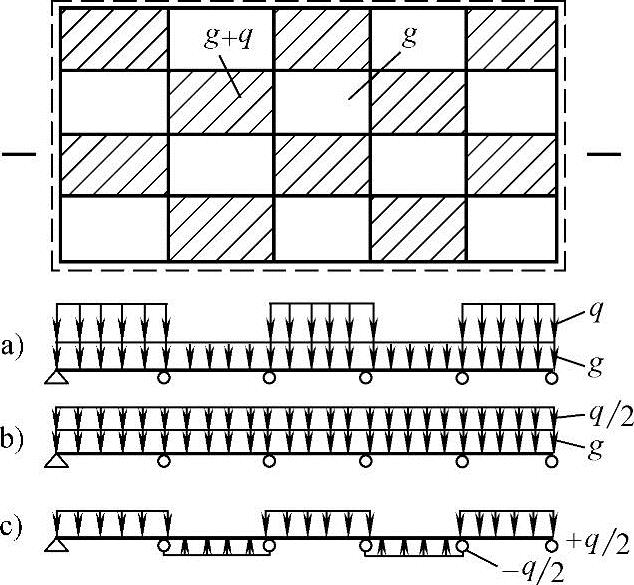
图2.16-4 双向板活荷载最不利布置图
在反对称荷载±q/2作用下，所有中间支座可视为简支边。如果边支座亦为简支，则所有区格板均为四边简支板，很容易利用表格求得反对称荷载作用下当μ=0时各区格板的跨中最大弯矩。
最后按式（2.16-20）、式（2.16-21）计算出两种荷载情况的实际跨中弯矩，并进行叠加，即可求得各区格板跨中最大正弯矩，即
mxμ=mx+μmy （2.16-20）
myμ=my+μmy （2.16-21）
其中，μ=0.2。
2）支座最大弯矩：为了简化计算，可假定全板各区格满布活荷载时支座弯矩最大。这样，对内区格可按四边固定的单跨双向板计算其支座弯矩。至于边区格，其边支座边缘条件按实际情况考虑，内支座按固定边考虑，计算其支座弯矩。
2.按塑性理论计算双向连续板
按塑性理论计算双向连续板，目前常用的计算方法有塑性铰线法、板带法以及电子计算机进行分析的最优配筋法等。
3.双向板的截面设计和配筋构造
（1）截面设计 双向板的厚度一般在80～160mm范围内，任何情况下不得小于80mm，同时为了满足刚度要求对于简支板不小于lx/45，对于连续板不小于lx/50。
对于四边与梁整体连接的双向板，除角区格外，考虑周边支承梁对板的推力的有利影响，不论按弹性理论还是按塑性理论计算方法得到的弯矩或配筋均可按下述规定予以折减：
对于连续板的中间区格的跨中截面及中间支座折减系数为0.8。
对于边区格的跨中截面及从楼板边缘算起的第二支座截面：
当lb/l＜1.5时，折减系数为0.8；
当1.5≤lb/l≤2时，折减系数为0.9。
这里lb是沿楼板边缘方向的计算跨度，l是垂直于楼板边缘方向的计算跨度。
对于角区格的各截面，不应折减。
跨中沿短边方向（弯矩较大方向）的板底钢筋宜放在沿长边方向板底钢筋的下面，板面钢筋则相反。计算时在两个方向应采用各自的有效高度h0。
（2）钢筋的配置 将板在lx及ly方向各分为三个带（图2.16-5），两边带的宽度各为较小跨度lx的1/4，其余则为中间带。在中间带内按最大正弯矩求得的板底钢筋均匀配置，边带内则减少50%，但每米宽度内不得少于3根。对于支座边缘负弯矩钢筋，为了承受板四角的扭矩，按支座最大负弯矩求得的钢筋沿全支座宽度均匀分布，不能在边带内减少。
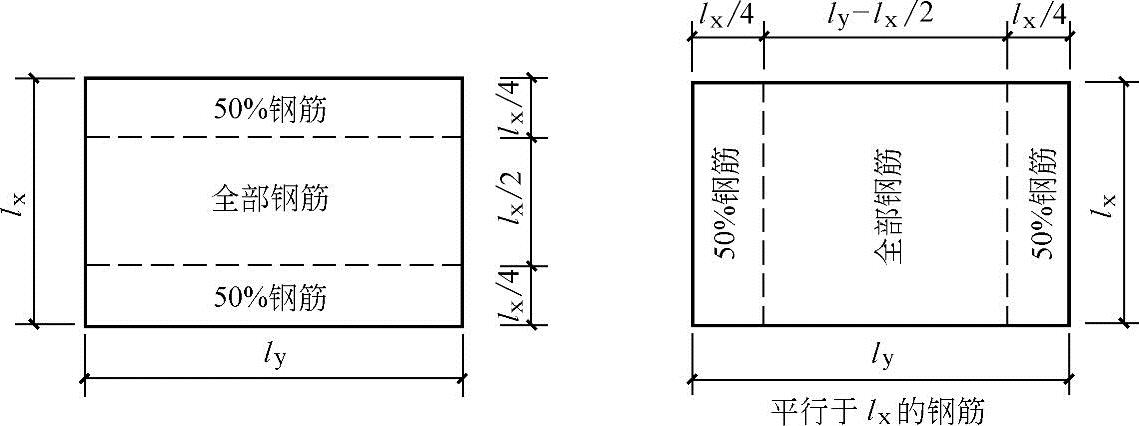
图2.16-5 钢筋的配置
按塑性理论方法计算时，则根据计算假定，钢筋均匀分布。在简支的双向板中，考虑到计算时未计及支座的部分嵌固作用，故每个方向的正弯矩钢筋均应弯起1/3；在固定支座及连续的双向板中，板底正弯矩钢筋可弯起1/2作为支座负弯矩钢筋，不足时则另外配置板顶直筋。
沿墙边及墙角的板顶构造钢筋与单向板肋梁楼盖中相同。
4.支承双向板的梁设计
不论双向板采用弹性理论还是塑性铰线法计算，都可从每一区格的四角作45°线与平行于长边的中线相交，把整块板分成四小块，每小块的恒载和活载传至相邻的支承梁上（图2.16-6），故短边支承梁上承受三角形荷载，长边支承梁上承受梯形荷载，支承梁自重仍为均布荷载。
支承梁的内力可按弹性理论或考虑塑性内力重分布的调幅法计算。
（1）按弹性理论计算 对于等跨或近似等跨（跨度相差不超过10%）连续梁承受三角形或梯形荷载下的内力，可直接从有关设计手册中查出内力系数，也可按等效均布荷载来计算。
等效均布荷载是按支座弯矩相等的条件来确定的，三角形分布荷载和梯形分布荷载化为等效均布荷载的计算公式如图2.16-7所示。
（2）按调幅法计算 按调幅法计算双向板支承梁时，各支座和跨中的弯矩设计值可取为
M=λM0 （2.16-22）
式中 M0——相应简支梁的跨中最大弯矩；
λ——系数，边跨中和第一内支座取λ=0.7，中间跨跨中和中间跨支座取λ=0.5。
各跨梁端剪力可取为
V=λ′R0 （2.16-23）
式中 R0——相应简支梁的支座反力；
λ′——系数，边跨边支座取λ′=0.8，边跨内支座取λ′=1.2，中间跨各支座均取λ′=1.0。
图2.16-6 支承双向板梁的荷载
图2.16-7 等效荷载
【例2.16-1】 某钢筋混凝土现浇肋形楼盖的次梁，跨中承受最大正弯矩设计值M=115kN·m。混凝土强度等级为C30，纵向受拉钢筋采用热轧HRB400钢筋。楼板厚度h′f=80mm，次梁高度h=450mm，宽度b=200mm，纵向受拉钢筋合力点至混凝土边缘的距离as=40mm。
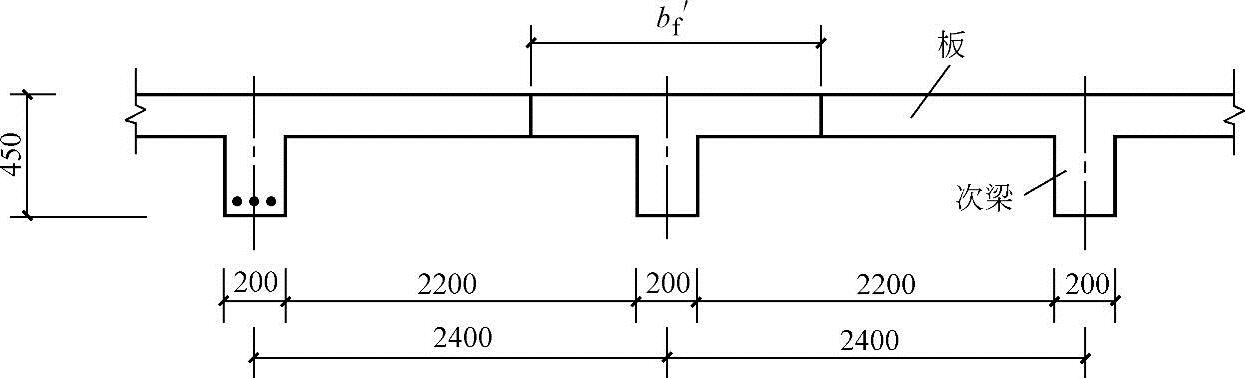
图 2.16-8
1.若已知次梁的计算跨度l0=6m，间距为2.4m，净距sn=2.2m，如图2.16-8所示，则翼缘的计算宽度b′f与（ ）项数值最为接近。
（A）2000mm （B）2400mm （C）1800mm （D）2200mm
答案：（A）
解答：按梁跨度l0考虑：b′f=l0/3=2000mm
按梁净距考虑：b′f=b+sn=（200+2200）mm=2400mm
按翼缘高度考虑：
，因此对于肋形楼盖梁不受此要求限制。因此翼缘计算宽度b′f=2000mm
2.若已知翼缘计算宽度b′f=1800mm，按单筋T形截面计算的次梁跨中所需受拉钢筋计算截面面积与（ ）项数值最为接近。
（A）1009mm2 （B）1033mm2 （C）944mm2 （D）1124mm2
答案：（C）
解答：混凝土强度等级C30，fcu，k=30.0N/mm2fc=14.3N/mm2ft=1.43N/mm2
钢筋强度：fy=f′y=360N/mm2Es=200000N/mm2
弯矩值：M=115kN·m
截面类型鉴别：
属于第一类T形截面，即可按宽度为b′f的矩形截面计算。
混凝土截面受压区高度x为
则纵向受拉钢筋的面积为
选3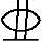
20，As=942mm2
配筋率
受弯纵筋最小配筋率
ρmin=max{0.20%，0.45ft/fy}=max{0.20%，0.18%}=0.20%＜ρ=1.15%
有关全国一、二级注册结构工程师专业考试教程的文章
- 详细阅读
-
2.16.1单向板肋梁楼盖的专业教程详细阅读
表2.16-1 连续板、梁的计算跨度续）荷载1）折算荷载：为了考虑支座抵抗转动的影响，目前一般采用增大恒载和相应地减小活荷载的办法来处理，即以折算荷载来代替实际计算荷载。3）处于重要部位，而又要求有较大强度储备的构件，如肋梁楼盖中的主梁。对跨度差别小于10%的不等跨连续板和次梁，仍可采用式和式（2.16-......
2023-08-28
-
混凝土结构设计-单向板肋梁楼盖截面设计与构造详细阅读
当板厚较大时，可设置马凳筋作为防范措施。2）连续单向板的配筋方案。连续单向板除了按计算配置受力钢筋，还应按构造配置以下五种钢筋。该钢筋平行于单向板的长跨，放在正、负受力钢筋的内侧。③与主梁垂直的上部构造筋。板在靠近墙体处由于墙体的嵌固作用而产生负弯矩，因此应在板内沿墙体设置承受负弯矩作用的上部构造钢筋。......
2023-08-30
-
肋梁楼盖荷载传递原则-混凝土结构设计详细阅读
图2-3 交叉梁的荷载传递图2-4 荷载传递原则a）EI1=EI2时，P1/P和P2/P随跨度比L2/L1的变化 b）L1=L2时，P1/P和P2/P随抗弯刚度比EI1/EI2的变化2.单向板与双向板首先考虑图2-5a所示仅两对边简支的矩形板。根据上述荷载传递原则，板面荷载沿板短跨方向传递程度要大于沿长跨方向的传递程度。......
2023-08-30
-
混凝土结构设计指南：2.3.5双向板支承梁设详细阅读
对于等跨或近似等跨的连续支承梁，可先将支承梁的三角形或梯形分布荷载化为等效均布荷载，再利用均布荷载下等跨连续梁的计算表格来计算梁的内力。图2-47 双向板传给支承梁的荷载图2-48 三角形及梯形荷载转换为等效均布荷载按等效均布荷载求出支座弯矩后，再根据求得的支座弯矩和每跨的实际荷载分布，由各跨平衡条件计算出跨中弯矩和支座剪力。......
2023-08-30
-
双向板截面设计与构造要点详细阅读
3）角区格板截面弯矩值不予折减。对于多区格连续板支座截面负弯矩配筋在支座宽度范围内均匀设置。受力钢筋的直径、间距及弯起点、切断点的位置等规定，与单向板的有关规定相同。沿墙边、墙角处的构造钢筋与单向板相同。......
2023-08-30
- 详细阅读
-
混凝土结构设计：2.4.2井字梁楼盖结构详细阅读
单跨简支或多跨连续的井字梁楼盖梁板有时可采用有外伸悬挑的网格梁。图2-51 井字梁楼盖的平面布置图2-52 三向网格梁2.井字梁的间距两个方向井字梁的间距可以相等，也可以不相等。井字梁楼盖一般采用现浇梁板。由于井字梁避开了柱位，靠近柱位的区格板需另作加强处理。但这种情况下的井字梁受力复杂，宜采用电算。......
2023-08-30
相关推荐