然而,配筋率加大对提高截面弯曲刚度并不显著,因此就有可能出现不满足挠度验算的要求。对此,可以给出不需做挠度验算的最大跨高比。图7.14梁端支撑处转角过大引起的问题②防止对结构构件产生不良影响。③防止对非结构构件产生不良影响。例如,防止梁、板明显下垂引起的不安全感,防止可变荷载引起的振动及噪声产生的不良感觉等。调查表明,从外观要求来看,构件的挠度宜控制在l0/250的限值以内。......
2023-09-19
1.挠度验算
变形验算属于正常使用极限状态验算,如果结构构件的变形过大,将影响结构的使用功能,并且人们的心理也无法承受。所以要对构件的变形进行限制。

式中,S为与荷载类型、支承条件有关的系数;EI是梁的截面抗弯刚度;l0是梁的计算跨度。用B表示梁的截面抗弯刚度EI,式(2.11-37)可表示为

例如,对于承受均布荷载的简支梁,S=5/48,即
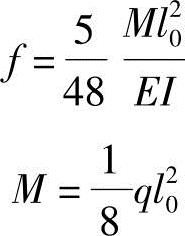
式中 q——简支梁所承受的均布荷载。
最小刚度原则:在等截面构件中,可假定各同号弯矩区段内的刚度相等,并取用该区段内最大弯矩处的刚度。当计算跨度内的支座截面刚度不大于跨中截面刚度的2倍或不小于跨中截面刚度的1/2时,该跨也可按等刚度构件进行计算,其构件刚度可取跨中最大弯矩截面的刚度。
2.按裂缝控制等级要求的荷载组合作用下受弯构件的短期刚度Bs
(1)钢筋混凝土受弯构件的短期刚度为
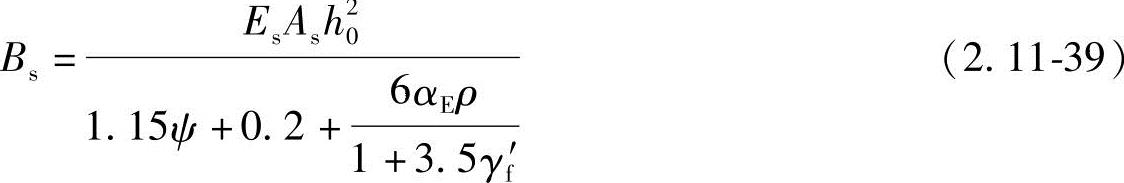
式中 ψ——裂缝间纵向受拉普通钢筋应变不均匀系数,按式(2.11-6)计算;
αE——钢筋弹性模量与混凝土弹性模量之比,αE=Es/Ec;
ρ——纵向受拉钢筋配筋率,对钢筋混凝土受弯构件,取为As/(bh0);对预应力混凝土受弯构件,改为(α1Ap+As)/(bh0),对灌浆的后张预应力筋,取α1=1.0,对无粘结后张预应力筋,取α1=0.3;
γf′——受压翼缘截面面积与腹板有效截面面积的比值,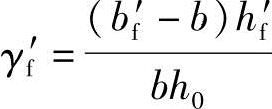 。
。
(2)预应力混凝土受弯构件
1)要求不出现裂缝的构件
Bs=0.85EcI0 (2.11-40)
2)允许出现裂缝的构件

式中 kcr——预应力混凝土受弯构件正截面的开裂弯矩Mcr与弯矩Mk的比值,当kcr>1.0时,取kcr=1.0;
σpc——扣除全部预应力损失后,由预加力在抗裂验算边缘产生的混凝土预压应力;
γ——混凝土构件的截面抵抗矩塑性影响系数;
γm——混凝土构件的截面抵抗矩塑性影响系数基本值,可按正截面应变保持平面的假定,并取受拉区混凝土应力图形为梯形、受拉边缘混凝土极限拉应变为2ftk/Ec确定;对常用的截面形状,γm值可按表2.11-3取用;
h——截面高度(mm):当h<400时,取h=400;当h>1600时,取h=1600;对圆形、环形截面,取h=2r,此处,r为圆形截面半径或环形截面的外环半径。
对预压时预拉区出现裂缝的构件,Bs应降低10%。
表2.11-3 截面抵抗矩塑性影响系数基本值γm
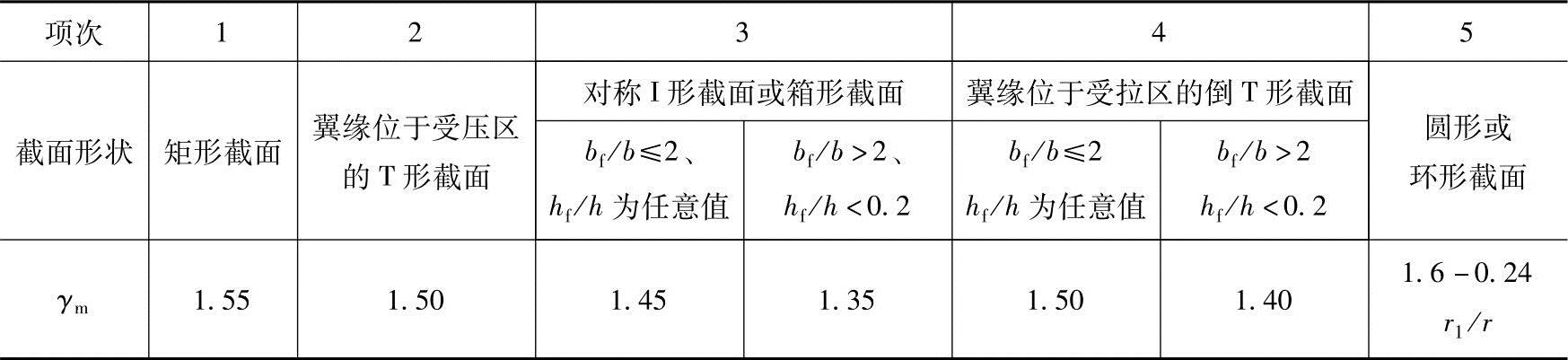
注:1.对b′f>bf的Ⅰ形截面,可按项次2与项次3之间的数值采用;对b′f<bf的Ⅰ形截面,可按项次3与项次4之间的数值采用。
2.对于箱形截面,b系指各肋宽度的总和。
3.r1为环形截面的内半径,对圆形截面取r1为零。
3.受弯构件的刚度B
矩形、T形、倒T形和I型截面受弯构件考虑荷载长期作用影响的刚度B可按下列规定计算:
(1)采用荷载标准组合时

(2)采用荷载准永久组合时

式中 Bs——短期刚度,按式(2.11-39)或式(2.11-40)或式(2.11-41)计算;
Mk、Mq——按荷载的标准组合及准永久组合计算的弯矩值,取计算区段内的最大弯矩值;
θ——考虑荷载长期作用对挠度增大的影响系数,θ可按下列规定取用:
1)钢筋混凝土受弯构件
当ρ′=0时,取θ=2.0;当ρ′=ρ时,取θ=1.6;当ρ′为中间数值时,θ按线性内插法取用。此处,ρ′=A′s/(bh0),ρ=As/(bh0)。
对翼缘位于受拉区的倒T形截面,θ应增加20%。
2)预应力混凝土受弯构件,取θ=2.0。
《混凝土结构设计规范》规定受弯构件的挠度应按荷载标准组合或准永久组合并考虑荷载长期作用影响的刚度B进行计算,所求得的挠度计算值不应超过表2.1-1规定的限值。
f≤[f] (2.11-49)
【例2.11-4】 已知在教学楼楼盖中一矩形截面简支梁,截面尺寸为200mm×500mm,配置3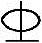 20受力钢筋,混凝土强度等级为C20,cs=25mm,l0=5.6m;承受均布荷载,其中永久荷载(包括自重在内)标准值gk=12.4kN/m,楼面活荷载标准值qk=8kN/m,楼面活荷载的准永久值系数ψq=0.5。试验算其挠度f。
20受力钢筋,混凝土强度等级为C20,cs=25mm,l0=5.6m;承受均布荷载,其中永久荷载(包括自重在内)标准值gk=12.4kN/m,楼面活荷载标准值qk=8kN/m,楼面活荷载的准永久值系数ψq=0.5。试验算其挠度f。
解答:
1.求Mq
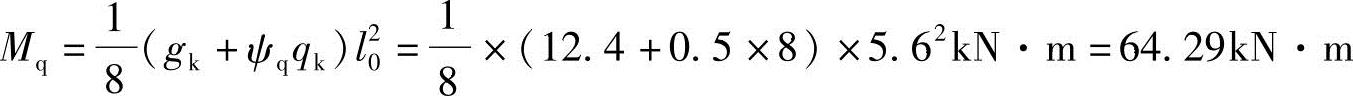
2.计算有关参数
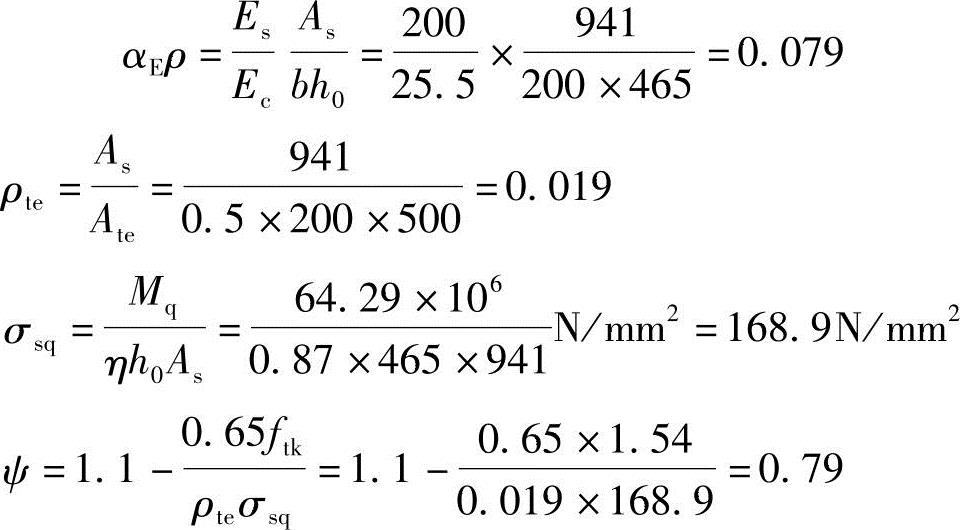
3.计算Bs
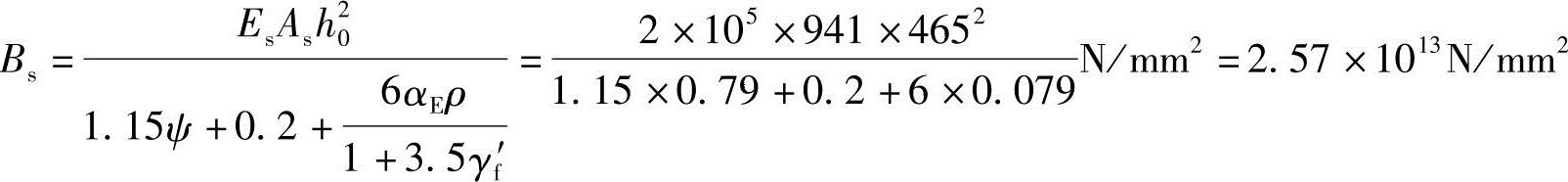
4.计算B
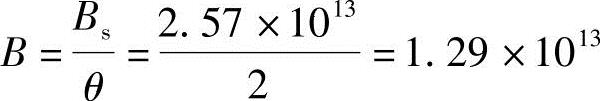
5.变形验算
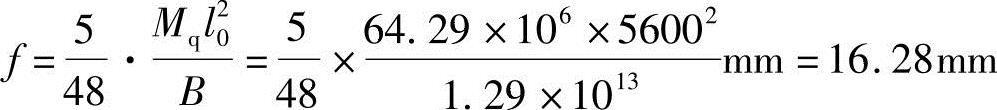
查附表可知,[f/l0]=1/200
f/l0=16.28/5600=1/344<1/200,故变形满足要求。
【例2.11-5】 钢筋混凝土空心楼板截面尺寸为120mm×860mm(图2.11-4a),计算跨度l0为3.48m,板承受自重、抹面重量及楼面均布活荷载,跨中按荷载效应准永久组合计算的弯矩值Mq为3406.1N·m,混凝土强度等级为C20,根据正截面承载力的计算,配置钢筋为9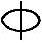 8(HPB300),As=452mm2,板的挠度限值为l0/200。试验算该板的挠度。
8(HPB300),As=452mm2,板的挠度限值为l0/200。试验算该板的挠度。
解答:先将原孔按等面积、同形心轴位置和对形心轴惯性矩不变的原则折算成矩形孔(图2.11-4b),即
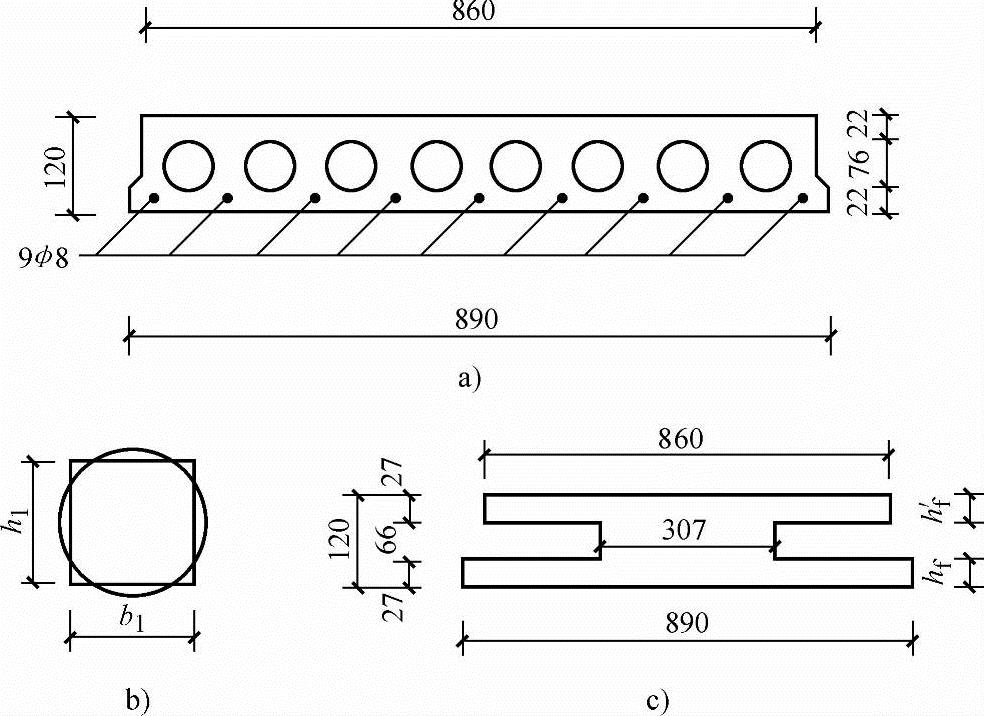
图2.11-4 【例2.11-5】图
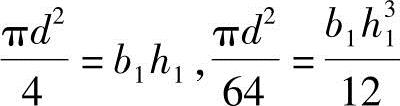
求得b1=0.91d,h1=0.87d,折算后的工字型截面尺寸如图2.11-4c所示,则由式(2.11-11):
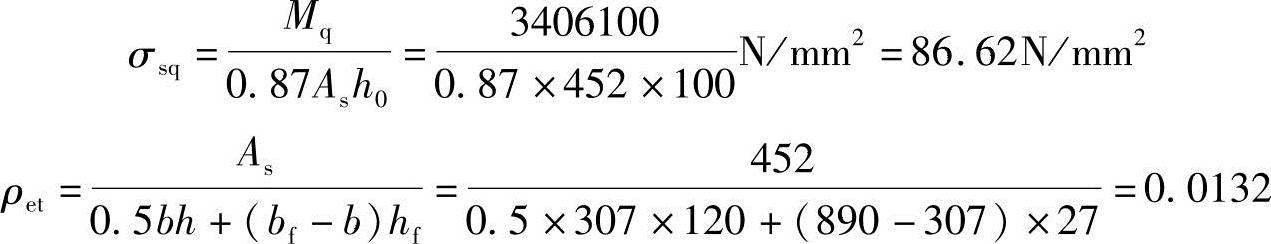
由式(2.11-6)
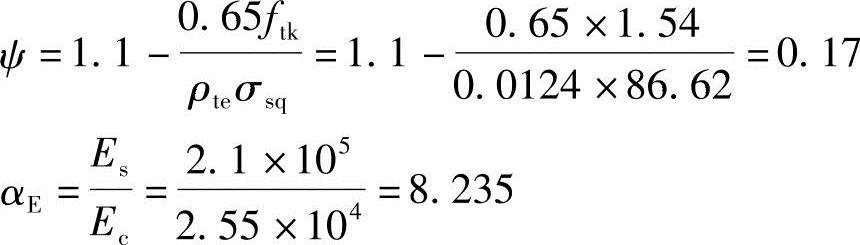
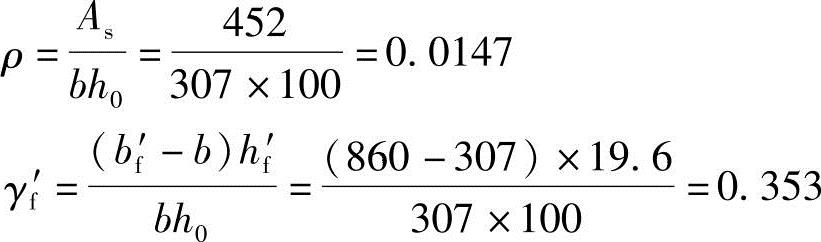
(因hf′=27mm>0.2h0=19.6mm,故取hf′=19.6mm)
由式(2.11-39)得荷载效应标准组合下的短期刚度为
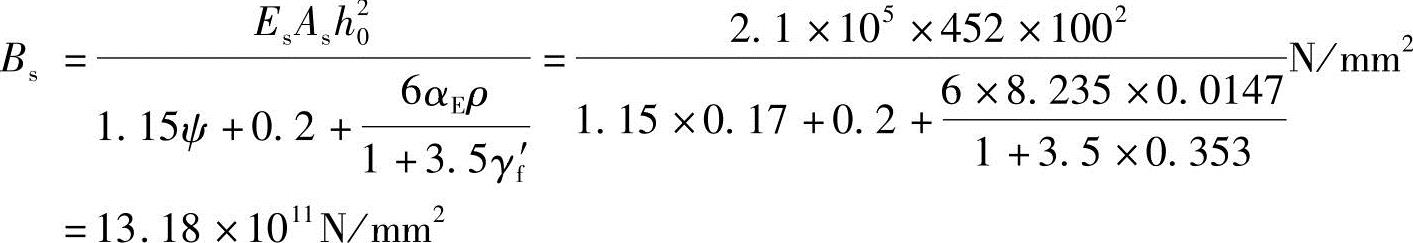
因ρ′=0,故θ=2
由式(2.11-48)得,在荷载效应准永久组合下并考虑荷载长期作用影响的刚度为
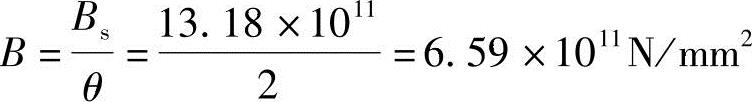
跨中最大挠度为
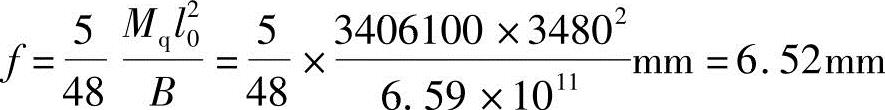
f/l0=6.52/3480=1/533.7<1/200,故变形满足要求。
有关全国一、二级注册结构工程师专业考试教程的文章

然而,配筋率加大对提高截面弯曲刚度并不显著,因此就有可能出现不满足挠度验算的要求。对此,可以给出不需做挠度验算的最大跨高比。图7.14梁端支撑处转角过大引起的问题②防止对结构构件产生不良影响。③防止对非结构构件产生不良影响。例如,防止梁、板明显下垂引起的不安全感,防止可变荷载引起的振动及噪声产生的不良感觉等。调查表明,从外观要求来看,构件的挠度宜控制在l0/250的限值以内。......
2023-09-19

5.6.3.1 持力层承载力验算持力层即直接承受基础上部荷载的地层,按照前述5.3.2节中基底压力的计算方法可以确定出由于上部荷载、基础本身自重和上覆填土自重在基底产生的基底压力,再按照上述方法确定持力层地基承载力特征值,在进行持力层承载力验算时,《规范》规定:基础底面的压力,应符合下式要求。......
2023-08-28

混凝土在硬化期间和使用过程中,因受物理、化学和力学因素的影响产生变形,这些变形是使混凝土产生裂缝的重要原因之一,从而影响混凝土的强度和耐久性。混凝土的湿胀变形量很小,一般无破坏作用。从图4.13可以看出,混凝土的变形模量随应力的增加而减小。图4.15混凝土的变形与荷载作用时间关系混凝土受荷后立即产生瞬时变形,随着荷载持续作用时间的延长,又产生徐变变形。......
2023-09-01

在E1和E2地震作用下,各类城市桥梁的抗震验算目标应满足表7.8-2的要求。采用非线性时程进行地震反应分析的桥梁可按式验算转角。图7.8-4 等效屈服曲率......
2023-08-28

提示:圆形截面对中性轴的面积矩S=0.212πd3/8。见《建筑地基基础设计规范》表8.1.2注4,超过300kPa时应进行抗剪验算。根据《建筑地基基础设计规范》表3.0.1,地基基础设计等级为丙级,根据第3.0.2条及表3.0.2,框架结构大于5层时应进行地基变形验算。题6~10:某多层框架结构厂房柱下矩形独立基础,柱截面为1.2m×1.2m,基础宽度为3.6m,抗震设防烈度为7度,设计基本地震加速度为0.15g。......
2023-08-25

有些期刊对论文结构的规定比较弹性,作者可以根据论文内容的需要、按照论文所要说明的问题的特点采用结构变形Ⅲ,把不同的研究方法,或者把不同的研究结果及相应的讨论按照思维论证的逻辑列为各具主标题的几个部分。图3-3示意说明分层次的研究结果/讨论的情况,其中每一研究结果/讨论部分都有各自的主标题。......
2023-07-08

图1.4隧道挤压变形破坏围岩扰动范围大兰渝铁路挤压性围岩隧道开挖后塑性区迅速扩大,特别是当支护不及时或结构刚度、强度不够时,围岩扰动范围更大。新城子隧道松动圈测试结果表明,未扰动区基本位于开挖临空面向里15 m以外的位置,因此一般锚杆长度很难锚固到稳定围岩。......
2023-09-21
相关推荐