首页理论教育2.5.3大偏心受拉构件正截面承载力计算|结构工程师考试教程

2.5.3大偏心受拉构件正截面承载力计算|结构工程师考试教程

2023-08-28 理论教育版权反馈

【摘要】：当纵向拉力作用在As合力点以外时，属于大偏心受拉构件。图2.5-3所示为矩形截面大偏心受拉构件的受力情况。图2.5-3 大偏心受拉构件承载力计算图在设计时为了使钢筋总用量最少，与偏心受压构件一样，应取受压区高度x=ξbh0，代入式及式可得若按式求得的As′＜ρminbh，则可先按构造要求或最小配筋率配置As′，变为已知As′求As的情况。

当纵向拉力作用在A_s合力点以外时，属于大偏心受拉构件。

图2.5-3所示为矩形截面大偏心受拉构件的受力情况。构件破坏时钢筋A_s及A_s′应力都达到屈服强度，受压区混凝土应力取用α₁f_c，应力分布按矩形图计算，则由内力平衡条件得

N≤f_yA_s-f_y′A_s′-α₁f_cbx （2.5-2）

图2.5-2 轴心受拉构件

上述公式的适用条件为x≤ξ_bh₀及x≥2a_s′。

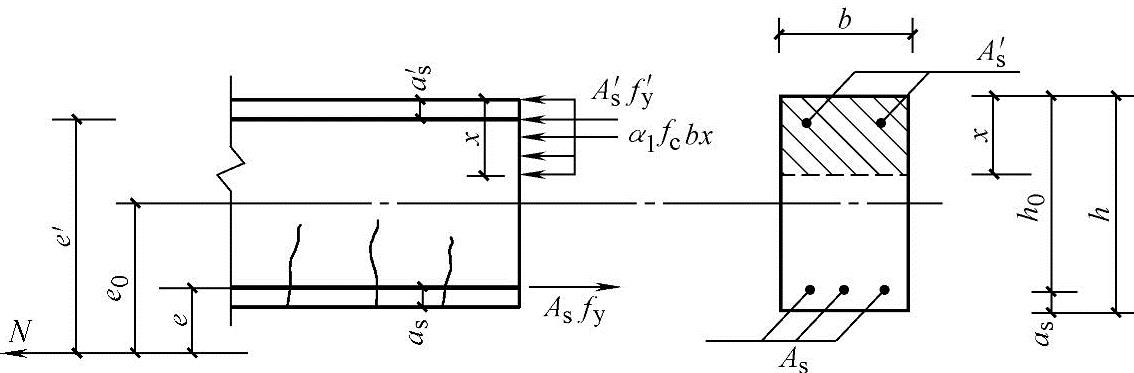
图2.5-3 大偏心受拉构件承载力计算图

在设计时为了使钢筋总用量（A_s+A_s′）最少，与偏心受压构件一样，应取受压区高度x=ξ_bh₀，代入式（2.5-3）及式（2.5-2）可得

若按式（2.5-5）求得的A_s′＜ρ_minbh（包括为负值），则可先按构造要求或最小配筋率配置A_s′，变为已知A_s′求A_s的情况。

当已知A_s′求A_s时，可由式（2.5-3）求出αs

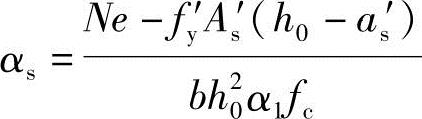
然后用下式求出ξ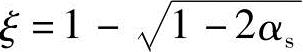

x=ξh₀，当2a_s′≤x≤ξ_bh₀，则由式（2.5-2）可求出As

式（2.5-7）与偏心受压构件计算公式相比，仅是N变为“+”号，由于轴向拉力的存在增加了受拉钢筋的数量。

若x＜2a_s′，可以近似地假定受压区混凝土承担的压力与受压钢筋承担的压力重合，则对受压钢筋合力中心取矩可得：

式中 e′——轴向拉力N作用点到受压钢筋A_s′的距离。

由式（2.5-8）得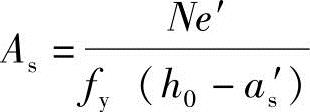

当构件的截面尺寸、材料和纵向钢筋均为已知，要复核截面的承载力时，可联立式（2.5-2）、式（2.5-3）求解，先解出x，根据x值的大小，来决定N值的解法。当2a_s′≤x≤ξ_bh₀时，用式（2.5-2）求N；当x＜2a_s′时，用式（2.5-8）求N。

当采用对称配筋时，由于A_s=A_s′，f_y=f_y′，代入式（2.5-2）后，求得的x值必为负值，属x＜2a_s′的情况，则可用式（2.5-8）进行配筋计算或承载力校核。