首页理论教育单筋矩形截面正截面受弯承载力计算方法

单筋矩形截面正截面受弯承载力计算方法

2025-09-30 理论教育版权反馈

【摘要】：单筋矩形截面正截面受弯承载力计算简图如图2.3-5所示。图2.3-5 单筋矩形截面正截面受弯承载力计算简图经济配筋率的范围为：板 ρ=0.4%～0.8%矩形梁 ρ=0.6%～1.5%T形梁 ρ=0.9%～1.8%。一矩形截面简支梁承受弯矩设计值M=230kN·m，采用C20级混凝土，fc=9.6MPa，HRB400级钢筋，fy=360MPa。

1.基本公式及适用条件

（1）基本公式。单筋矩形截面正截面受弯承载力计算简图如图2.3-5所示。由力的平衡关系可得：

α₁f_cbx=A_sf_y （2.3-5）

由力矩平衡可得：

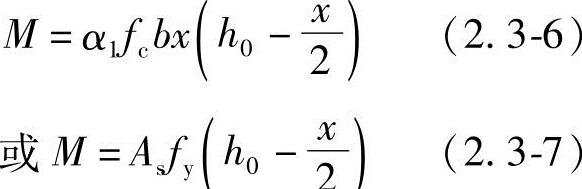
（2）适用条件

ξ≤ξ_b

或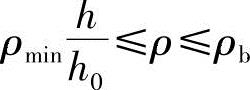

《混凝土结构设计规范》（GB 50010—2010）规定ρ_min应取0.2%和45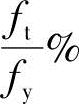中的较大值。

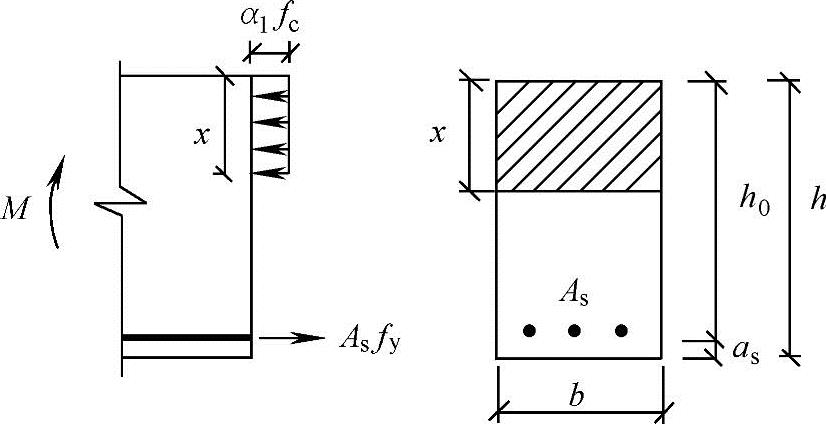
图2.3-5 单筋矩形截面正截面受弯承载力计算简图

经济配筋率的范围为：

板 ρ=0.4%～0.8%

矩形梁 ρ=0.6%～1.5%

T形梁 ρ=0.9%～1.8%（相对于腹板）。

2.单筋矩形截面配筋设计

根据式（2.3-5）、式（2.3-6）或式（2.3-7）就可以进行截面配筋设计。为了设计方便，式（2.3-6）、式（2.3-7）可写成：

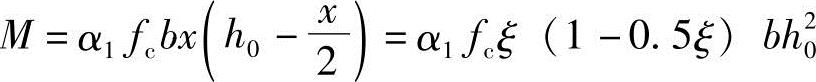
M=A_sf_yh₀ （1-0.5ξ）

令 α_s=ξ（1-0.5ξ）（2.3-8）

γ_s=1-0.5ξ （2.3-9）

则 M=α₁α_sf_cbh²₀ （2.3-10）

或 M=A_sf_yγ_sh₀ （2.3-11）

截面配筋设计时经常遇到以下两种情况：

（1）已知M、b、h、f_c、f_y、…，求A_s

解：①计算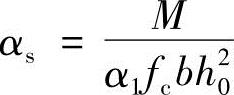

②计算ξ

由式（2.3-8）可得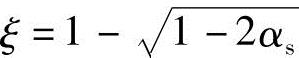，应不大于ξ_b

③计算配筋率ρ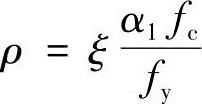，应满足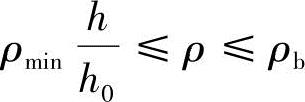

④计算A_s

A_s=ρbh₀

⑤绘制配筋图

设计时应尽量使受弯构件的配筋率落在经济配筋率范围之内，如按（4）计算的ρ值与经济配筋率相差较大也可重新选择b、h重复（1）～（4）。

（2）已知M、b、f_c、f_y、…，求A_s

解：①先假定ρ，使ρ落在经济配筋率范围之内。(https://www.chuimin.cn)

②根据配筋率ρ与ξ的关系求ξ

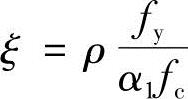
③计算α_s

α_s=ξ（1-0.5ξ）

④由式（2.3-10）求h₀

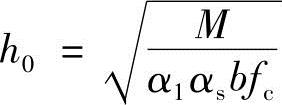
⑤计算h

h=h₀+a_s

计算出的h取整后（宜符合模数），变为已知b、h求A_s的情况。当实际取的h值大于由第5步计算的h值时也可不必重新计算而直接取A_s=ρbh₀。

【例2.3-1】一矩形截面简支梁b×h=200mm×500mm，计算跨度l=6m，承受均布活荷载标准值q_k=12kN/m，均布恒荷载标准值g_k=10kN/m（不含自重），结构安全等级为二级，试进行截面配筋设计。

解答：选C30级混凝土，f_c=14.3MPa；HRB400级钢筋，f_y=360MPa。结构安全等级为二级，γ₀=1.0。恒载分项系数γ_G=1.2；活载分项系数γ_Q=1.4。

梁自重标准值 g_k′=25×0.2×0.5×1kN/m=2.5kN/m（钢筋混凝土容重取25kN/m³）

简支梁跨中弯矩设计值：

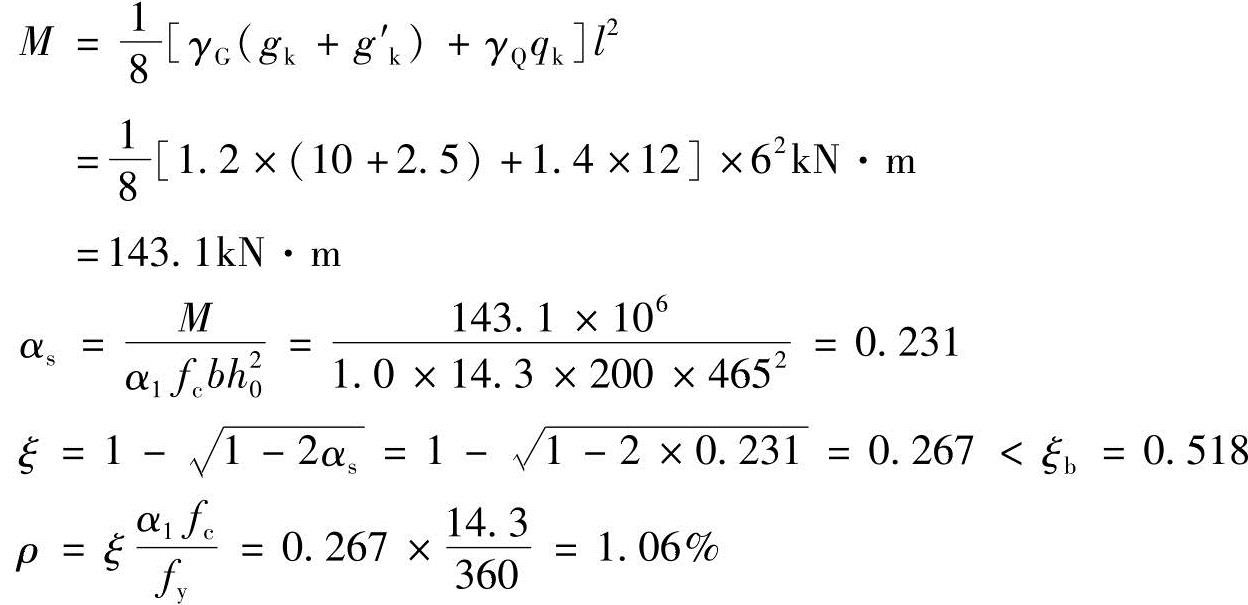
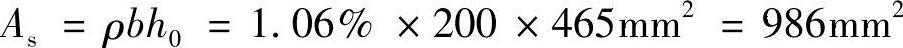，实配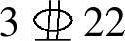，A_s=1140mm²。

如图2.3-6所示。

【例2.3-2】一矩形截面简支梁承受弯矩设计值M=230kN·m，采用C20级混凝土，fc=9.6MPa，HRB400级钢筋，f_y=360MPa。试确定梁截面尺寸及配筋。

解答：选b=250mm，假设ρ=1%

则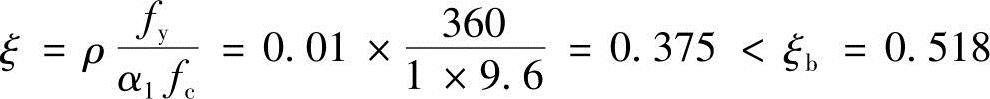

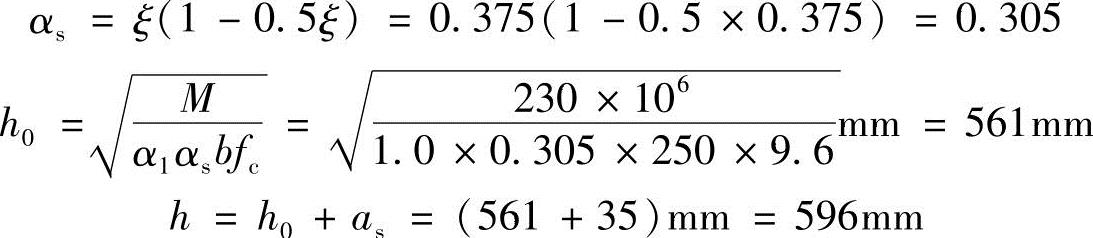
实取h=600mm。

因实际所取梁高与设计所取梁高相差很小，故不必按b×h=200mm×600mm重新计算A_s，而可直接取A_s=ρbh₀=1%×250×565mm²=1413mm²。实配3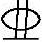25，A_s=1473mm²

如果实际选取梁高（宜符合模数）与计算梁高相差较大，则应按已知b、h的情况求A_s。

【例2.3-3】已知一单跨简支板，板厚120mm，板上有30mm厚水泥砂浆找平层，板的计算跨度为4.2m，板上活荷载标准值q_k=2kN/m²，混凝土采用C30级，钢筋采用HPB300，试进行截面配筋。

解答：取板宽b=1000mm的板条作为计算单元。安全等级按二级考虑，γ₀=1.0

恒载分项系数γ_G=1.2；活载分项系数γ_Q=1.4

恒载标准值g_k=（1×1×0.12×25+1×1×0.03×20）kN/m=3.6kN/m

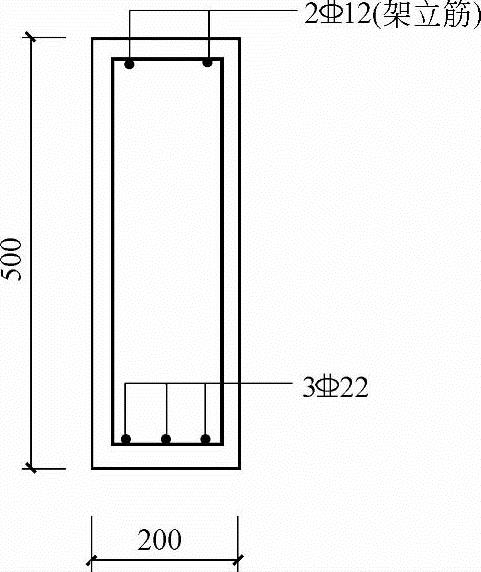
图2.3-6 配筋图

（钢筋混凝土容重取25kN/m³，砂浆容重取20kN/m³）

设计弯矩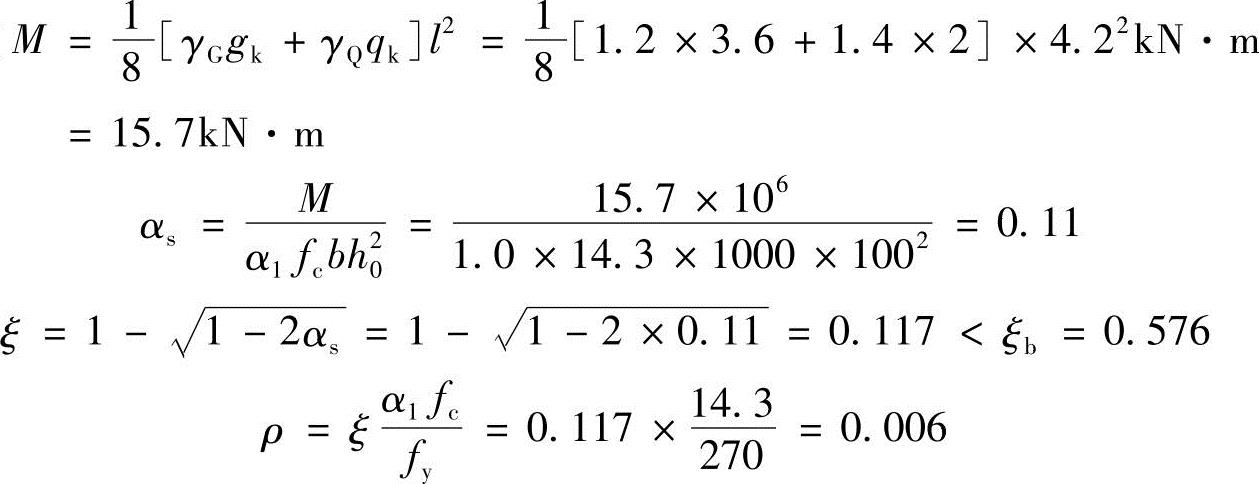

A_s=ρbh₀=0.006×1000×100mm²=600mm²。实配10@130，A_s=604mm²。构造筋选用8@200，如图2.3-7所示。

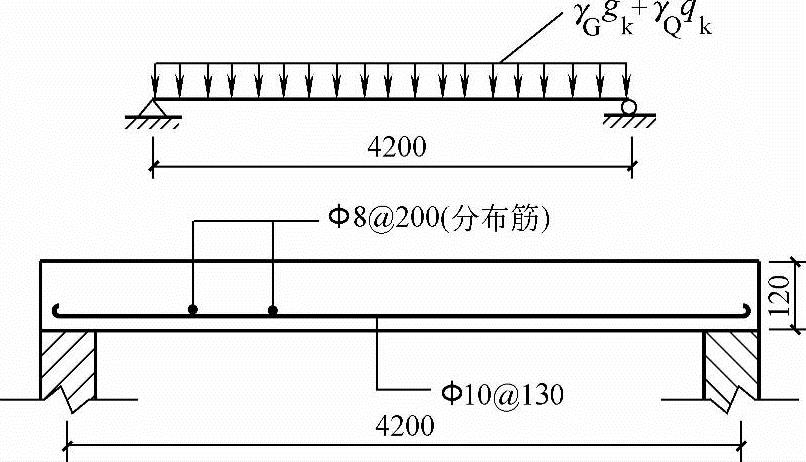
图2.3-7 简支板配筋图