首页理论教育受弯构件正截面承载力计算的基本假定-全国结构工程师考试教程

受弯构件正截面承载力计算的基本假定-全国结构工程师考试教程

2023-08-28 理论教育版权反馈

【摘要】：适筋梁与超筋梁的分界如图2.3-3中的界限破坏所示，即梁受拉钢筋屈服的同时受压区混凝土达到极限压应变。为便于设计，表2.3-1给出了相对界限受压区高度ξb的取值。图2.3-4 界限破坏时的应力图

1.基本假定

正截面承载力计算的基本假定包括：

（1）截面应变保持平面。

（2）不考虑混凝土的抗拉强度。

（3）混凝土受压的应力-应变关系已知。

目前我国现行《混凝土结构设计规范》所采用的钢筋、混凝土应力-应变关系如图2.3-1、图2.3-2所示。

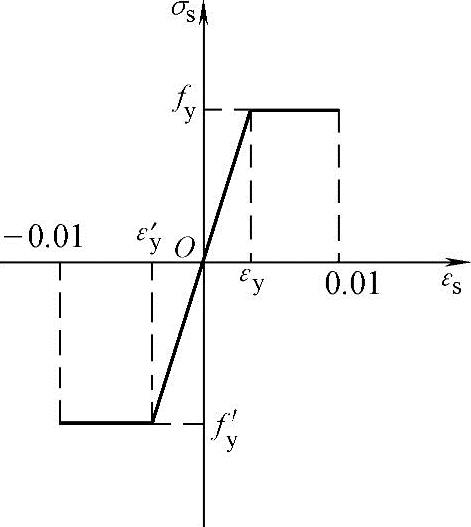
图2.3-1 钢筋应力-应变曲线

图2.3-2 混凝土应力-应变曲线

钢筋应力-应变关系采用理想的弹塑性本构关系，σ_s＜f_y时是弹性的，σ_s=f_y时是理想塑性的；混凝土的应力-应变曲线由两段组成。

当ε_c≤ε₀时

当ε₀＜ε_c≤ε_cuσ_c=f_c

式中 σ_c——混凝土压应变为ε_c时的混凝土压应力；

f_c——混凝土轴心抗压强度设计值；

ε₀——混凝土压应力达到f_c时的混凝土压应变，ε₀=0.002+0.5（f_cu，k-50）×10^-5，当计算的ε₀值小于0.002时，取为0.002；

ε_cu——正截面的混凝土极限压应变，当处于非均匀受压时，ε_cu=0.0033-（f_cu，k-50）×10^-5，如计算的ε_cu值大于0.0033，取为0.0033；当处于轴心受压时取为ε₀；

f_cu，k——混凝土立方体抗压强度标准值；

n——系数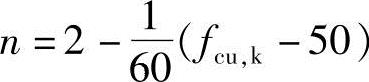，，当计算的n值大于2.0时，取为2.0。

2.适筋梁与超筋梁的分界

适筋梁与超筋梁的分界可用两种方式表达，即：ρ=ρ_b或ξ=ξ_b。

（1）相对界限受压区高度ξ_b。适筋梁与超筋梁的分界如图2.3-3中的界限破坏所示，即梁受拉钢筋屈服的同时受压区混凝土达到极限压应变。设钢筋屈服时的应变为ε_y，则。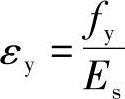

设界限破坏时中和轴高度为x_0b，则根据平截面假定可得：

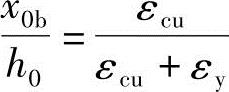
令x_b为界限破坏时等效矩形应力图形上的受压区高度，代入上式可得：

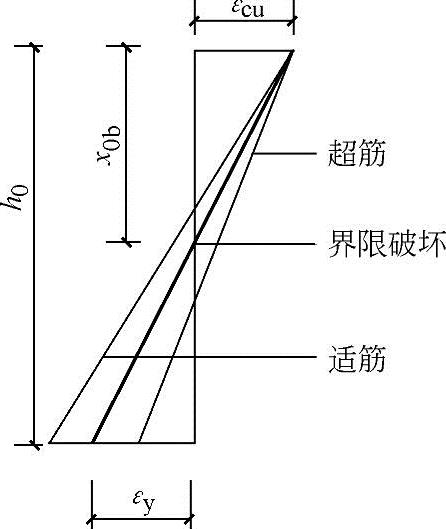
图2.3-3 适筋梁、超筋梁、界限配筋梁破坏时的正截面平均应变图

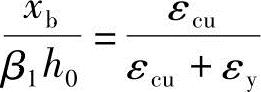
相对界限受压区高度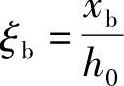，代入上式可得：

式中 f_y——钢筋抗拉强度设计值；

E_s——钢筋弹性模量；

ε_cu——非均匀受压时的混凝土极限压应变，混凝土强度等级小于等于C50时ε_cu=0.0033，大于C50时ε_cu=0.0033-（f_cu，k-50）×10^-5；

β₁——与混凝土强度相关的系数，当混凝土强度等级小于等于C50时β₁=0.8，C80时β₁=0.74，其间按线性内插法确定。

为便于设计，表2.3-1给出了相对界限受压区高度ξ_b的取值。

表2.3-1 相对界限受压区高度ξ_b取值

对于无明显屈服点的钢筋，钢筋的屈服应变由名义屈服应变代替（应考虑残余应变0.002的影响），即

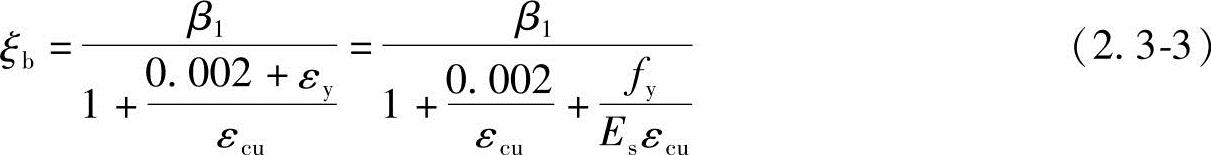
（2）界限配筋率ρ_b。界限配筋率即为适筋梁的最大配筋率，当ξ=ξ_b时所对应的配筋率ρ_b就是界限配筋率。ρ_b可以由图2.3-4力的平衡关系得出：

α₁f_cbx_b=A_sf_y=ρ_bbh₀f_y

所以

如果去掉脚标b就可得出适筋梁配筋率ρ与相对受压区高度的关系即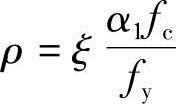。式中α₁的取值与混凝土强度等级有关，当混凝土强度等级不超过C50时，取α₁=1.0；当混凝土强度等级为C80时，取α₁=0.94，其间按线性内插法确定。

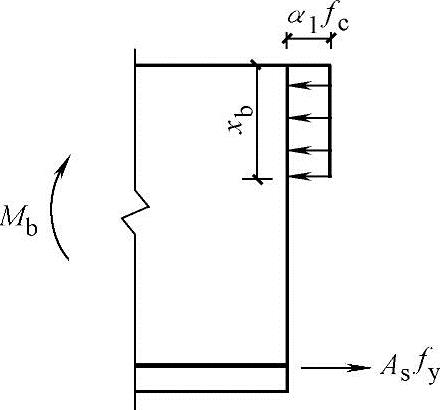
图2.3-4 界限破坏时的应力图