首页理论教育力法方程计算基本结构位移，图1.8-2和M1图适用

力法方程计算基本结构位移，图1.8-2和M1图适用

2023-08-28 理论教育版权反馈

【摘要】：原结构变为图1.8-1c，其中X1为多余约束中产生的约束力。图1.8-1 基本结构2.力法方程基本结构在B点的竖向位移必须为零，即δ11X1+Δ1p=0 式中，δ11为基本结构在X1=1作用下沿X1的指向引起的位移；Δ1p为基本结构在荷载P作用下沿X1的指向引起的位移。方程称为力法方程。但是，在力法分析中采用以下叠加公式计算M，即图1.8-2 Mp图和M1图上述公式对结构上的任何点均适用。

1.基本结构

对超静定结构，去掉多余约束，使原结构变成静定结构，这样形成的静定结构称为基本结构。如图1.8-1a去掉支座B的约束，就得到基本结构，如图1.8-1b所示。原结构变为图1.8-1c，其中X₁为多余约束中产生的约束力。

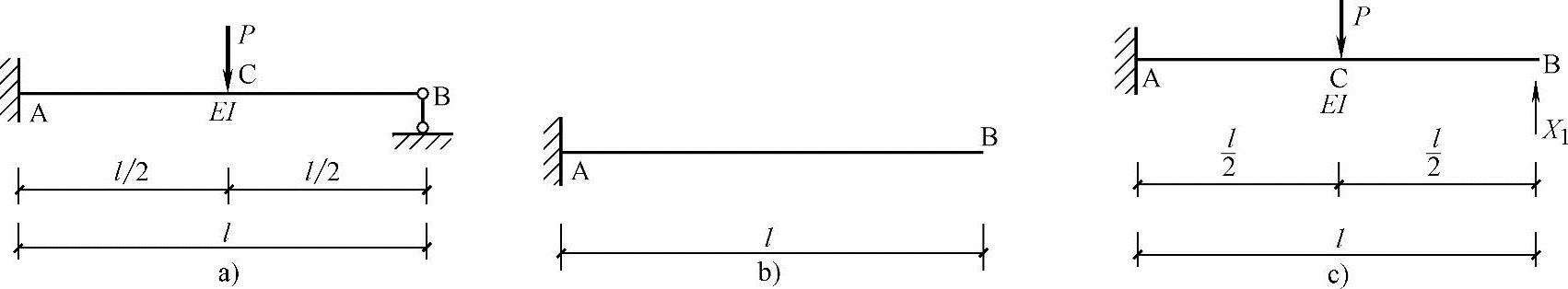
图1.8-1 基本结构

2.力法方程

基本结构在B点的竖向位移必须为零，即

δ₁₁X₁+Δ_1p=0 （1.8-1）

式中，δ₁₁为基本结构在X₁=1作用下沿X₁的指向引起的位移；Δ_1p为基本结构在荷载P作用下沿X₁的指向引起的位移。δ₁₁称为系数，Δ_1p称为自由项。方程（1.8-1）称为力法方程。

为计算系数和自由项，绘出M_p图和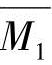图，如图1.8-2所示。应用图乘法求得

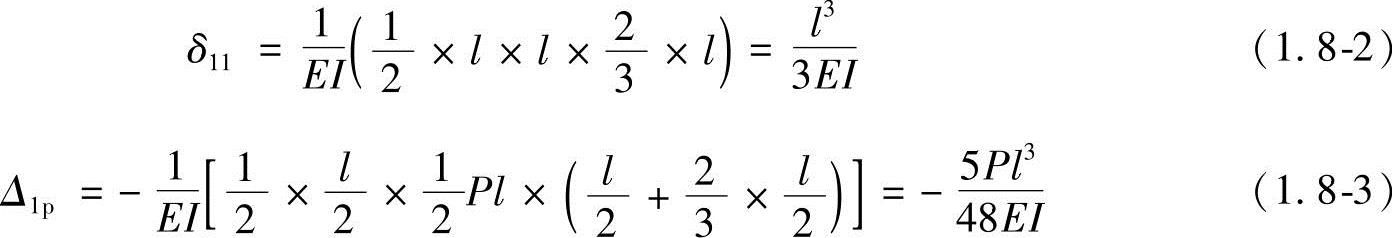
求解力法方程，得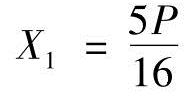（↑）。多余力X₁求得后，绘内力图，这是静定结构的计算问题。但是，在力法分析中采用以下叠加公式计算M，即

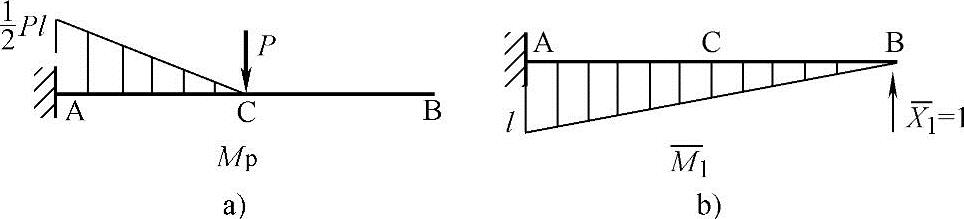
图1.8-2 M_p图和M₁图

上述公式对结构上的任何点均适用。先选定若干控制点，求出这些点上的M值，然后绘制M图。例如

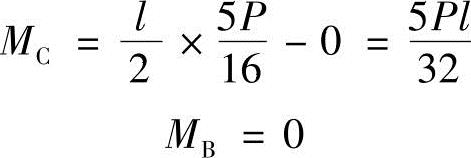
最后绘制M图，如图1.8-3所示。

3.力法典型方程

对于n次超静定结构，可去掉n个多余约束，得到静定的基本结构。将n个多余力视作附加荷载与原来的荷载一起加在基本结构上。利用n个多余约束处已知的位移条件，建立求n个多余力的力法方程，称为力法典型方程。

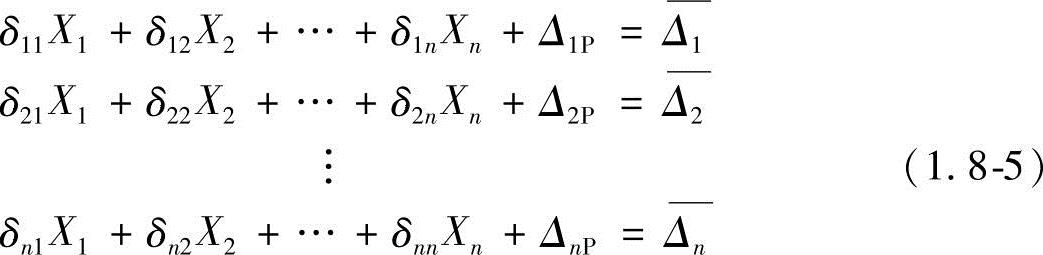
图1.8-3 M图

式中，δ_ii称为主系数（永远为正值），δ_ij（i≠j）称为副系数（可正可负），Δ_iP称为自由项。Δi为约束i处的已知位移。

显然，δ_ij=δ_ji。

应用叠加法计算截面的M值

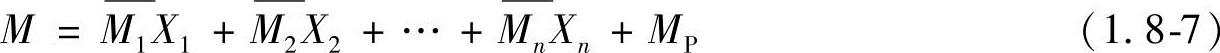
然后绘出最后弯矩图。根据弯矩图，再按各杆隔离体平衡条件，求出杆端剪力，绘制剪力图。根据剪力图，可用类似的方法绘出轴力图。