基准坐标系由三个基准平面、三个基准轴和原点组成,在基准坐标系中可以选择单个基准平面、基准轴或原点。基准坐标系可用来创建其他特征、约束草图和定位在一个装配中的组件等。下面通过图4.10.13所示的范例来说明创建基准坐标系的一般操作过程。选择下拉菜单命令,系统弹出图4.10.14所示的“基准CSYS”对话框。在建模过程中,经常需要对工作坐标系进行操作,以便于建模。图4.10.15 “CSYS”对话框◆ :通过两个矢量来创建一个坐标系。......
2023-10-17
当测区范围较小,把地球表面的一部分当做平面看待,所测得地面上点的位置或一系列点所构成的图形,可直接用相似而缩小的方法描绘到平面上去。但如果测区范围较大,由于存在较大的差异,不能用水平面代替球面。而作为大地坐标投影面的旋转椭球面又是一个“不可展”的曲面,不能简单地展成平面。这样就不能把地球很大一块地表面当做平面看待,必须将旋转椭球面上的点位换算到平面上,测量上称为地图投影。投影方法有多种,投影中可能存在角度、距离、面积三种变形,必须采用适当的投影方法来解决这个问题。测量工作中通常采用的是保证角度不变形的高斯投影方法。
为简单起见,把地球作为一个圆球看待,设想把一个平面卷成一个横圆柱,把它套在圆球外面。使横圆柱的轴心通过圆球的中心,把圆球面上一根子午线与横圆柱相切,即这条子午线与横圆柱重合,通常称它为“中央子午线”或称“轴子午线”。因为这种投影方法把地球分成若干范围不大的带进行投影,带的宽度一般分为经差6°、3°和1.5°等几种,简称为6°带、3°带和1.5°带。6°带是从0°子午线算起,以经度每差6°为一带,此带中间的一条子午线,就是此带的中央子午线或称轴子午线。以东半球来说,第一个6°投影带的中央子午线是东经3°,第二带的中央子午线是东经9°依此类推。对于3°投影带来说,它是从东经1°30′开始每隔3°为一个投影带,其第一带的中央子午线是东经3°,而第二带的中央子午线是东经6°,依此类推。图1-8表示两种投影的分带情况。中央子午线投影到横圆柱上是一条直线,把这条直线作为平面坐标系的纵坐标轴即x轴。所以中央子午线也称轴子午线。另外,扩大赤道面与横圆柱相交,这条交线必然与中央子午线相垂直。若将横圆柱沿母线切开并展平后,在圆柱面上(即投影面上)即形成两条互成正交的直线,如图1-9所示。这两条正交的直线相当于平面直角坐标系的纵横轴,故这种坐标系既是平面直角坐标系,又与大地坐标的经纬度发生联系,对大范围的测量工作也就适用了。这种方法是根据高斯创意并经克吕格改进的,因而通常称它为高斯-克吕格坐标系。
在高斯平面直角坐标系中,以每一带的中央子午线的投影为直角坐标系的纵轴x,向北为正,向南为负;以赤道的投影为直角坐标系的横轴y,向东为正,向西为负;两轴交点O为坐标原点。由于我国领土位于北半球,因此,x坐标值均为正值,y坐标可能有正有负,如图1-10所示,A、B两点的横坐标值分别为
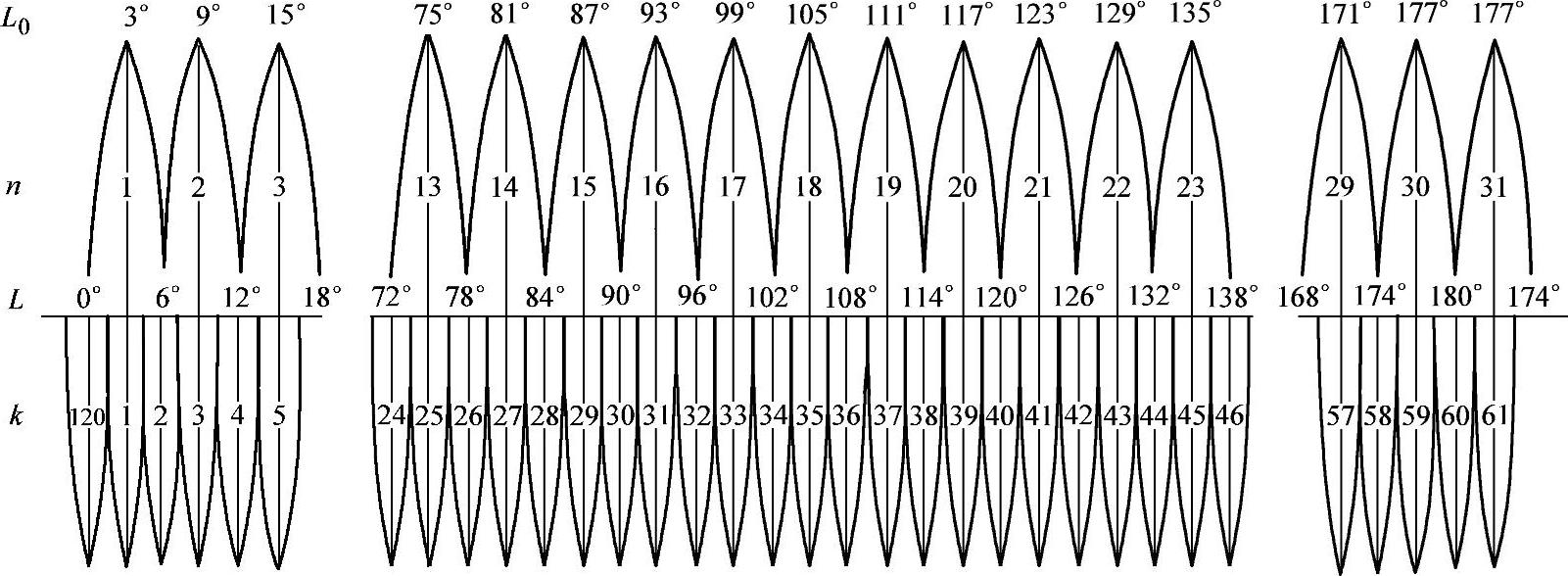
图1-8 两种投影的分带情况图
yA=+148680.54(m),yB=-134240.69(m)
为了避免出现负值,将每一带的坐标原点向西平移400km,即将横坐标值加400km,如图1-10所示,则A、B两点的横坐标值为
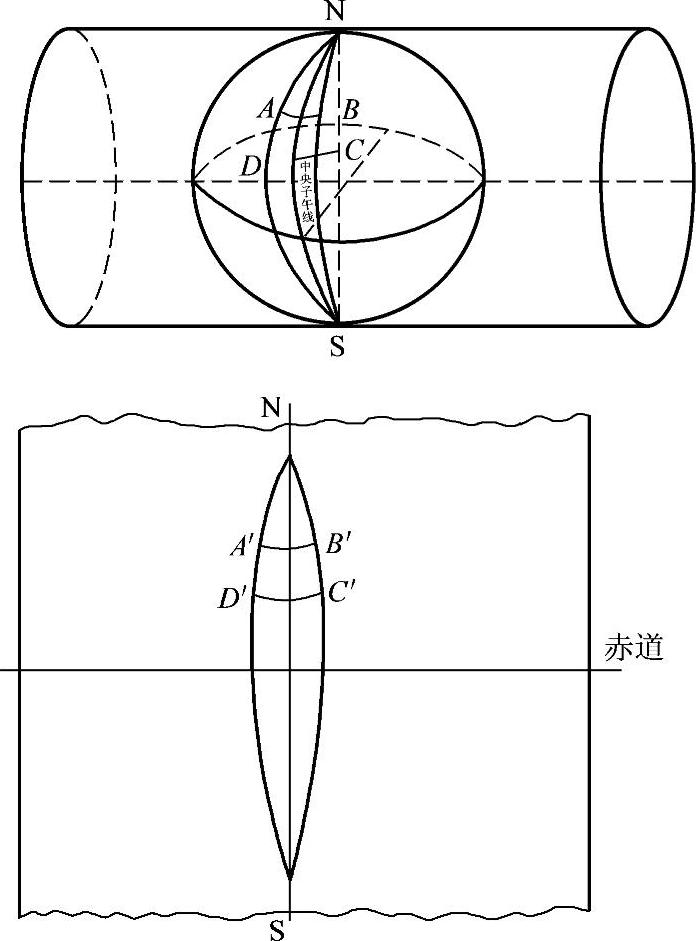
图1-9 圆柱面切割线正交直线
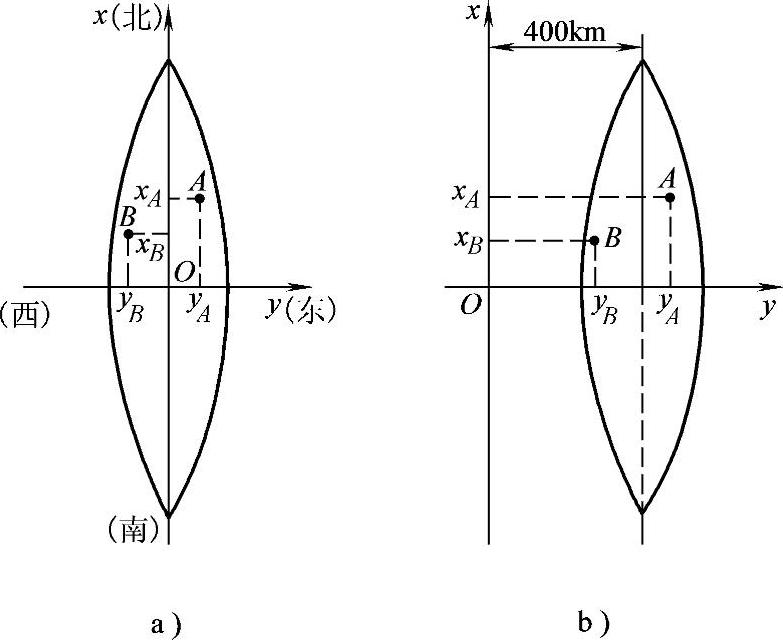
图1-10 直角坐标系
yA=400000+148680.54=548680.54(m)
yB=400000-134240.69=365759.31(m)
为了根据横坐标值能确定某一点位于哪一个6°(或3°)投影带内,再在横坐标前加注带号,例如,如果A点位于第22°带,则其横坐标值为
yA=22548680.54(m)
有关测量员的文章

基准坐标系由三个基准平面、三个基准轴和原点组成,在基准坐标系中可以选择单个基准平面、基准轴或原点。基准坐标系可用来创建其他特征、约束草图和定位在一个装配中的组件等。下面通过图4.10.13所示的范例来说明创建基准坐标系的一般操作过程。选择下拉菜单命令,系统弹出图4.10.14所示的“基准CSYS”对话框。在建模过程中,经常需要对工作坐标系进行操作,以便于建模。图4.10.15 “CSYS”对话框◆ :通过两个矢量来创建一个坐标系。......
2023-10-17

UG NX 9.0中有三种坐标系:绝对坐标系、工作坐标系和基准坐标系。系统用XC、YC和ZC表示工作坐标系的坐标。工作坐标系的XC-YC平面称为工作平面。可隐藏基准坐标系以及其单个组成部分。图2.6.1 工作坐标系图2.6.2 基准坐标系4.右手定则●常规的右手定则。......
2023-11-20

若标准方向为磁子午线方向,则称磁方位角,用Am表示。测量中常把直线前进方向称为正方向,反之称为反方向。如图10-13所示,设A为AB直线的起端,B为终端,则Aab为正真方位角,Aba为反真方位角。......
2023-08-20

图1-2-37手板葫芦2.手扳葫芦注意事项使用手扳葫芦时,起重量不准超过允许荷载,要按照标记的起重量使用。使用时不能任意的加长手柄,因手扳葫芦的起重量是有限的,两手扳力也有一定的大小,加长手柄会造成手扳葫芦的超载使用,致使部件损坏。手扳葫芦使用前要作全面的检查与测验,使用后要维护保养。......
2023-07-01

在定义模具坐标系前,首先要分析产品的结构、产品的脱模方向和分型面,然后再定义模具坐标系。定义模具坐标系之前,要先把产品坐标系调整到模具坐标系相应的位置,然后再用注塑模向导中定义模具坐标系的功能去定义。选择下拉菜单命令,系统弹出图14.3.1所示的“CSYS”对话框。对话框图14.3.4 定义后的模具坐标系锁定模具坐标系。在“模具CSYS”对话框中选择单选按钮,单击按钮,完成坐标系的锁定。......
2023-10-17

图4-8 感应式电能表的外形当用电设备工作时,电能表的铝盘将转动,带动计数机构在其机械式计度器窗口显示出读数。图4-10 单相智能电能表智能电能表的软件部分主要包括监控程序和接口管理程序两部分。图4-11 单相感应式电能表的接线图当三相三线负荷电流过大,无适当的三相三线直接接入式单相电能表可满足其要求时,应采用经电流互感器接线的计量方式,图4-12b为实物接线示意图。......
2023-08-18
相关推荐