大跨桥梁钢箱梁疲劳损伤分析方法

2023-08-26 理论教育版权反馈

【摘要】：大跨桥梁作为在复杂环境下长期服役的工程结构，其中的疲劳损伤累积过程是由多个因素耦合作用且跨尺度演化的过程。为模拟在此主要作用机理下的桥梁结构的疲劳损伤演化过程和剩余寿命，还须进一步发展模拟桥梁结构在服役荷载与极端荷载交互作用下的疲劳损伤跨尺度演化过程的多尺度有限元方法。当疲劳损伤演化处于长期缓慢累积过程时，如在结构服役的初期并且未遭受极端灾害荷载时，为提高疲劳损伤分析的效率，可在增量型平

大跨桥梁作为在复杂环境下长期服役的工程结构，其中的疲劳损伤累积过程是由多个因素耦合作用且跨尺度演化的过程。复杂环境作用除了如各种服役荷载、变温、腐蚀，还会有突发的极端荷载（如地震、台风、撞击等）。这些因素本身在桥梁服役期内对桥梁结构的作用强度、时长、方式等是难以准确预知的，同时这些因素引起的结构疲劳损伤演化机理也是十分复杂的，因此精确地预估由所有的因素共同作用引起的结构疲劳损伤状态及剩余疲劳寿命是十分困难的。但是，抓住对疲劳损伤演化过程起主要作用的因素进行模拟分析显然是在现有理论与研究条件下事半功倍的有效途径。对于大跨桥梁结构来说，疲劳损伤累积的主要作用因素就是服役荷载（交通荷载）与极端荷载（地震、台风等）交互作用下在结构易损局部发生的疲劳短裂纹与长裂纹扩展。对此，已建立的高、低周疲劳交互作用下的多尺度疲劳损伤模型可描述这一作用机理。为模拟在此主要作用机理下的桥梁结构的疲劳损伤演化过程和剩余寿命，还须进一步发展模拟桥梁结构在服役荷载与极端荷载交互作用下的疲劳损伤跨尺度演化过程的多尺度有限元方法。

目前对于大跨桥梁结构的有限元建模，通常采用结构单元，如用更小数量级的板、壳、实体单元来刻画结构真实几何细节及其力学与损伤特性，全局性的精细化建模将会带来高昂的计算代价，甚至导致计算无法进行。如要考虑结构易损局部疲劳累积的源头，在微观尺度建模去模拟短裂纹演化行为更是无法实现。因此为了对大跨桥梁结构进行考虑局部疲劳损伤演化过程的结构疲劳损伤分析，必须借鉴第七章的损伤多尺度跨层次模拟的思路，建立能够在微观尺度模拟易损局部发生的疲劳短裂纹成核与扩展行为，同时又能够模拟桥梁在服役荷载下的整体结构响应的多尺度有限元模型。桥梁结构的疲劳损伤累积主要发生于钢箱梁结构，而钢箱梁结构的几何与损伤蔓延特性与第七章的钢筋混凝土结构相差很大，因此这里不能直接搬用第七章的方法，须针对桥梁钢箱梁结构的几何特性与疲劳损伤特性进行专门的研究。

借鉴第七章的损伤多尺度跨层次模拟的思路，这里将大跨桥梁结构的计算区域离散为三类尺度与层次不同的子区域，分别对应于发生于材料、构件、结构三个层次上的疲劳损伤演化分析的需要：①第一类区域是描述短裂纹成核与扩展行为的微观分析子区域，这种区域一般位于结构易损局部的焊趾附近；②第二类区域是描述易损局部的关键构件几何细节以获得局部热点应力状态的宏观尺度上细化分析的子区域；③第三类区域是除了上述两类区域以外的所有其他区域，是用结构单元模拟的宏观区域。对于典型桥梁结构来说，上述三类区域的示意如图8.12所示。

pagenumber_ebook=243,pagenumber_book=233

图8.12　桥梁结构损伤多尺度跨层次建模示意图

在图8.12中的第三类区域，材料与结构的行为假设为连续的弹性响应；在第二类区域，由于热点应力分析是基于宏观尺度的连续均匀假设，其中的损伤必然只能使用连续损伤力学的基本概念与方法。因此，在第二类区域中的材料损伤本构由4.1.2节中的基本方程给出。在第一类区域，由于采用微观尺度下的模拟，金属材料在微观尺度下的疲劳损伤模拟采用由3.2节（高周疲劳损伤多尺度演化模型）或8.1节（高、低周疲劳交互作用下的疲劳损伤多尺度模型）中提出的方法。

在结构长期服役过程中，大部分时间是在正常服役荷载作用下，其中的疲劳损伤累积主要高周疲劳损伤演化。高周疲劳损伤演化的主要特点是应力幅度低、没有明显的塑性变形。在这种情况下，4.1.2节中的损伤本构方程（4－20）可以用循环应力应变关系表示为：

其中σij（i，j＝1，2，3）为Cauchy应力张量，εkl（i，j＝1，2，3）为应变张量，D（x，N）为疲劳损伤，x为空间位置，N当前疲劳加载的次数，Sijkl为初始弹性刚度张量，可表示为：

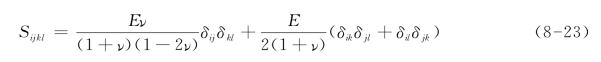
pagenumber_ebook=244,pagenumber_book=234

其中δ为克罗内克符号 pagenumber_ebook=244,pagenumber_book=234 ，E为弹性模量，ν为泊松比。

高周疲劳损伤演化的特点是，在单个应力循环中产生的疲劳损伤增量非常小，需要足够多次的循环才能使得发生显著的疲劳损伤演化从而改变结构的响应（即导致结构性能劣化、产生损伤附加变形）。由此可见，在进行结构疲劳损伤有限元分析去模拟结构高周疲劳损伤演化过程中，如果对每个应力循环都进行计算（Cycle－by－Cycle），通常会超出计算能力，是不可行的，同时也是没有必要的。为了降低计算代价，加速疲劳损伤演化过程的模拟，经常采用块循环（Block cycle jump）技术，即将数个应力循环封装成一个块循环步，如将ΔNi作为第i个块循环步的增量。如采用向后欧拉积分方法，则如下计算块循环产生的疲劳损伤增量：

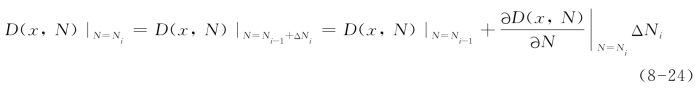
pagenumber_ebook=244,pagenumber_book=234

其中Ni为第i个块循环次数。这里采用半解耦的方法进行疲劳损伤计算，即只在疲劳损伤本构关系中引入损伤，而在平衡方程中则忽略当前损伤增量对应力增量的影响。

当前应变增量可表示为：

其中，n表示当前的时间增量步。

根据所获得的应变增量和上一荷载步所计算得到的损伤变量来进行当前应力更新：

当每一块循环步计算完成后，利用方程（8－24）进行一次疲劳损伤变量的更新：

pagenumber_ebook=245,pagenumber_book=235

其中的疲劳损伤演化方程由3.2节中给出的高周疲劳损伤多尺度演化模型或8.1节中给出的高、低周疲劳交互作用下的疲劳损伤多尺度模型中的相关方程给出。采用哪种损伤演化模型由造成疲劳损伤演化的荷载（应力）循环是属于高周还是高、低周共存来决定。

连续损伤力学中的疲劳损伤模型是基于应力或者应变来分析疲劳损伤的，属于宏观连续力学的范畴，只有在宏观尺度上将材料假定为连续均匀时才是有效的。而在这里的微观分析区域需要考虑材料内部非均匀的微观结构及其中的缺陷导致的微裂纹成核和扩展过程，单纯利用宏观疲劳损伤模型来模拟疲劳损伤演化的方法不再适用。所以在这里所发展方法中的微观分析区域必须选择3.2节的高周疲劳损伤多尺度演化模型或8.1节的高、低周疲劳交互作用下的疲劳损伤多尺度模型，同时须采用基于钢材微观构造图像的微裂纹成核与扩展行为模拟方法来模拟微观尺度上短（或长、短）裂纹群体演化的过程，利用所建立的多尺度疲劳损伤模型去获得描述微观分析区域的裂纹成核与扩展行为的参数。

当疲劳损伤演化处于长期缓慢累积过程时，如在结构服役的初期并且未遭受极端灾害荷载时，为提高疲劳损伤分析的效率，可在增量型平衡方程求解过程中忽略当前增量步中的损伤演化进程。为减少由此可能带来的误差，须严格控制荷载增量步长。为此在疲劳损伤演化过程模拟中耦合了自动确定荷载步长时的循环加载次数增量ΔNi的算法，去严格控制每一个单元中的损伤增量，这里ΔNi通过下述方程来获得：

pagenumber_ebook=245,pagenumber_book=235

其中ΔDi为当前荷载步内所有单元所允许的最大损伤增量，D（e，Ni）为某一单元的当前损伤量，为由该单元所计算得到的当前荷载步所最大允许的循环加载次数的增量。

必须指出的是，在建立大跨桥梁结构疲劳损伤多尺度模型之前，首先需要在整个计算区域中确定三个不同尺度与层次的子区域的划分。为此需要首先针对桥梁结构整体的梁单元模型进行结构内力分析，确定结构易损构件及其初始缺陷位置，然后在易损局部植入包含构件具体构造细节的细化分析模型；针对该模型再进行疲劳损伤演化的初步模拟，在细化模型中找到易损细节及其应力集中区域，植入微观尺度疲劳损伤模型；最后针对包含微观尺度模型的多尺度跨层次的大跨桥梁模型进行多尺度跨层次的疲劳损伤演化过程模拟。上述分析过程的具体做法将会结合以下的昂船洲大桥钢箱梁结构疲劳损伤演化的多尺度跨层次数值模拟算例进行阐述。

大跨桥梁钢箱梁疲劳损伤分析方法

相关推荐